Petri网在架空电缆无人机巡检方面的研究

孙 霞 张 洁 赵厚群 张坤乾 缪玉婷

（安徽理工大学电气与信息工程学院 安徽淮南 232001）

随着航空工业领域的快速发展，无人机作为巡检装备之一。因其具有体积小、成本低、使用方便、技术简单成熟等特点[1-2]，逐渐在电力设备巡检中得到认可。目前已使用于电力系统维护的方方面面，例如，将无人机用于输电线路的巡检[3]；针对光伏电站体积较大，运维压力等问题，提出一种基于光伏电站的无人机智能巡检完整技术路线[4]。利用无人机巡检，可以及时发现缺陷，弥补传统巡检的不足，提高对电气设备的巡检质量，减轻运维人员的工作压力。Petri网作为一种优秀的系统建模和分析工具，可应用于多种场景，在处理实际问题时，可用Petri网的相应性质和行为轮廓对系统进行建模和优化。物联网技术已在各个领域中得到广泛应用，本文将物联网技术与无人机巡检相结合，提出架空电缆无人机巡检的优化模型。

一、基本概念

（一）有向网。若满足以下3个条件的三元组N=(S,T;F)就称为有向网，简称网。

①S∪T≠∅ΛS∩T=∅。

②F⊆S×T∪T×S。

③dom(F)∪ cod(F)=S∪ T。

dom(F)={x|∃y(x,y)∈ F}；

cod(F)={y|∃x:(x,y)∈ F}。S和T是两个不相交的集合。其中S元素称为库所(place)，T元素称为变迁(transition)，F是网N的流关系(flow ralation)，“×”表示笛卡尔积。Petri网规则：如果某一个变迁的所有前驱库所都有托肯，则这个变迁满足发射条件。变迁发射时，从它所有的前驱库所里分别取出1个托肯，同时往它所有的后继库所里面分别放置1个托肯，以此类推。

（二）Petri网系统。Σ=（S,T;F,K,W,M0）是Petri网系统，其中K是N上的容量函数（S元素的容量函数），W是N上的权函数（资源消耗或产生的量），应满足

①N=（S,T;F）为Σ的基网，为有向网。

②M0是容量函数K允许的标识（初始标识）。

(1)若变迁t∈T，则t在M有发生权的条件是∀s=.t:M(s)≥ 1，则称t在M使能，记作M[t＞1；

(2)若t在M有发生权，则t可以发生并将M改为新的表示M'，记作M[t＞M'，则有

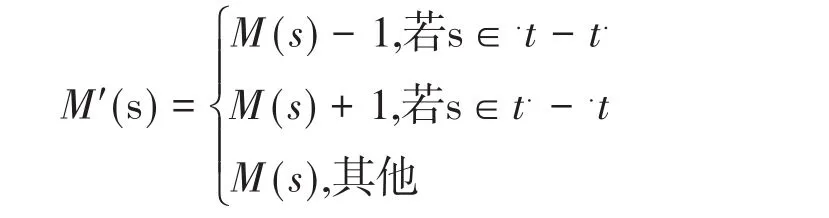
（三）行为轮廓。（N,M0）是一个网，初始标识M0。将所有关系的集合称为网系统的行为轮廓[5]，记作BP={→,→-1,+,||}对任给的变迁（t1,t2）∈（TXT）满足下列关系：

（1）若t1＞t2且t2≯t1，则称严格序关系，记作t1＞→t2；

（2）若t1≯t2且t2＞t1，则称严格逆序关系，记作t1→-1t2；

（3）若t1≯t2且t2≯t1，则称排他关系，记作t1+t2；

（4）若t1＞t2且t2＞t1，则称交叉序关系，记作t1||t2。

（四）结构性质。网系统Σ=（S,T;F,W,M0），其结构性质是由网系统的静态结构决定的，与初始标识无关，网系统的静态结构用（S,T;F,W）表示。

（1）关联矩阵：矩阵A=(Aij)为网系统Σ=（S,T;F,W,M0）的关联矩阵，A以S为行序标集，以T为列序标集，其i行j列的矩阵元素aij=W'（tj,si）-W'（si,tj）。其中W'由W扩展而来，若（x,y）∈F，则W'(x,y)=W(x,y)；若(x,y)∉F，则W'(x,y)=0。

（2）状态方程M=M0+A × τT，其中，τ为任一T_向量，M0和M分别是标识的S_向量。

①若T_向量τ满足M0=M0+A×τT，则称τ为Σ的T_不变量，若τ为Σ的T_不变量，则A× τT= θST,其中，θs是分量全为0的S_向量。

②若S_向量σ满足σ ×A=θT，则σ称为Σ的S_不变量，其中θT是分量全为0的T_向量。

二、优化前架空电缆无人机巡检Petri模型

无人机巡检是目前最受关注的问题之一，本文是借助无人机通过搭载的视频设备，对架空电缆进行监测、数据采集。运维人员可以借助无人机进行人工无法实现的、危险的以及重复的架空电缆的运维工作。下面利用Petri网对架空电缆无人机巡检进行建模分析。

图1为架空电缆无人机巡检流程的Petri网模型图，图中P0库所中的token代表巡检无人机，运维人员对无人机进行检查、试飞后，无人机搭载机载设备，按照规划的飞行路线对架空电缆进行巡检。T0、T1、T2发生后，无人机对周围环境进行采集，T3和T5是排他关系，若拍摄画面显示无异常，则T3、T4发生，继续或结束巡检。若拍摄画面有异常，T5发生，T6和T9是并发关系，可同时发生。例如发现鸟窝，T6-T8发生；发现有树枝遮挡，T9-T11发生，运维人员接收到画面立刻前去清理，清理完毕后，T4发生，继续或结束巡检。架空电缆无人机巡检流程的Petri网模型各变迁符号及意义文字说明见表1。

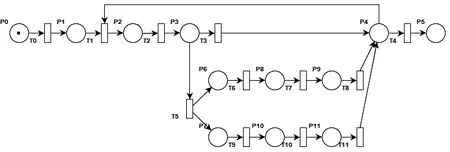
图1 优化前架空电缆无人机巡检Petri网模型

表1 优化前架空电缆无人机巡检流程的Petri网模型各变迁符号及意义文字说明

三、优化后架空电缆无人机巡检Petri模型

优化前的无人机巡检方式单一，且只能依靠设备所拍摄的画面来监测架空电缆是否出现故障等问题。相比于优化前的架空电缆无人机巡检，优化后的无人机巡检增加了红外感应设备，以实现对架空电缆的温度监测。不同于可见光的人感应，红外因其具有较强的辐射能力，可以监测到在可见光波段无法监测的特定目标[6]。该设备是由红外感应模块、微处理器模块、电源模块和LoRa通信模块组成。LoRa传输技术满足低功耗、远距离传输，信号灵敏、响应速度高且数据传输的抗干扰能力强[7-8]。整体流程为：红外感应模块对架空电缆环境数据进行采集，通过LoRa技术将数据传输至监测中心。由此对架空电缆无人机巡检进行优化，增添相关活动变迁和行为轮廓，构建成新的架空电缆无人机巡检Petri网模型。图2则是优化后的架空电缆无人机巡检的Petri网模型。

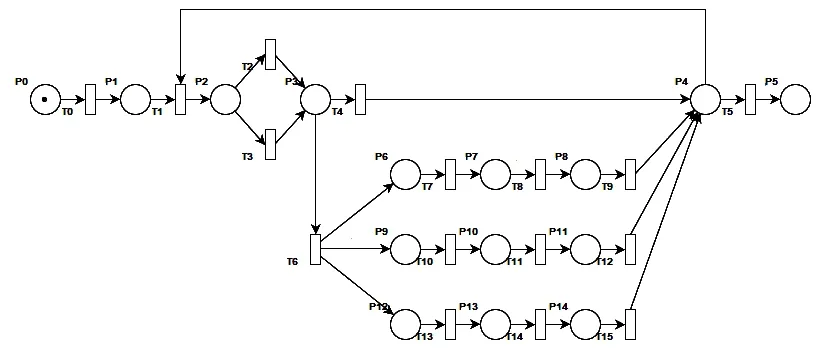
图2 优化后架空电缆无人机巡检petri网模型

图中库所P0的token代表无人机。运维人员操控无人机起飞后开始巡检，图中T2、T3是并发关系，二者同时发生，视频设备拍摄有无异常画面，红外感应设备采集数据，通过阈值对比，监测电缆是否存在异常高温可能。T4和T6是一对排他关系，无异常，T4发生，结束巡检。若存在异常，T6发生，例如若红外感应设备所监测电缆环境数值超过设定阈值，T13发生，数据通过LoRa的射频芯片进行传输处理，将数据上传至监测中心，运维人员及时锁定发生异常方位，并前往处理，T14发生，检修完毕（T15）后，继续巡检或结束巡检（T5）。优化后架空电缆无人机巡检流程的Petri网模型各变迁符号及意义文字说明见表2。

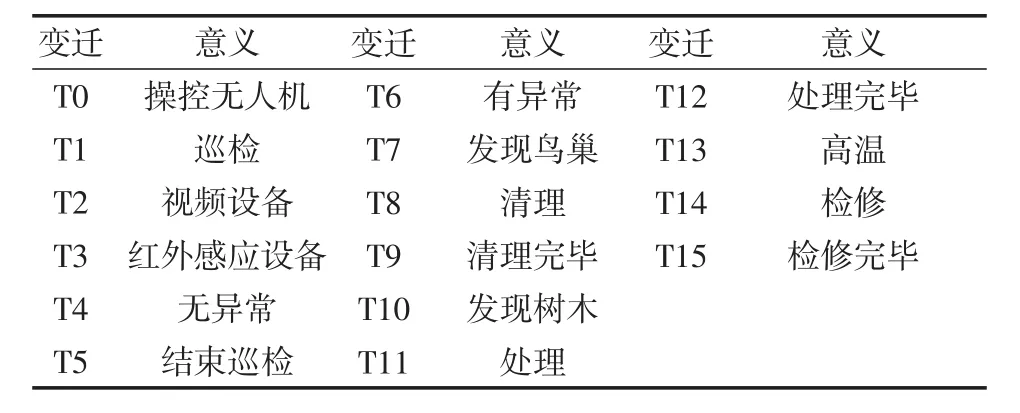
表2 优化后架空电缆无人机巡检流程Petri网模型各变迁符号及意义文字说明

四、优化后架空电缆无人机巡检Petri网性能分析与验证

（一）性质分析。Petri网的一个标识可以表示成一个m维非负整数向量。Petri网的结构也可以用一个矩阵来表示，即引入线性代数的方法对Petri网的性质进行分析[9]。通过分析其静态性质，可验证出该模型的结构稳定性。

架空电缆无人机巡检的Petri网的静态性质是由关联矩阵A、输入矩阵B、输出矩阵C表示，三者的关系式为A=B-C。矩阵中S为行标集，T为列标集。

1.输入矩阵。输入矩阵的矩阵元素用bij表示，当变迁发生时，库所中产生token，初始库所中只消耗token。

2.输出矩阵。输出矩阵的矩阵元素用cij表示，当变迁发生时，会消耗token，架空电缆无人机巡检的Petri网的输出矩阵C如下所示。

3.关联矩阵。是对网系统的结构描述，与初始标识无关。关联矩阵的矩阵元素用aij表示，aij是变迁tj发生一次对si所含token数量的改变，发生变迁时，会产生或是消耗token，产生用正数，消耗用负数表示。行对应着库所与相应变迁集间的关系，列对应着变迁与相应库所集间的关系。架空电缆无人机巡检的Petri网的关联矩阵A如下所示。

根据架空电缆无人机巡检的Petri网模型的关联矩阵，由公式ATX=θT与AY=θS的可得出通解X和Y，即S_不变量和T_不变量，由后者可解出矩阵的通解YT为：

YT=(0 0-1 1 0 0 0 0 0 0 0 0 0 0 0 0)。

由矩阵的通解可知，分量1代表token从库所流至变迁，分量-1代表token从变迁流至库所。变迁发生不会改变库所中的token数，故架空电缆无人机巡检的Petri网模型的流通路径是固定的。因此，该检测方式的Petri网结构是静态稳定的、可达的。

（二）仿真实验验证。为检验优化后的架空电缆无人机巡检Petri网模型的正确性与可达性，在Petri网分析软件PIPE中绘制模型图，利用State Space Analysis函数，对优化后的模型进行验证。运行结果图如图3所示。结果表明，优化后的模型是可达的。

图3 PIPE模型仿真检验图

五、结语

通过对传统架空电缆无人机巡检Petri网模型的分析，在此基础上，增加红外感应设备，应用物联网技术对电缆环境数据进行无线传输，建模优化架空电缆无人机巡检方式，对其Petri网的静态结构分析可达性与准确性，并在PIPE软件中得到验证。优化后的架空电缆无人机巡检方式，可减轻运维人员的工作强度，能够使得运维人员能够快速地发现故障点并及时检修或处理。