基于一种扩展模糊Petri网的列车运行晚点致因建模分析

王诗慧，李孝忠

(天津科技大学计算机科学与信息工程学院，天津 300222)

基于一种扩展模糊Petri网的列车运行晚点致因建模分析

王诗慧，李孝忠

(天津科技大学计算机科学与信息工程学院，天津 300222)

针对目前我国列车运行晚点较严重的问题，提出一种扩展的模糊Petri网(extended fuuzy Petri net，EFPN)，并以对列车正点运行有重大影响的主要因素为基础，模拟给出其因果关系，建立了基于EFPN的列车运行致因的分析模型，利用EFPN推理算法分析计算模型中某个致因因素导致列车运行晚点的真实度，真实度最高的致因因素则是导致列车运行晚点的最主要因素．实例分析表明，EFPN模型能够体现各因素之间的逻辑关系，通过定量分析可得到导致列车运行晚点的主要原因．

列车晚点；EFPN；致因分析；真实度

随着国民经济迅速发展，铁路现代化建设进程正逐步加快．但与此同时，铁路干线运输密度大、铁路季节性的运能紧张、现有技术装备水平低、路网分布不均等弊端也使得我国铁路运输产业面临着空前挑战[1]．其中，铁路运输能力和运量的矛盾日渐突出，列车晚点现象时有发生．列车运行秩序不好、晚点现象严重，不仅给旅客带来许多不便，也会给铁路工作人员带来非常大的工作压力，更有损铁路声誉和国家形象．因此，对列车运行晚点致因的研究是非常重要的．

文献[2]分析了铁路旅客列车晚点的原因，并强调保证列车正点运行的重要性和紧要性．文献[3]在分析列车晚点分类和晚点传播特点的基础上，从控制直接影响列车正点率影响因素和控制晚点传播范围入手，针对各影响因素，提出提高高速列车正点率的各项措施及调度部门对晚点列车的调整策略和调整方法．但上述研究都是定性分析列车晚点原因，是对对象性质特点的概括，是抽象的分析，不能依靠数据来具体地定量分析并给出直观的数据结果．

Petri网普遍被认为是描述具有并行或并发行为的系统的一种好工具，在有关描述和分析并行系统的各种问题中有着广泛的应用[4–5]，传统的Petri网无法处理一些不明确或模糊的信息，因此模糊Petri网(fuzzy Petri net，FPN)应运而生[6]．FPN以模糊产生式规则为基础，它既有一般Petri网的图形描述能力，又可以表现出知识库系统中规则之间的结构化特性，并在故障诊断、知识推理等方面得到一定的应用[7–8]．

本文在现有对列车晚点原因定性研究的基础上，提出一种扩展的模糊Petri网(extended fuzzy Petri net，EFPN)，利用EFPN在分析影响列车正点运行的主要因素的基础上进行建模，通过EFPN推理算法定量分析导致列车晚点的最主要因素．

1 模糊Petri网基础知识

1.1 基本模糊Petri网

基本模糊Petri网是一个六元组

式中：P={p1,p2,…,pn}是库所节点的有限集合；T={t1, t2,…,tm}是变迁节点的有限集合；I是输入函数，即从库所集到变迁集的映射P× T→{0,1}，若I(p，t)＝1，表明pi是ti的输入库所，否则不是，I(ti)表示变迁ti的输入库所集合；O是输出函数，即从变迁集到库所集的映射P× T→{0,1}，若O(p，t)＝1，表明pi是ti的输出库所，否则不是，O(ti)表示变迁ti的输出库所集合；α是库所到该库所中托肯的映射，α(pi)＝αi表示库所pi的托肯值是αi；f表示每个变迁对应1个0到1之间的实数，即T→[0,1]，它是变迁到其置信度(CF)的映射，f(ti)＝μi表示变迁ti的置信度是μi．

既然FPN能够将传统Petri网的三元结构扩展到六元，那么在FPN的基础上也可进行扩展，形成各种类型的FPN的网结构，比较常用的是用于知识表示的模糊Petri网．

1.2 模糊Petri网与知识表达

对于1个基于规则的系统，其产生式规则可以用相应的模糊Petri网模型来表示．在知识表示中，模糊产生式规则就是对于两个或多个命题之间关系的描述．

通常用于知识表示的产生式规则有多个，对于每个规则都有一定的含义，如果用模糊产生式规则来表示，规则的基本定义是

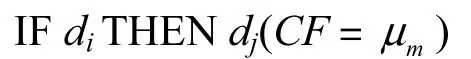
其中：di和dj代表命题，其值是0到1的实数；μm是规则的置信度(CF)，μm∈[0,1]，μm越接近1，命题就越真实，越值得被相信．模糊产生式规则一般有图1所示的3种类型，对应的规则为

规则1：IF diTHEN dj(CF＝mμ)

规则2：IF diOR djTHEN dk(CF＝mμ，nμ)

规则3：IF diAND djTHEN dk(CF＝mμ)

图1 3种模糊产生式规则的FPNFig. 1 FPN of three kinds of fuzzy production rules

由以上3种模糊产生式规则的FPN看出，如果图中各库所表示产生式规则中的各命题，那么图中的每个有向弧就可以表示1个规则，这样就可以将知识表示用FPN来进行描述，即扩展的模糊Petri网(EFPN)．

1.3 EFPN

定义1 EFPN是一个十元组结构

其中：P={p1, p2,…,pn}是库所节点的有限集合；T={t1, t2,…,tm}是变迁节点的有限集合；F为有向弧集合，F⊆(P× T)∪(T×P)；D={d1, d2,…dn}是有限命题的集合，P∩T∩D=∅，P∪T≠∅，且|P|=|D|；f：T→[0,1]是函数，表示变迁所对应的推理规则的置信度；α：P→[0,1]，是库所P的关联函数，α(pi)＝αi表示该库所对应的命题的真值(真实度)为αi，αi∈[0，1]，i＝1，2，…，n；β：P→D是库所到与之对应的命题之间的关系，β,(pi)＝di表示库所pi可以代表与之相对应的命题di，而pi的托肯值就是di的真值，也就是说，如果α(pi)＝αi，且β(pi)＝di，则命题di的真值为αi；λ：T→[0,1]是变迁的阈值映射，表示对命题的实际支持度(真实度)的最低要求；L是长度为2的数组，即有2个元素，用来判断库所是否被查看或标注，第1个元素是数字0(未被查看)或库所p∈P的记号p，第2个元素是数字0(未被标注)或α(p)，比如库所pi和库所pj是相邻库所(见定义3)，且L(pj)＝[pi，α(pj)]，则说明库所pj已被查看并标注；M0是模糊Petri网的初始标识，用托肯来表示，若库所pi∈P的命题成立，则M (pi)＝1，否则M (pi)＝0.

定义2 变迁运行规则

(1)变迁ti使能的充分条件是：∨pi∈⋅ti，M( pi)×α(pi)≥λi；

(2)变迁ti使能的必要条件是：变迁ti使能即被触发，ti触发后会产生新的标志M′，记作M[ti＞M′，其新标志的产生规则为

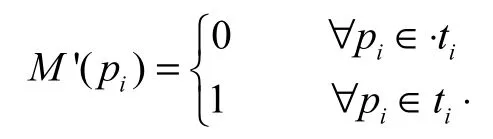
在上述定义的模糊Petri网中，1个变迁t及其前后集(⋅t和t⋅)中的各个库所模拟1条模糊推理规则，其中⋅t中的库所代表前提条件，t⋅的库所代表推理结果.

定义3 相邻库所

若t为EFPN中的变迁，pi和pj为EFPN中的库所，满足pi∈⋅tj，pj∈tj⋅，则pi和pj就是相邻库所．

1.4 EFPN的推理规则

(1)IF diTHEN dj(CF＝μk)

其中：di和dj代表命题，且α(pi)＝αi，即命题di的真实度是αi；变迁tk用来表示命题之间的关系，也即规则，其置信度是μk．当ti触发后命题dj的真实度α(pj)＝α(pi)×μk，dj对应的库所pj上的标注为L(pj)＝[pi，α(pj)]．

(2)IF d1OR d2…OR diTHEN da( CF=μi)

其中：d1、d2、…、di、da是命题．当变迁ti触发后，命题da的真实度α(pa)=max[α(p1)×μi, α(p2)×μi,…, α(pi)×μi]da对应的库所pa上的标注L(pa)＝[pi，α(pa)]．

(3)IF d1AND d2…AND diTHEN da(CF=μi)其中：d1、d2、…、di、da都是命题．当变迁ti触发后，命题da的真实度是α(pa)=min[α(p1),α(p2),…,α(pi)]×μi, da对应的库所pa上的标注L(pa)＝[pi，α(pa)]．

2 模型的建立与分析

2.1 EFPN模型的推理算法

设库所pi表示影响列车正点运行的主要因素，各个主要因素的状态由库所对应的命题di表示，其真实度为α(pi)．若目标库所表示列车已晚点，起始库所就是列车运行过程中影响列车正点运行的致因因素，变迁ti表示事件，其置信度μi表示该事件发生的可能性，以变迁的触发表示推理的进行．据此能够得到相应列车运行晚点的致因EFPN模型．本文基于正向推理方法[9–10]，每条规则从第1个库所到目标库所进行推理计算，这条规则经过的库所上都会设有1个标注L，当推理至目标库所时，再根据每条规则上的库所的标注值回溯至第1个库所，进而得到致因因素．假设EFPN模型中有n个库所，m个变迁，其推理算法的具体步骤是：

(1)若库所pi∈P对应于列车晚点的致因因素，则M (pi)＝1；否则M (pi)＝0，其中i＝1，2，…，n．

(2)单独设置1个库所p0，对于所有库所pi，如果M(pi)＝1，则在p0和pi之间添加变迁t，使得⋅t＝p0，t⋅＝pi，α(p0)＝1，μ(t)＝α(p0)，λ(t)＝α(p0).

(3)令L(p0)＝[0，1]，则p0是已经被标注但并未被查看的库所．

(4)根据被标注的先后次序，取1个已被标注但还未被查看的库所pi，对与其相邻的所有库所pj，若pi∈⋅tij,pj∈tij⋅，则

若α(pi)＞λ(tij)，则令L(pj)＝[pi，α(pj)]，即将库所pj标注，其中，α(pj)＝α(pi)×μ(tij)；

若|⋅tij|＝l，l≥2，当所有α(pi)＞λ(tij)，i＝1，2，…，l时，则给L(pj)赋值，即L(pj)＝[pi，α(pj)]，其中α(pj)＝min[α(p1)，α(p2)，…，α(pj)]×μ(tij)；

若α(pi)≤λ(tij)，则不对库所pj进行标注，即L(pi)＝[0，α(pi)]；

若库所pj已经被标注，则将新计算得到的L值L′(pj)和以前的L值L(pj)中的第2个元素进行比较，即比较α′(pj)与α(pj)，结果取较大的值．

(5)若库所pi已被查看，则重复步骤(4)，直至所有库所都已经被查看．

(6)按照目标库所的L值的第1个元素反向追踪找到主要路径，即令目标库所对应的命题的真实度最高的路径，该路径上的各因素，也就是路径上的库所，便是导致列车晚点的主要因素．

2.2 模型建立

首先从人为因素、列车、设备、线路和天气5个方面考虑，选择对严重影响列车正点运行的主要因素，建立基于EFPN的列车晚点致因分析的模型．人为因素方面包括内部人为因素和外部人为因素，内部人为因素主要包括驾驶员的受教育程度、对列车操控的熟练程度、驾驶员的时间观念及铁路内部人员矛盾等；外部人为因素主要包括列车严重超员、闲杂人员侵入铁道线路．在列车方面，列车“套跑”、列车故障是主要因素．在设备方面，通信设备故障是主要因素．在线路方面，车流情况、线路枢纽能力、线路施工情况等线路信息为主要因素．在天气因素方面，暴风雪等恶劣的天气导致视线能见度低、路况差等是导致列车运行晚点的主要因素．综合考虑上述各方面因素，建立基于EFPN的列车晚点致因模型，如图2所示．EFPN模型的库所和命题的含义分别见表1和表2．

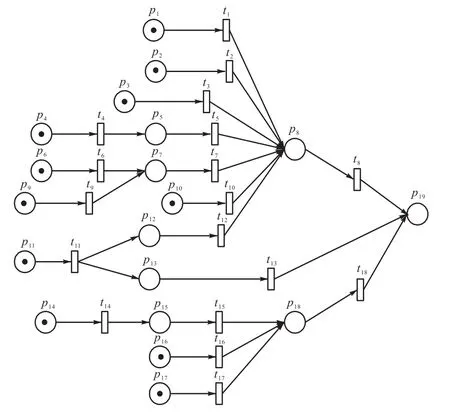
图2 基于EFPN的列车晚点致因模型Fig. 2 Model of causes of train delays based on EFPN

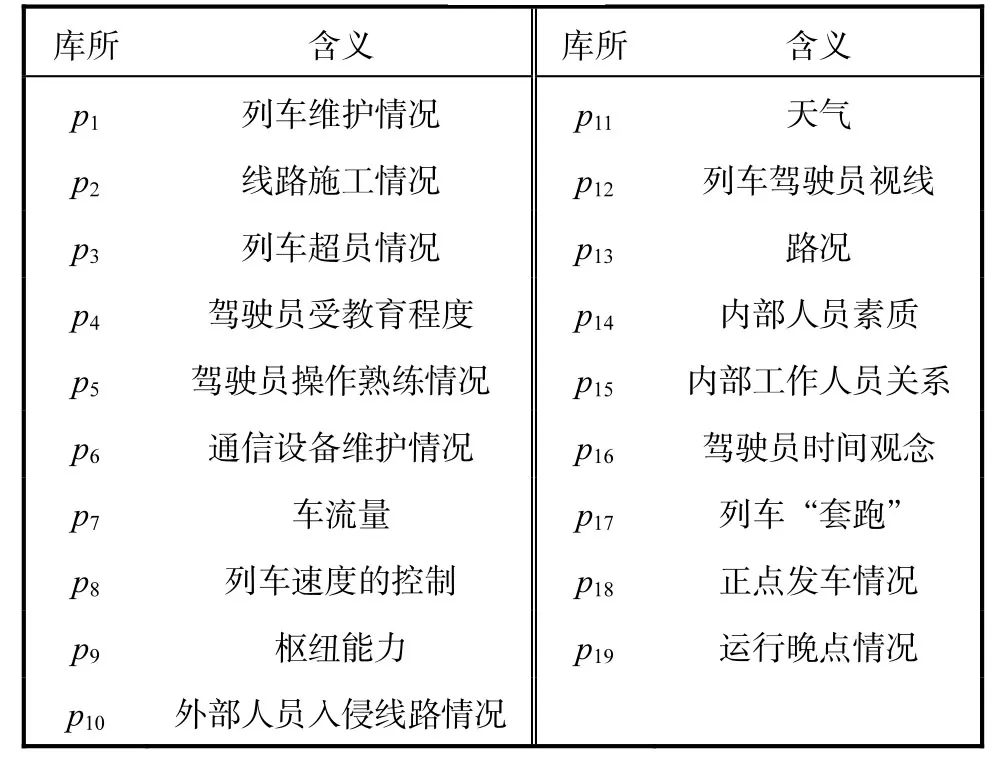
表1 EFPN模型库所含义Tab. 1 Meaning of places in EFPN

表2 EFPN模型命题含义Tab. 2 Meaning of proposition in EFPN

在基于EFPN的列车晚点致因模型中，变迁的具体含义表示1个推理的过程，比如：若pa∈⋅ti，pb∈ti⋅，则变迁ti可以理解为：如果与库所pa相对应的命题da成立，那么与库所pb相对应的命题也成立．图2中变迁t16的含义可以这样理解：如果列车驾驶员的时间观念差，则导致列车未能正点发车，列车将不能完全按照运行图行驶．

2.3 模型分析

根据2.1节EFPN模型的推理算法对图2进行计算分析，该模型的致因因素对应的库所为p1、p2、p3、p4、p6、p9、p11、p14、p16、p17．假设根据该趟列车的实际情况，通过专家打分方法对这些库所中命题的真实程度进行推断，最终得到各个命题的真实度为α,(p1)＝0.10，α,(p2)＝0.76，α,(p3)＝0.93，α,(p4)＝0.66，α,(p6)＝0.84，α,(p9)＝0.98，α,(p10)＝0.85，α,(p11)＝0.85，α,(p14)＝0.50，α,(p16)＝0.74，α,(p17)＝0.30，各个变迁的置信度为μ8(t1)＝0.94，μ8(t2)＝0.94，μ8(t3)＝0.90，μ5(t4)＝0.88，μ8(t5)＝0.87，μ7(t6)＝0.90，μ8(t7)＝0.91，μ19(t8)＝0.98，μ7(t9)＝0.98，μ8(t10)＝0.91，μ12(t11)＝0.90，μ13(t11)＝0.95，μ8(t12)＝0.89，μ19(t13)＝0.94，μ15(t14)＝0.83，μ18(t15)＝0.85，μ18(t16)＝0.87，μ18(t17)＝0.88，μ19(t18)＝0.96，其中μ的下标表示其对应的变迁发生后的下一个库所序号，例如：8μ(t1)表示变迁t1发生后到库所p8方向的置信度．设各个变迁的阈值iλ＝0.61，i＝1，2，…，13．单独设置库所p0，并在p0与p1、p2、p3、p4、p6、p9、p11、p14、p16、p17之间分别添加相应的变迁及有向弧，通过EFPN模型的推理算法，具体计算步骤如下：

(1)在所有托肯为1的库所中排除所有α,(pi)小于阈值iλ的库所．

(2)t2发生时α,(p8)＝α,(p2)×μ8(t2)＝0.76×0.94＝0.714,4，则L(p8)＝[p2，α,(p8)]＝[p2，0.714,4]．

(3)t3发生时α,(p8)＝α,(p3)×μ8(t3)＝0.93×0.90＝0.837，则L(p8)＝[p3，α,(p8)]＝[p3，0.837]．

(4)t4发生时α,(p5)＝α,(p4)×μ5(t4)＝0.66×0.88＝0.580,8，由于α,(p5)＜λ5＝0.61，t5不会使能．

(5)t6发生时α,(p7)＝α,(p6)×μ7(t6)＝0.84×0.90＝0.756，则L(p7)＝[p6，α,(p7)]＝[p6，0.756]．

(6)t9发生时α,(p7)＝α,(p9)×μ7(t9)＝0.98×0.98＝0.960,4，则L(p7)＝[p9，α,(p7)]＝[p9，0.960,4]．此时所有到达p7的情况已经计算，取所有L(p7)的第2个元素值最大者，即[p9，0.960,4]．

(7)t7发生时α,(p8)＝α,(p7)×μ8(t7)＝0.960,4× 0.91＝0.874,0，则L(p8)＝[p7，0.874,0]．

(8)t10发生时α,(p8)＝α,(p10)×μ8(t10)＝0.85× 0.91＝0.773,5，则L(p8)＝[p10，0.773,5]．

(9)t11发生时α,(p12)＝α,(p11)×μ12(t11)＝0.85× 0.9＝0.765，则L(p12)＝[p11，0.765]．

(10)t12发生时α,(p8)＝α,(p12)×μ8(t12)＝0.765× 0.89＝0.680,9，则L(p8)＝[p12，0.680,9]．此时所有到达p8的情况已经计算，取所有L(p8)的第2个元素值最大者，即[p7，0.874,0]．

(11)t8发生时α,(p19)＝α,(p8)×μ19(t8)＝0.874,0× 0.98＝0.856,5，则L(p19)＝[p8，0.856,5]．

(12)t11发生时α,(p13)＝α(p11)×μ13(t11)＝0.85× 0.95＝0.807,5，则L(p13)＝[p11，0.807,5]．

(13)t13发生时α,(p19)＝α,(p13)×μ19(t13)＝0.807,5× 0.94＝0.759,1，则L(p13)＝[p13，0.759,1]．

(14)t16发生时α,(p18)＝α,(p16)×μ18(t16)＝0.74× 0.87＝0.643,8，则L(p18)＝[p16，0.643,8]．

(15)t18发生时α,(p19)＝α,(p18)×μ19(t18)＝0.643,8× 0.96＝0.618,0，则L(p19)＝[p18，0.618,0]．

此时所有到达p19的情况已经计算，取所有L(p19)的第2个元素值最大者，即[p8，0.856,5]．此时已达目标库所，根据其L值的第1个元素依次回溯的结果为p0、p9、p7、p8、p19，去掉临时加入的库所p0得到该实例中列车晚点的致因因素就是p9，即由于枢纽能力差使得车流复杂，进而导致列车运行晚点的真实度约等于0.856，它是所有致因因素中导致列车晚点真实度最高的因素．那么接下来就可以通过提高枢纽能力的方法来降低列车晚点频率，比如将客车、货车分离运行．如果没有通过定量计算，只是定性分析，需要考虑的因素覆盖面广、没有针对性，并不能最大可能的降低列车晚点频率．

3 结 语

本文在已有的基本模糊Petri网建模方法的基础上，通过定义一种用于知识表示的扩展模糊Petri网(EFPN)，分别从人、列车、设备、线路、天气5个方面选出容易造成对列车运行晚点的几个主要因素，分析其因果关系，建立EFPN模型，并根据EFPN模型的推理算法计算各致因因素导致列车晚点的真实度．通过定量分析得到枢纽能力差是导致实例中的列车晚点的最主要因素的结论，证明了通过该模型和算法来分列车致因因素是可行的．

［1］ 郭晓阳. 我国铁路运输发展趋势研究[J]. 合作经济与科技，2012(2)：10–12.

［2］ 彭明鑫. 铁路旅客列车晚点的原因及思考[J]. 江苏交通，1999(12)：19–21.

［3］ 杨彪. 提高高速列车正点率的对策研究[J]. 铁道运输与经济，2012，34(12)：53–57.

［4］ David R，Alla H. Discrete，continuous，and hybrid Petri nets [M]. Berlin：Springer-Verlag，2010.

［5］ Lefebvre D，Delherm C，Leclercq E，et al. Some contribution with Petri nets for the modeling，analysis and control of HDS[J]. Nonlinear Analysis：Hybrid Systems，2007，1(4)：451–465.

［6］ Chen S M，Ke J S，Chang J F. Knowledge representation using fuzzy Petri nets[J]. IEEE Transactions on Knowledge and Data Engineering，1990，2(3)：311–319.

［7］ 王冬冬，达庆利. 基于模糊Petri网的供应链诊断建模分析[J]. 东南大学学报：自然科学版，2006，36(4)：662–666.

［8］ 杨劲松，凌培亮. 一种模糊Petri网的逆向知识推理方法设计实现[J]. 计算机科学，2009，36(12)：158–160.

［9］ 杨其宇，张霞. 模糊Petri网故障诊断技术应用[J]. 兵工自动化，2006，25(4)：73–74.

［10］ 王燕平，马良荔，刘永葆. 基于扩展模糊时间Petri网故障诊断[J]. 计算机工程，2010，36(18)：52–56.

责任编辑：常涛

Modeling and Analyzing Train Running Delays Causation Based on an Extended Fuzzy Petri Net

WANG Shihui，LI Xiaozhong

(College of Computer Science and Information Engineering，Tianjin University of Science & Technology，Tianjin 300222，China)

In view of the serious situation of train running delays，an extended fuzzy Petri net was proposed(extended fuuzy Petri net，EFPN)，and on the basis of some critical factors easily causing delays，a train delay causal analysis model based on EFPN was constructed after simulating and analyzing the causality of the given factors. EFPN reasoning algorithm was used to analyse and calculate the validity of the factors which lead to train delays，and the highest validity of the cause is the most key factor of train delays. Case analysis indicates that EFPN model can reflect the logical relationship among various factors，and it can get the main causes of train running delays through quantitative analysis.

train delays；EFPN；causal analysis；validity

TP399

A

1672-6510(2014)04-0053-05

10.13364/j.issn.1672-6510.2014.04.012

2013–12–05；

2014–02–27

国家自然科学基金资助项目(61070021，11301382)

王诗慧（1989—），女，内蒙古乌兰察布人，硕士研究生；通信作者：李孝忠，教授，lixz@tust.edu.cn.