n阶圈图关联矩阵的特征值
莫贵圈
(贵州师范学院数学与大数据学院,贵州贵阳550018)
0 引言
图论是数学的一个分支,它是以图为研究对象,研究结点和边组成的图形的数学理论和方法。圈图是图论中的一类图形。目前,已有不少学者对圈图进行了研究,例如文献[1]分别讨论了圈外有0个顶点和t个顶点的单圈图关联矩阵的特征值,并证明了特征值完全反映了圈上的顶点个数和圈外的顶点个数;文献[2]研究了包含一个∞—图为其导出子图的一类双圈图匹配多项式的最大根的取值范围,以及达到极值的图;文献[3]研究了两类连通双圈图的最大特征值,得出了随着n的增大,双圈图Sn(3,3)和θn(3,3)的最大特征值也随之增大;文献[4]研究了给定阶数的k圈图的最大Laplace 分离度,并刻画了相应的极图。
图可以用集合来表示,也可以用矩阵来表示。用矩阵表示图便于用代数方法来研究图的性质,也便于用计算机来处理图。常用的图的矩阵表示有: 关联矩阵、邻接矩阵和可达矩阵。图的关联矩阵用来表示各个结点和每条边之间的关系,是描述一个图中结点与边关联性质的矩阵。关联矩阵也是学者们讨论的热点之一,例如文献[5]研究了关联矩阵的一些特殊性质;文献[6]研究了利用邻接矩阵和关联矩阵来判断无向图同构的方法;文献[7]介绍了邻接矩阵与关联矩阵在图论问题中的一些应用,解决了最大匹配、最小顶点覆盖、选址等问题;文献[8]重点研究了n阶无向圈图的关联矩阵的行列式和秩,以及n阶有向圈图的关联矩阵和邻接矩阵的行列式、秩等代数性质。
1 预备知识
定义1[9]137(1) 设G=〈V,E〉为n(n≥3)阶无向简单图,V={v1,v2,…,vn},E={(v1,v2),(v2,v3),…,(vn-1,vn),(vn,v1)},则称G为n阶圈图,记作Cn.
(2) 设D=〈V,E〉为n(n≥2)阶为有向简单图,V={v1,v2,…,vn},E={〈v1,v2〉,〈v2,v3〉,…,〈vn-1,vn〉,〈vn,v1〉},则称D为n阶圈图,也可记作Cn.
定义2[9]144设无向图G=〈V,E〉,V={v1,v2,…,vn},E={e1,e2,…,em},令mij为顶点vi与边ej的关联次数,则称(mij)n×m为G的关联矩阵,记作M(G).
定义3[9]145设G=〈V,E〉为无环的有向图,V={v1,v2,…,vn},令E={e1,e2,…,em},令
则称(mij)n×m为G的关联矩阵,记作M(G).
定义4[9]146设有向图D=〈V,E〉,V={v1,v2,…,vn},|E|=m,令aij(1)为顶点vi邻接到顶点vj的边的条数,称(aij(1))n×n为D的邻接矩阵,记作A(D).

HRCT与常规CT均可见IPF病患的肺部病灶呈弥漫分布,两肺下叶及胸膜下尤甚,其主要征象表现为:(1)胸膜增厚;(2)支气管扩张,呈柱状、囊状性扩张;(3)胸膜下线,其胸膜下10毫米内和胸膜平行、垂直的不均性线形影,尤以背段、外基底段及肺下叶后多见;(4)小叶肺气肿,其表现为小囊腔大量聚集,与蜂窝状相似,多见于下叶;(5)胸膜增厚,小叶间隔性不规则增厚,胸膜下的小叶内出现细网状或细线状影。
2 主要结果及证明

证明:因为Cn是n阶无向圈图,所以Cn的关联矩阵为:
则M(Cn)的特征多项式为:
|λE-M(Cn)|
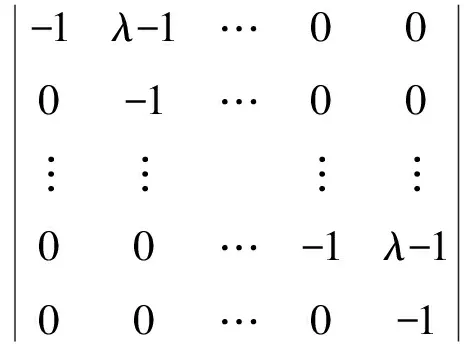
=(λ-1)n+(-1)1+2n
=(λ-1)n-1

定理2 设Cn是n阶有向圈图,则Cn的关联矩阵M(Cn)的特征值分别为:
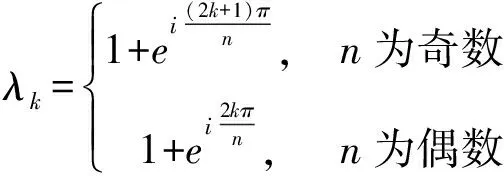
证明:因为Cn是n阶有向圈图,所以Cn的关联矩阵为:
|λE-M(Cn)|

=(λ-1)n+(-1)n+1.




证明:因为Cn是n阶有向圈图,所以Cn的邻接矩阵为:
则A(Cn)的特征多项式为:
|λE-A(Cn)|
=(-1)2n+1+λn
=λn-1

应用上面的定理3,可以证明下面的结论。
推论1 复数域上所有n次单位根的和为0.
证明:设Cn是n阶有向圈图,则Cn的邻接矩阵为:


