分形集上基于延迟矩阵指数的一类时滞微分方程解的表示
邱克娥,熊胜兰,陶 磊,石昌梅,欧阳建新
(1.贵州师范学院数学与大数据学院,贵州贵阳550018;2.贵州师范大学数学科学学院,贵州贵阳550025)
0 引言
时滞微分方程主要用于描述依赖当前和过去历史状态的动力系统。产生时滞的原因很多,如信号的传递需要一定的时间,药物化学反应过程会产生时滞。该方程数学模型比常微分或差分方程更合理地反应了事物的演变规律,使其在物理、信息、生物数学等领域被广泛应用。但由于时滞微分方程的无穷维特点,导致难以恰当地给出精确解,进而使系统的稳定性或可控性等定性分析受限。因此,很多学者都关注于时滞微分系统解的精确表示。2003年,KHUSAINOV 和SHUKLIN[1]首次提出了延迟矩阵指数概念,并利用其重要性质得到了带有可置换矩阵条件下的一阶线性时滞微分方程解的显式表达。2006年,DIBLK和KHUSAINOV[2]将文献[1]的思想发展到离散延迟矩阵指数,得到离散时滞系统的显式解。2018年,MEDVED′和 POSPIL[3]在矩阵不可交换条件下,得到非常系数和可变多时滞微分方程解的表示。目前,很多学者对时滞微分方程展开了其他相关研究[4-5]。
另外,在描述涉及连续不可微函数的物理现象时,分形理论起到了重要作用,受到学者们的关注[6],使分形理论得到不断发展和完善。YANG[7-8]系统地构建了分形空间上的局部分数阶微积分理论,使得许多研究问题被推广到分形集Rα(0<α≤1)上。
受上述研究成果的启发,本文在前人研究的基础上,恰当地构造了分形集Rnα(0<α≤1)上的延迟矩阵指数和Mittag-Leffler型矩阵指数函数,将常微分方程中经典的常数变易法推广到时滞微分方程,最终得到方程
(1)
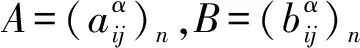
1 预备知识
根据YANG的分形集理论,令Rα(0<α≤1)为分形实线的α型集合。若aα,bα,cα∈Rα,则在Rα中代数运算定义如下[7-8]:
(1)aα+bα∈Rα,aαbα∈Rα,
(2)aα+bα=bα+aα=(a+b)α=(b+a)α,aα-bα=(a-b)α,
(3)aα+(bα+cα)=(a+b)α+cα,
(4)aαbα=bαaα=(ab)α=(ba)α,
(5)aα(bαcα)=(aαbα)cα,
(6)aα(bα+cα)=aαbα+aαcα,
(7)aα+0α=0α+aα=aα,且aα1α=1αaα=aα.
定义1[7-8]设f:R→Rα,x→f(x)是一个不可微函数,如果对任意的ε>0,总存在δ>0(其中ε,δ∈R),使得当|x-x0|<δ时,有|f(x)-f(x0)|<εα,则称不可微函数f(x)在x0处局部分数阶连续。如果f(x)在区间[a,b]上局部分数阶连续,记为f(x)∈Cα[a,b].
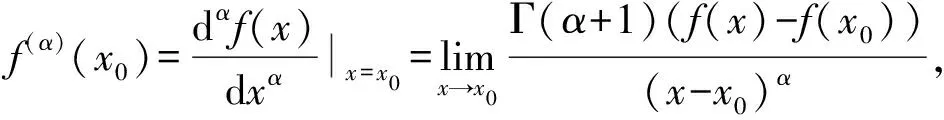
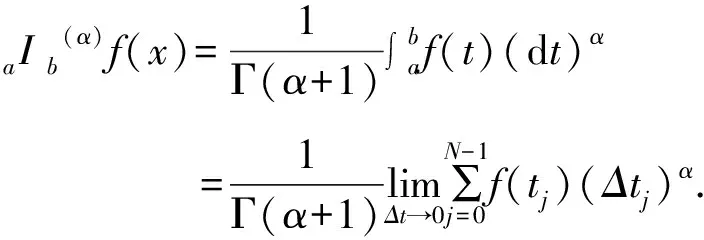
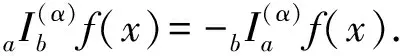
定义4 分形集Rnα(0<α≤1)上,定义延迟矩阵指数具有如下形式:
其中Θ和I分别指零矩阵和单位矩阵。
定义5 分形集Rnα(0<α≤1)上,Mittag-Leffler型矩阵指数函数定义如下:
引理1[7-8](1)设f(x)=g(α)(x)∈Cα[a,b],则aIb(α)f(x)=g(b)-g(a).
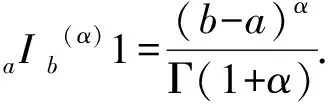
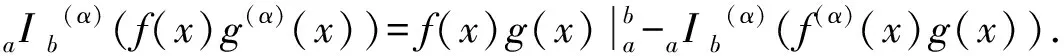
(3)设f(x)∈Cα[a,b],则对任意x∈[a,b]和u∈C1[a,b],有
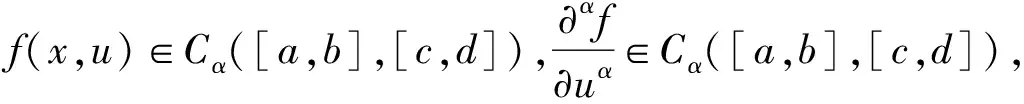
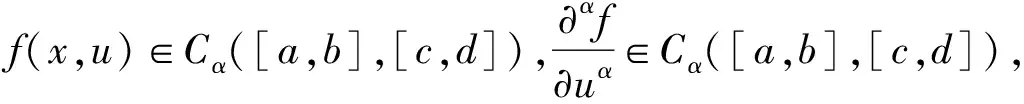
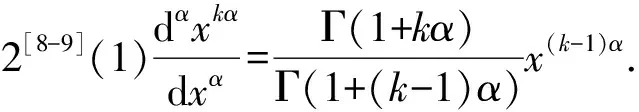
(b(k+1)α-a(k+1)α),k>0.
引理3[7-8]设f(x),g(x)∈Dα[a,b],则对∀λ,γ∈R,有
(1)(λf(x)±γg(x))(α)=λf(α)(x)±γg(α)(x).
(2)(f(x)g(x))(α)=f(α)(x)g(x)+f(x)g(α)(x).
(g(x)≠0).
(4)设g(x)=f(u(x)),且f(α)(u),u′(x)存在,则g(α)(x)=f(α)(u)(u′(x))α.
引理4[7-8]设f(x),g(x)∈Cα[a,b],则对∀λ,γ∈R,有
(1)aIb(α)(λf(x)±γg(x))=λaIb(α)f(x)±γaIb(α)g(x).
(2)aIb(α)f(x)=aIc(α)f(x)±cIb(α)f(x),(a (2) 证明:对于固定的矩阵B及延滞常数τ,利用定义4知引理的证明分为以下三个步骤: (3)对∀x∈[(k-1)τ,kτ],k∈N,应用引理2和引理3,对延迟矩阵指数计算局部分数阶导数得到: 故(2)式成立,引理5得证。 (3) 证明:对于固定的矩阵B及延滞常数τ,对∀x∈[(k-1)τ,kτ],k∈N,由定义4及引理4有 (4) 对(4)式,应用引理1、引理2、引理4,经过简单的计算可得: ③内径、流量、功率推算法。例如:C机井经测量机井内径为225 mm,经询问管理人员,该机井功率为37 kW,每小时出水量为38 m3,井深200 m左右。经推算,机座号确定为200(机座号应小于或等于机井内径);根据流量,可确定机井铭牌流量为40 m3,结合功率37 kW,则该机井型号为200 QJ 40—182/14。 故(3)式成立。 通过定义4,对∀x∈[(k-1)τ,kτ],k∈N,有 又因为(a+b)α=aα+bα,故 综上,引理6成立。 引理7 分形集Rnα(0<α≤1)上,Mittag-Leffler型矩阵指数函数满足(EAxα)(α)=AEAxα. 证明:由定义5、引理2和引理3可得: 本节主要考虑在矩阵A,B可交换条件下,求方程(1)的显式解。首先利用第1部分的预备知识,得到方程(1)的基解矩阵。其次,考虑方程(1)所对应的齐次方程的解和非齐次初值条件为零的解。最后得到方程(1)的显式解。 (5) 定理证毕. (6) 的解具有如下形式 证明:由定理1及解的结构知,方程(6)的解具有如下形式 (7) 由A,B的可交换性,有 (8) v(s)(ds)α. (9) 对 (9)式关于x求α阶局部分数阶导数,并利用引理1、引理3、引理7有 从而Aφ(x)-φ(α)(x)=-E-Aταv(x),也即是v(x)=EAτα(φ(α)(x)-Aφ(x)).将v(x)代入(8)式,得到 (10) 的解具有如下形式 (11), 其中F(s)是定义在[0,x]上的未知向量函数。对(11)式求α阶局部分数阶导数,利用引理1和引理4有 (12) 将(11)和(12)式代入方程(10),有 因为B1=E-AταB,上式可变形为 (13) 定理4 方程(1)的解具有如下形式: 证明:结合定理2和定理3知道,定理4成立。 文章主要根据YANG[7-8]建立的局部分数阶积分理论,在分形集Rnα(0<α≤1)上构造延迟矩阵指数和Mittag-Leffler型矩阵指数函数,将常微分方程中经典的常数变易法推广到时滞微分方程,最终得到一类带时滞微分方程解的显式表达,进而有利于对一些系统的稳定性或可控性等定性分析进行研究。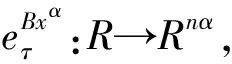
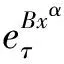
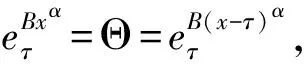
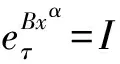
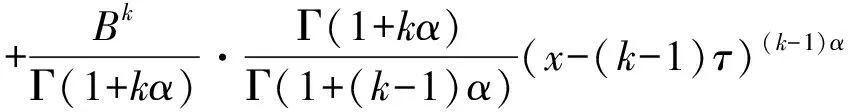
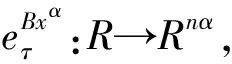
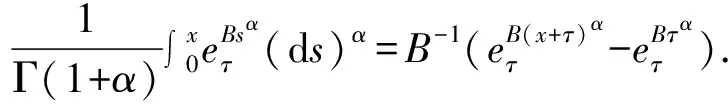
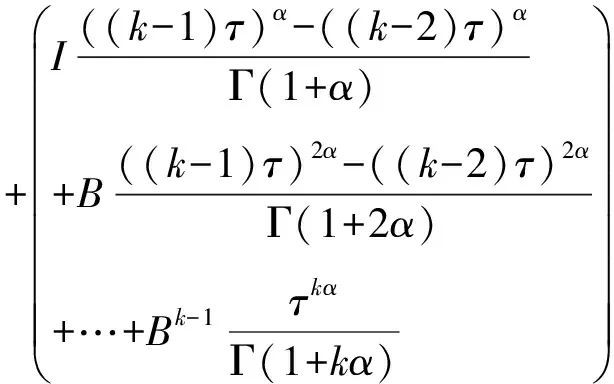
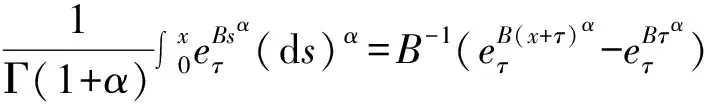
2 主要结果及证明
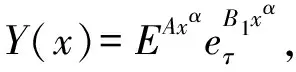
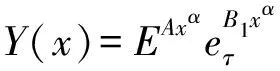
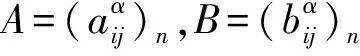
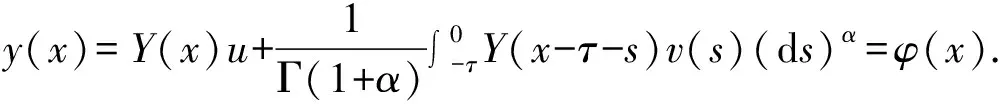
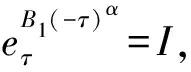
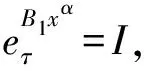
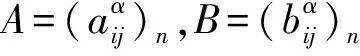

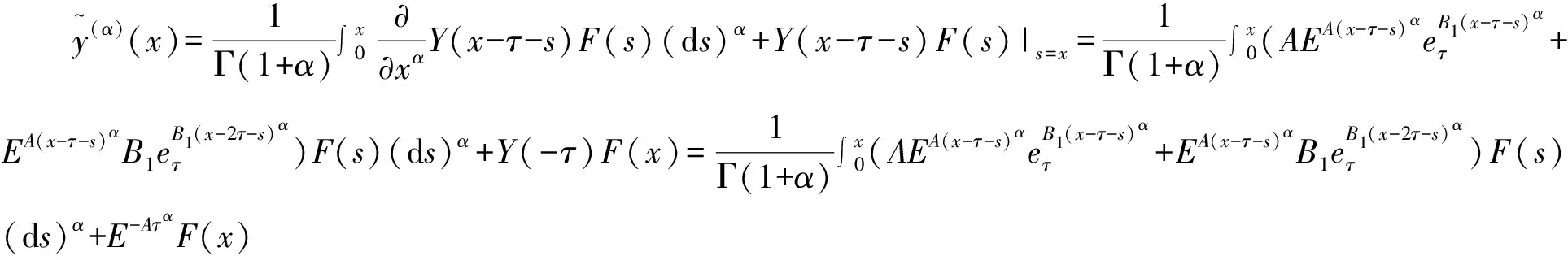
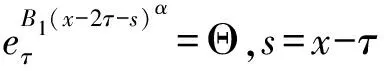
3 结束语

