数学竞赛不等式一题多解的数学教育价值
张传军,张东方,侯先融
(1. 贵州师范学院教育科学研究所,贵州贵阳550001;2. 广州市滨江五中学校,广东广州510006;3. 黔南民族师范学院数学与统计学院,贵州都匀558000)
0 引言
不等式是高中数学中的重要内容之一,是数学基础理论的重要组成部分,是衡量事物间数量关系的重要数学模型。不等式也是竞赛数学中不可或缺的一部分,在竞赛中占有一定的比例。数学竞赛考试内容主要分为四个部分:平面几何、代数、初等数论和组合问题,其中代数部分是竞赛的重点,考试占比最大,而不等式又是代数部分的重点,每年都有几道不等式的相关试题。
近年来,不等式在竞赛试题中是常客,每年都会有不等式的相关试题。下面列举2014至2019年连续六年的部分试题。2014年全国高中数学联赛加试卷第1题,2015年全国高中数学联赛一试第9题和加试第1题,2016年全国高中数学联赛一试第1、9题和加试题第1题,2017年全国高中数学联赛一试A卷第2、9、10题,2018年全国高中数学联赛一试第10题和加试题第一题,2019年全国高中数学联赛一试第10题和加试题第一题均涉及到不等式的相关知识。并且,近些年的全国高中数学联赛二试的第1题大多是不等式题目。
目前,关于竞赛数学以及竞赛不等式的内容有不少研究成果。周莹的《高中数学竞赛不等式应用研究》[1]主要研究总结了不等式在多变量函数求极值问题以及含参不等式恒成立问题两个方面的应用。李玉的《舒尔不等式在高中数学竞赛中的研究》[2]主要研究了舒尔不等式及其一些变式在高中数学竞赛中的应用。白益雪的《浅谈数学竞赛对于学生能力的培养》[3]探究了数学竞赛对学生创造性思维培养的影响。邵国军的《高中竞赛数学思想方法及其教育价值研宄》[4]中分析了柯西不等式在一道题目中的作用。李小娟的《中学数学竞赛中的柯西不等式问题探究》[5]中主要分析了数学竞赛中涉及到柯西不等式的题目以及编题。朱鑫磊的《浅析高中数学竞赛的解题思维》[6]先就高中数学竞赛特点进行分析,并采用相关例再行佐证,再简要指出高中数学竞赛的解题思维策略。本文在这些研究的基础上,通过一道数学竞赛不等式题目的一题多解,深刻阐释了不等式对数学思维培养的影响及其蕴含的数学教育价值。
1 解不等式的常用方法
常用的不等式的证明方法有比较法、综合法、分析法、数学归纳法、反证法、放缩法、函数法等。本文通过展示例题的“一题多解”,主要介绍了综合法、分析法、数学归纳法和放缩法在不等式问题中的具体运用,从而说明数学竞赛中不等式问题所具有的数学教育价值。
1.1 综合法
综合法是从己知条件出发,依据题设所给的不等式的特征和已熟知的不等式的性质来逐步推导出不等式的证明方法。
1.2 分析法
分析法是从所需求的结论出发,推导使不等式能够成立的充分条件或者是充要条件,直到推导出题设的条件或者己知的结论为止的证明方法。若题设满足推导的条件则判定原来的不等式成立。
1.3 数学归纳法
数学归纳法是证明不等式的一种常用且有效的方法。具体步骤是先设一个关于正整数n的命题,证明n=1时该命题成立,再假设当n取第k个值时该命题成立,然后利用假设条件和已知条件推导出n取第k+1个值时该命题也同样成立,那么最后可以得出该命题成立。
1.4 放缩法
放缩法是在证明不等式成立的过程中将某些部分放大或者缩小成容易判断的式子,利用不等式的传递性再证明原不等式成立。放缩法是一种非常重要的证明方法,在竞赛和考试中经常使用。
2 例题内容及剖析
2.1 例题内容
已知:设正实数a1,a2,…,a100,满足a101-i≤ai(i=1,2,…,50),
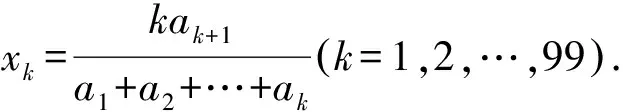
证明:x1x22…x9999≤1.
2.2 例题剖析
数学竞赛的试题是充满创造力的数学问题,其构思别致、结论简洁、方法新颖,具有独特的数学魅力[3]。本题选自2019年全国高中生数学联赛加试第1题,属于代数部分中不等式的知识。题目综合性、创新性较强,重在考查学生的基础知识体系以及创造性思维。解答该题需要学生有扎实的基础以及良好的数学思维,能够活学活用,利用已有的数学知识和解题经验完成该证明。
3 例题的五个解法分析
3.1 解法一(参考答案)
证明:注意到a1,a2,…,a100>0.对k=1,2,…,99,由平均值不等式知
从而有
①
记①的右端为T,则对任意的i=1,2,…,100,ai在T的分子中的次数为i-1,在T的分母中的次数为100-i.从而
又0 x1x22…x9999≤T≤1. 解法分析:这种解法使用了综合法和放缩法,其核心在于运用均值不等式的性质对代数式进行放缩,要诀在于代数式的合理变形,解答过程漂亮、简练,巧妙地将式子变形并利用已知条件证明之。 证明:由于ai(i=1,2,…,100)∈R+, 故 ≥1, 故x1x22…x9999≤1,当且仅当a1=a2=…=a100=1时等号成立。 解法分析:同时运用了综合法、分析法和放缩法。由已知条件出发,利用高中生所熟知的均值不等式对式子进行放缩,再将欲证明的式子进行合理变形重组,利用已知条件证之。 证明:预证x1x22…x9999≤1 对不等式两边同时取对数得ln(x1x22…x9999)≤0,即lnx1+2lnx2+…+99lnx99≤0. 又klnxk=klnk+klnak+1-kln(a1+a2+…+ak) lnx1≤lna2-lna1, 2lnx2≤2lna3-lna1-lna2, 3lnx3≤3lna4-lna1-lna2-lna3, ⋮ 99lnx99≤99lna100-lna1-lna2-…-lna99, =99(lna100-lna1)+97(lna99-lna2)+…+(lna50-lna51). 又a1,a2,…,a100满足a101-i≤ai(i=1,2,…,50). 故lna100-lna1≤0, lna99-lna2≤0, lna50-lna51≤0, 即原式成立。 解法分析:主要运用分析法和放缩法,巧妙地运用转化思维。首先把复杂的高次代数式转化为简单的对数式,其次利用均值不等式对式子进行放缩和变形,最后利用已知条件证明了该命题。 ∵对i∈{1,2,…,99},有 ai100-ia101-ii-1=aii-1ai101-2ia101-ii-1 ≥aii-1a101-i101-2ia101-ii-1 =aii-1a101-i100-i ∴a199≥a10099,a298a99≥a2a9998…a5050a5149≥a5049a5150 即x1x22…x9999≤1. 解法分析:主要运用分析法和放缩法,先将原命题等价变形,其次利用均值不等式将其放缩,再次利用已知条件对式子进行变形与二次放缩,最终完成等价命题的证明。 证明:设sn=a1+a2+…+an ∵ai≥a101-i 不妨设:a1≥a2≥…≥a100 ⋮ ∴x1x22…x9999 要证①≤1,即证 当n=1时,1·a2≤a1成立。 假设当n=k时,k·ak+1≤sk成立。 即k·ak+1≤a1+a2+…+ak. 当n=k+1时, (k+1)·ak+2=k·ak+2+ak+2 ≤k·ak+1+ak+1≤sk+ak+1=sk+1. ∴n·an+1≤sn成立。 即原式成立。 解法分析:主要运用数学归纳法,并未借助均值不等式,而是另辟蹊径将与原命题等价的分式不等式转化为整式不等式,再利用数学归纳法证明之。 通过本题的解答我们可以得出:同一个问题,用不同的思维方法,都可以得以解决,并且同一种思维方法,也可以有不同的呈现方式。例如解法一、解法二、解法三、解法四的核心都是均值不等式,虽然每一种解法的变形、转化都是不一样的,但结果殊途同归。同时对于解法五,从一个新的角度出发,用数学归纳法完成了对该命题的证明。纵观本题的几种解法,不难看出,在应对竞赛试题时,需要学生具有较强的解题能力、创新能力以及良好的数学思维,要能够在做题时正确地捕捉题目关键信息并对所获得的信息进行加工处理,构建题干的信息链,理顺各部分题干的关系,得出解题思路并完成对题目的解答。 中学数学的六大核心素养为:数学运算、逻辑推理、直观想象、数学建模、数据分析、数学抽象。不等式由于其本身的综合性可以和许多知识进行串接,故可以涵盖核心素养的各个方面。但由于本研究选题的特殊性,主要涉及了数学抽象、数学运算、逻辑推理这三方面的素养。 4.1.1 不等式问题促进学生数学运算素养的提升 在数学解题中,几乎离不开数学运算。在例题解答中,每一种解法里都需要进行数学运算,并且需要学生掌握一定的解题技巧,需要对式子进行变形和放缩等,特别是解法一中对表达式T的等价变换更是需要学生具有很强的运算能力和解题技巧,才能完成如此简洁漂亮的变形。 4.1.2 不等式问题促进学生数学抽象素养的提升 从解题过程不难看出,解题时需要学生能够从题目中找出解题的关键信息,明确数学概念等,这就要求学生具有一定的抽象的数学素养。从培养学生核心素养的层面来说,通过此类题目能够培养学生数学抽象方面的素养,学习从事物的具体背景中抽象出一般规律和结构,并且能准确地用数学符号和数学语言表述自己的解题过程。让学生能更好地理解数学的相关概念、命题、方法,能通过抽象、概括去认识和理解把握数学的本质。 4.1.3 不等式问题促进学生逻辑推理素养的提升 逻辑推理是数学严谨性的基本保证,是人们在数学活动中进行交流的基本思维品质。学生在解题过程中,尤其要注意解题步骤前后的逻辑性和连贯性,不能出现逻辑性的错误,对于所使用的定理的条件以及结论必须是清晰明白的。因为在解题过程中会出现多个定理或者知识点间的串接,所以要尤为注意整体解题的逻辑性。在逻辑推理核心素养的形成过程中,学生能掌握推理的基本形式,表述论证的过程;能理解数学知识之间的联系,建构知识框架;形成有论据、有条理、合乎逻辑的思维品质,增强数学交流能力。在教学中,教师要能够站在一个新的高度,立足于多种方法,让学生经历从多角度思考问题、多渠道解决问题,一直到提炼核心本质的过程,这是发展学生数学逻辑推理素养的重要途径[7]。 数学竞赛所呈现的题型具有较强创新性和综合性,大多都有多种不同的解法,从而促进学生思维发散,灵活运用已有的数学知识和经验,对竞赛题目进行求解,培养学生的数学创造力与洞察力。因此数学竞赛解法多样化是培养学生数学思维能力的关键因素之一[8]。进行有效的一题多解训练可以让学生感悟知识的内涵,方法的通用性与局限性,对提高学生的思维能力有极大的帮助[9]。教师在日常融入了数学竞赛内容的教学活动中,通过多样化解题提升了学生对数学知识的掌握,同时还能够通过运算促进其数学思维发展,并形成一丝不苟、严谨求实的科学精神。 本文通过对高中数学竞赛中一道不等式题的一题多解探究,分析了综合法、分析法、数学归纳法、放缩法等解不等式常用方法在实际解题过程中的综合运用。从整体来说,数学竞赛题目的考察更趋于综合性,灵活性也更加突出,需要学生有纵观全局的观察力,能深入地分析问题,找到各知识点之间的联系,以锲而不舍的精神去探究,发挥自身的创造力,进而求解数学问题[10]。 在教学中应用数学竞赛一方面可帮助学生巩固数学基础知识,进一步丰富学生自身的知识储备促进学生核心素养的培养。另一方面可加深学生对数学知识本质和数学思想方法的认识和理解,提升学生的数学思维,让学生得到更加全面的发展。3.2 解法二
3.3 解法三
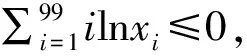
3.4 解法四
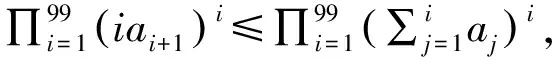
3.5 解法五
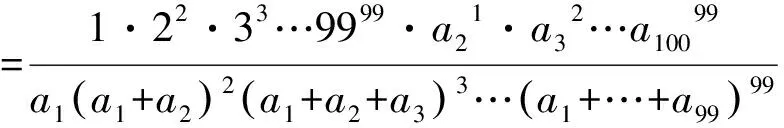
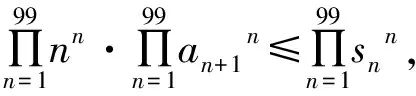
3.6 例题小结
4 不等式问题促进学生核心素养的发展和数学思维的培养
4.1 不等式问题促进学生核心素养的发展
4.2 不等式问题促进学生其他数学思维能力提高
5 结语

