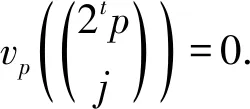一些特殊第二类Stirling数的p-adic赋值
吉庆兵, 卢 健
(1. 西北工业大学网络空间安全学院, 西安 710072; 2. 中国电子科技集团公司第三十研究所, 成都 610041)
1 引 言
设N是非负整数集合. 定义在N上的第二类Stirling数表示将n个元素划分为恰好k个非空集合的个数, 记为S(n,k),其中k和n为非负整数. 熟知,S(n,k)有如下的表达式
(1)

注意到S(n,k)有如下的显性表达式
同时,S(n,k)有生成函数
以及如下的关系式
成立,其中(x)k为递降阶乘,对k≥1,(x)k定义为x(x-1)(x-2)…(x-k+1),(x)0=1.此外,令S(0,0)=1.当n≥0时,S(n,0)=0.当n≥k≥1 时,S(n,k)满足递推关系
S(n,k)=kS(n-1,k)+S(n-1,k-1).
正整数序列的整除性是数论等领域中十分有趣并且富有挑战性的课题. 其中,第二类Stirling数S(n,k)的整除性问题在数论、组合论、代数拓扑等领域都得到了广泛研究. 对任意给定的素数p和正整数n, 存在惟一的整数m, 使得n=apm, 其中(a,p)=1.我们称m为n的p-adic赋值, 并记vp(n)=m.p-adic赋值是表示整除性常用的一种方式. 许多作者研究了第二类Stirling数的整除性, 包括Davis等[1],Hong等[2]和Zhao等[3-5]. 其中,Bendersky和Davis[6], Davis等[7,8,1]对一类S(n,k)的p-adic赋值进行了深入研究, 给出了min{vp(k!S(n,k)),1≤k≤n}数值问题的一些结果,并将其应用于代数拓扑的某些问题. Davis[9]和 Clark[10]利用Hesel引理建立了当k≤7且n<2100时v2(k!S(n,k))的计算公式. 同时,Clark[10]提出猜想: 设p为素数且n≥k, 则vp(k!S(n,k)) 最近, Zhao和Qiu[5]研究了当p为奇素数时vp(S(n,k))的一些结果, 特别地,vp(S(p,2))≥1; 当n≥2时,vp(S(pn,2p))≥n; 当n≥2,p≥5时,vp(S(pn,4p))≥n-2. 在本文中, 我们利用二项式系数的p-adic赋值得到了更一般的结果: 定理1.1设p为奇素数,t和n为正整数且n≥2, 2≤2t 设k和n为非负整数.令S(0,0)=1.当n>0时,S(n,0)=0.当k>0时,S(0,k)=0. 显然,当n 根据式(1)易得S(n,1)=1.当n≥2时,有S(n,2)=2n-1-1. 记sp(n)为n的p-adic表示(将n表示为以p为基底)的指标和. 关于二项式系数的p-adic赋值有如下结论. 引理2.1[15]设p为素数,k和n为非负整数,则有 (2) 且对所有0≤k≤n有 (3) 引理2.2[5]设p为奇素数,i,k和n为正整数且满足1≤k≤p-1, 1≤i≤kp-1, (i,p)=1, 则有vp((kp-1)pn+ipn)=n+1. 引理2.3设p为奇素数,j和t为正整数且满足2≤2t 证明 首先由式(3)可得 (4) 情形2:(j,p)=1. 由1≤j≤2tp-1, 2≤2t 2tp-j=2tp-a-bp= (p-a)+(2t-1-b)p, 其中1≤p-a≤p-1 , 0≤(2t-1-b)≤(2t-1) sp(j)=a+b, sp(2tp-j)=(p-a)+(2t-1-b)= 2t+p-a-b-1, sp(2tp)=2t. 则由式(4)计算可得 引理得证. 定理1.1的证明 首先,根据式(2)可得 其次,根据式(1)有 vp(A0)=vp((2tp)pn)-vp((2tp)!)=pn-2t (5) vp((2tp)!)≥pn-2t (6) 对正整数j, 1≤j≤2tp-1, 若(j,p)=1, 2≤2t 由引理2.2可得 vp((2tp-j)pn+jpn)=n+1. vp((2tp-j)pn+jpn)-vp((2tp)!)= n+2-2t (7) 故 因此 vp(S(pn,2tp))≥ 由式(5)可得vp(A0)=pn-2t.由式(6)可得 由式(7)可得 从而当n≥2时有pn>n+2.因此vp(S(pn,2tp))≥n+2-2t.定理得证. 设t=1, 则由定理1.1有 推论3.1设p为奇素数,n为正整数且n≥2, 则有vp(S(pn,2p))≥n. 设t=2, 由p≥2t≥2, 利用定理1.1可得vp(S(pn,4p))≥n+2-22=n-2,即 推论3.2设p为奇素数,n为正整数且n≥2,p≥5. 则vp(S(pn,4p))≥n-2. 注推论3.1即为文献[5]中定理1.2,推论3.2即为文献[5]中定理1.3.2 预备知识

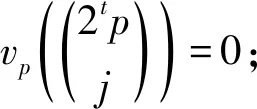


3 主要结果的证明