基于平衡附加力原理的微动放大机构设计与实验

杨满芝 李林岳 张传伟 魏凯洋 党 蒙 景 钢

(西安科技大学机械工程学院， 西安 710054)

0 引言

随着现代科学技术的不断发展，精密、超精密加工技术成为机械加工非常重要的方向，对精密运动进行研究具有重要意义[1-5]。在精密运动中，微动机构既能作为微动系统的执行单元输出精密位移，又能作为宏微驱动系统补偿机构实现大型高精度运动[6-9]。目前微动系统大多使用压电陶瓷致动器(Piezoelectric ceramics，PZT)、超磁致伸缩器(Giant magnetostrictive actuator, GMT)等驱动器直接进行驱动，但这些微驱动器的输出位移较小，难以实现较大的微位移运动，从而导致宏微驱动补偿范围较小。为了突破微动机构运动范围的限制，需要对微动放大机构设计及性能进行研究。

为了实现微动机构的放大功能，许多学者对微动放大机构进行了研究。李佳杰等[10]设计了一种利用杠杆原理进行放大的二级差动微位移放大机构，采用应用矩阵表示法对其进行运动静力学分析与优化。SU等[11]设计了一种用于微机电系统的机械放大器，介绍了单级杠杆和多级杠杆在内的设计和综合理论，可根据需求来给出最佳杠杆级数。KEE-BONG等[12]提出了一种新颖的压电驱动柔性平台，该平台引入了两个平行布置的机械放大机构，其输出位移及输出力均得到增大。LING等[13]提出了一种菱形和桥型柔顺机构位移放大率的增强理论模型，并完成了模型建立和有限元分析，得出将桥式弯曲简化为菱形结构进行力学建模位移放大率误差会增大。BOLZMACHER等[14]设计了一种新型微机械放大单元，用于将压电微驱动器的行程增加到高频，以便于在相对较高的工作频率下表现出相对较大的冲程。NICOLAE等[15]基于应变能和Castigliano位移定理解析出封闭形式的方程，制定了一种用于计算具有单轴弯曲铰链的平面柔顺机构的位移和刚度的解析方法。KIM等[16]设计了一种双平行四边形的放大机构，可利用倾斜结构来实现位移放大。

微动机构在运动方向上运动精度要求较高，且微致动器在运动方向一般可承受较大应力，而非运动方向一般较为脆弱[17-25]，如果在工作状态中产生附加位移及附加力，非运动方向附加位移会导致运动不精密，非运动附加力则会对微致动器安全造成严重影响，而以上研究未考虑附加位移及力对微动机构影响。本文设计一种无附加力及附加位移的精密微动放大机构，并对机构强度、动态、运动学进行分析。

1 精密微动放大机构设计

1.1 平衡附加力原理

微动机构的放大功能一般采用如图1所示的杠杆原理工作，右端点q与底座连接，为固定端；s处为位移输入端；t处为位移输出端。在压电陶瓷的输入位移Δu的作用下，输入端沿y方向运动，此时端点q固定，输入位移被放大，在输出端沿y方向运动，将输入位移Δu放大为输出位移Δv。

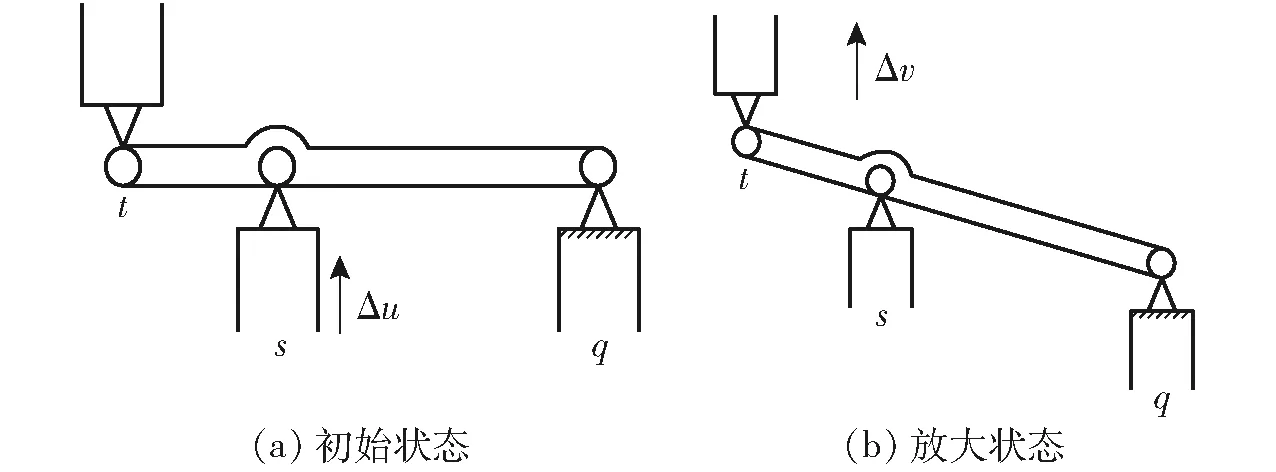
图1 杠杆原理示意图Fig.1 Schematics of lever principle

微动机构的平衡附加力原理如图2所示，将微驱动器在矩形槽E内连接固定，机构对称设计有8个柔性铰链组件(柔性铰链1～16)。当驱动器产生驱动位移时，柔性铰链会发生形变，除产生主运动方向的力外还会产生非运动方向的力，此时对称分布的8个柔性铰链组件由于形变产生的非运动方向的力大小相等、方向相反，可以互相平衡，实现了柔性铰链的附加力及附加位移平衡。平衡附加力原理避免了微动机构产生非运动方向的位移，同时保护了驱动器免受水平方向力的破坏，确保了微动系统的精密性和安全性。

图2 柔性铰链平衡附加力原理示意图Fig.2 Schematic of principle of additional force balance of flexible hinge

1.2 精密微动放大机构设计

根据杠杆原理结合平衡附加力原理，本文设计了一种可将运动输入精密放大的微动机构，设计放大比1∶1.5，结构示意图如图3所示。微动放大机构的外形尺寸为150 mm×157 mm×50 mm。机构包含24个相同的直圆型柔性铰链，每个柔性铰链的半径长度和最小距离分别为3 mm和1 mm(图3的局部放大图)。将机构b部分固定在工作台上，在微驱动器的驱动作用下输入机构a部分获得y轴正向输入位移Δu，根据杠杆原理微动放大机构对输入位移进行y轴精密放大，从输出机构c部分获得输出位移Δv。在机构工作过程中，两侧对称分布的柔性铰链13～24根据平衡附加力原理，非运动方向上的力和位移会进行抵消，使得机构在工作时无附加位移及附加力产生，从而保证机构良好的精密性和安全性。

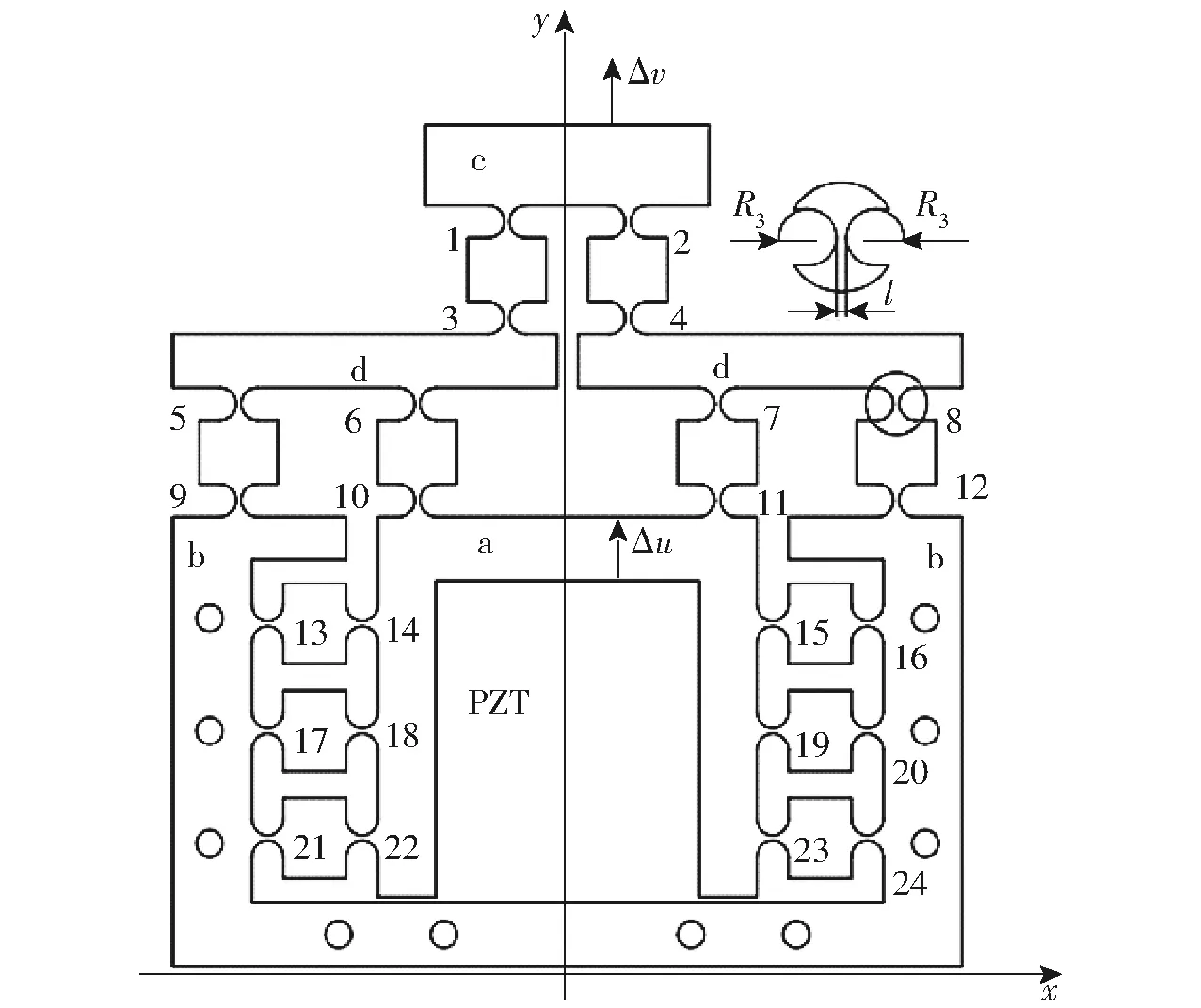
图3 微动放大机构结构示意图Fig.3 Schematic of structure of micro-drive amplifying mechanism

由于柔性铰链是通过自身薄弱部位材料产生的可逆弹性形变来传递运动，所以对材料的选取有较为严格的要求。选用60Si2Mn、65Mn、QBe2作为微动机构材料，其参数如表1所示。

表1 3种柔性铰链材料参数Tab.1 Three material parameters of flexible hinge

1.3 放大比计算

设计微动机构时，可对机构结构进行调整以便获得需要的放大比。以放大比1∶1.5为例，其他场景可根据调整机构结构以获得所需要的放大比。微动机构两侧呈对称分布，在分析时只需对微动放大机构的单侧进行分析。

在微动机构运动过程中，各柔性铰链会产生变形从而使得其回转中心产生偏移，设柔性铰链i(i=1，2，…，24)受到的轴向力为Fi，力矩为Mi，铰链产生的轴向变形量为Δi，转动角为αi，则有

Fi=KFΔi

(1)

Mi=KMαi

(2)

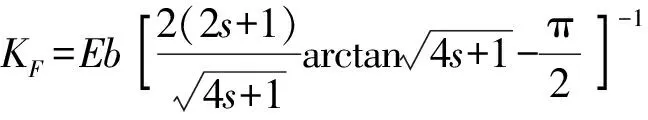
(3)

(4)

式中KF——轴向拉压刚度

KM——转角刚度

E——弹性模量

s——铰链半径与最小厚度之比

在杠杆放大机构中，柔性铰链转角α2和杆件转角θ1之间存在关系

α2=θ1

(5)

微动放大机构受力分析如图4所示。由1.1节微动放大机构工作原理可知，微动放大机构理论放大倍数为

(6)

式中A——微动机构放大比

Y6——柔性铰链6位移

Y3——柔性铰链3位移

l1——杠杆机构的输入端到固定端长度

l2——杠杆机构输出端到固定端长度

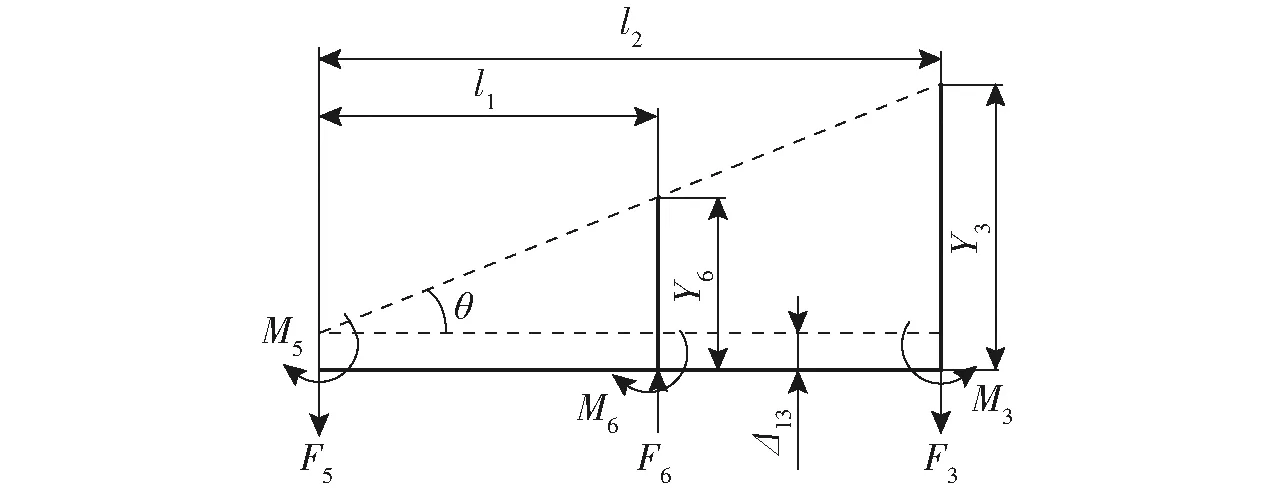
图4 放大比几何计算模型Fig.4 Amplification ratio geometric calculation model

将所设计的微动放大机构的参数代入式(6)计算可得微动放大机构放大比A为1.5。

2 强度

图5 微动放大机构网格划分图Fig.5 Grid division diagram of micro-drive magnifying mechanism

利用有限元软件对微动放大机构模型进行网格划分，如图5所示，模型共划分为366 048个单元，544 272个节点。将微动放大机构上边缘10个螺栓孔圆柱面固定，对机构中驱动器的位置处施加Y轴正向位移15 μm，分析得到微动放大机构应力如图6所示，由图6可知最大模拟应力为41.928 MPa。

图6 微动放大机构应力云图Fig.6 Stress cloud diagram of micro-drive magnifying mechanism

材料许用应力计算式为

(7)

式中 [σ]——材料许用应力

σs——材料屈服极限

λ——安全系数，取1.5

根据式(7)可求得材料的许用应力[σ]为784 MPa，而微动放大机构的最大模拟应力仅为41.928 MPa，远小于材料的许用应力。因此，微动放大机构具有较好的强度性能，且能够满足设计要求。

3 动态性能

3.1 有限元分析

采用有限元法的动力学模块对微动放大机构进行自由模态分析，其前6阶固有频率为529.8、579.11、805.32、964.11、1 198.9、1 304.2 Hz。

3.2 动态性能实验

实验采用德国M+P动态测试控制分析系统、数据采集前端、高精度力锤、橡皮绳、微动放大机构及计算机等实验仪器与设备，进行微动放大机构自由动态实验，实验装置如图7所示。将微动机构用橡皮绳悬挂，数据采集前端固定在机构上，另一端与M+P动态测试控制分析系统相连接，使用高精度力锤敲击自由悬挂的微动机构可以测得其固有频率，微动机构前6阶固有频率实验结果如图8所示。

图7 微动放大机构动态性能实验装置Fig.7 Experimental device of dynamic performance of micro-drive amplifying mechanism1.微动放大机构 2.数据采集仪前端 3.高精度力锤 4.M+P动态测试控制分析系统 5.计算机

图8 微动放大机构前6阶固有频率实验结果Fig.8 Experimental results of the first six order natural frequencies of micro-drive amplification mechanism

通过有限元及实验分析，微动放大机构的前6阶固有频率结果对比如表 2 所示。由表 2可知，有限元及实验分析结果较为一致，其最大相对误差为9.41%，分析结果准确可信。且其最低固有频率为530 Hz左右，而本文选用P235.1s 型压电陶瓷致动器最大驱动频率为300 Hz，因此微动机构在运动过程中不会发生共振现象。因此，微动放大机构动态性能优良，且运动过程中不会发生低频共振现象，符合设计要求。

表2 机构固有频率有限元与实验分析对比Tab.2 Comparison between finite element method and experimental analysis of mechanism’s natural frequency

4 运动学分析

4.1 有限元分析

为了方便研究，对微动放大机构在输入位移0～7 μm范围内的运动性能进行测试，利用印记方法对微动机构施加输入位移0.50 μm，如图9所示，采用probe(探针功能)计算机构输出位移。

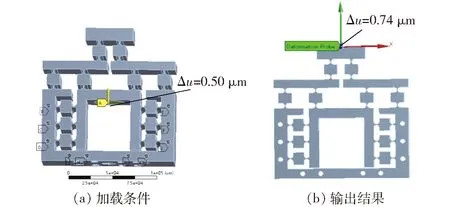
图9 微动放大机构的有限元分析Fig.9 Finite element analysis of micro-drive amplifying mechanism

4.2 运动学实验

实验采用德国PI公司P235.1s型压电陶瓷致动器(其参数见表3)、电感式传感器(1号传感器为旁式传感器，其分辨率为0.03 μm；2号传感器为直式传感器，其分辨率为0.05 μm)、微动放大机构、实验底座、MDG-8型数据采集仪等实验仪器与设备，微动放大机构运动实验如图10所示。实验利用1号传感器(旁式传感器)测量微动机构的输入位移，利用2号传感器(直式传感器)测量微动机构的输出位移，利用压电陶瓷致动器输入不同位移可以获得不同的输出值，实验结果如表4所示。

表3 P235.1s型压电陶瓷致动器主要技术参数Tab.3 Main technical parameters of P235.1s piezoelectric ceramic actuator

图10 微动放大机构实验实物Fig.10 Experimental object of micro-drive amplifying system1.1号传感器 2.PZT 3.2号传感器 4.微动放大机构 5.实验底座

表4 微动放大机构运动学分析3种方法实验结果Tab.4 Comparison of three methods for kinematic analysis of micro-drive amplification mechanism μm

4.3 对比分析

通过式(6)可计算出各个输入位移对应输出的理论分析值，理论分析、有限元分析和实验结果对比如表4所示，对三者分析进行结果拟合如图11所示。

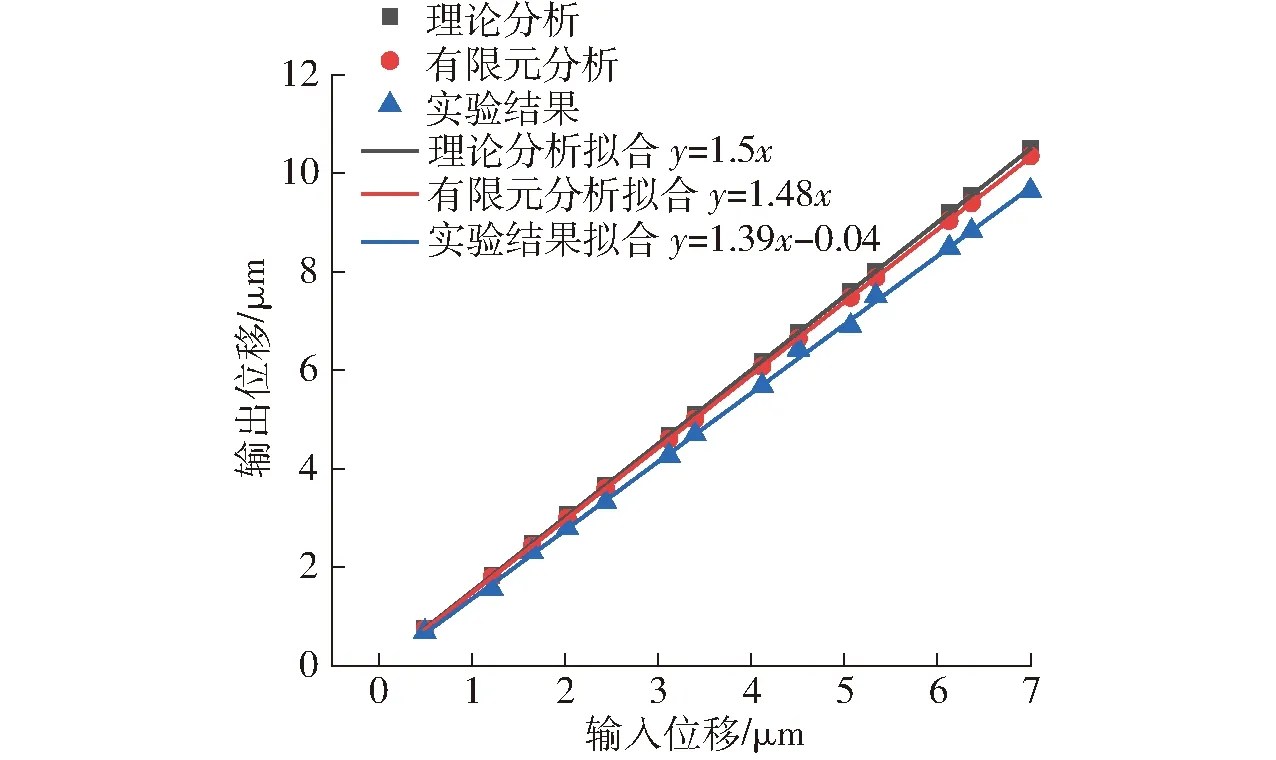
图11 微动放大机构运动学分析Fig.11 Kinematics analysis of micro-drive amplifying mechanism

对理论分析进行拟合，得到线性方程式为

Δv=1.5Δu(R=1)

(8)

对有限元分析进行拟合，得到线性方程式为

Δv=1.48Δu(R=1)

(9)

对实验结果进行拟合，得到线性方程式为

Δv=1.39Δu-0.04 (R=0.998)

(10)

结果表明微动系统的输入位移与输出位移具有运动精度及线性度较高的优点。利用拟合的线性方程(8)～(10)斜率的计算理论分析值与实验值的相对误差为9.4%(二者最大绝对误差为0.85 μm)，有限元分析值与实验值相对误差为7.8%(二者最大绝对误差为0.57 μm)。同时，运动线性拟合相关系数不小于0.998。

为了方便工程应用，根据式(8)～(10)可将微动放大机构的运动输入与输出关系拟合为

Δv=1.456Δu

(11)

误差产生的原因包括机构加工误差、有限元模型导入误差、实验室检测环境误差等，可通过提高加工精度、细化有限元网格、降低实验室振动、噪声等外界干扰等方法降低误差。运动学实验过程中压电陶瓷致动器安全运行，也可证明本文设计的微动机构无附加力存在。

5 结论

(1)设计的一种精密放大机构，系统的放大比可根据需求调节，可将直线位移按照需要放大，以满足不同的大行程高精度应用场合。

(2)设计的微动放大机构根据平衡附加力原理，在工作时不会产生非运动方向力及位移，能够有效保证其运动的安全性及精密性。

(3)采用有限元法完成系统强度分析、有限元法及实验完成动态性能分析，分析结果表明系统强度性能满足设计及使用需求，且系统动态性能良好(一阶固有频率为580 Hz、固有频率分析有限元及实验最大相对误差为9.41%)、运动过程中不会发生共振。

(4)通过理论分析、有限元及实验完成机构运动学分析，结果表明系统运动精度及性能线性度高，并给出了其运动性能拟合方程。运动学分析中理论分析值与实验值相对误差为9.4%，最大绝对误差为0.85 μm；有限元分析值与实验值相对误差为7.8%，最大绝对误差为0.57 μm；机构运动线性方程相关系数不小于0.998。