指向统计意义的百分数教学——《百分数的意义》新课标解读与教学建议

○朱宇

《百分数的意义》是人教版小学数学六年级上册第六单元“百分数（一）”的起始内容。教材通过百分数相关素材的呈现，激活学生生活经验，引导学生理解百分数是两个量之间的倍比关系，会正确地读、写百分数，并运用百分数描述生活中的一些数学现象，突出百分数在生活中的广泛应用。

一、课标变化点

《义务教育数学课程标准（2011年版）》中，百分数属于“数与代数”领域，在内容标准中这样描述：理解百分数的意义，会进行小数、分数和百分数的转化，能解决小数、分数和百分数的简单实际问题。

《义务教育数学课程标准（2022年版）》（以下简称《课标（2022年版）》）将百分数从“数与代数”领域调整到“统计与概率”领域，在内容要求中作了详细描述：结合具体情境，探索百分数的意义，能解决与百分数有关的简单实际问题，感受百分数的统计意义；在简单的实际情境中，应用统计图表或百分数，形成数据意识和初步的应用意识。

《课标（2022年版）》设置了“学业要求”模块，关于百分数的要求是：能在真实情境中理解百分数的统计意义，解决与百分数有关的简单问题。

由此看出，《课标（2022年版）》把百分数与平均数一起当成统计量看待，其重心转向了数据分析与应用，突出百分数的统计意义。

二、年段衔接点

百分数既然已经作为一种统计量，那么我们不妨基于“统计与概率”的视角，梳理这一领域的相关内容以及教学目标的前后联系。

第二学段（3~4年级）：理解平均数的意义，会用平均数解决问题；形成初步的数据意识。

第三学段（5~6年级）：理解百分数的意义，了解随机现象发生的可能性；形成数据意识和初步的应用意识。

第四学段（7~9年级）：经历利用样本推断总体的过程，能够计算平均数、方差、四分位数等基本统计量，了解频数、频率和概率的意义；形成数据观念、模型观念和推理能力。

由此看出，百分数意义的教学不仅要关注其与分数、比、倍等相关概念的关联与对比，厘清百分数概念的内涵，更要借鉴平均数概念的学习经验，设计指向数据比较与分析的统计活动，让学生在对数据的分析处理过程中感悟百分数的统计意义，为第四学段方差等统计量的计算与运用积累方法和经验，形成数据观念。

三、疑难问题与策略建议

1.怎样基于现有教材准确把握百分数的统计意义？

（1）识别逻辑关系。

现行教材呈现了前后关联的三个片段：例举生活中几个常见的百分数；揭示百分数的名称及意义；阐释具体情境中百分数的意义。应该说三个片段之间的逻辑关系是紧密的：呈现多个生活实例→让学生尝试解释其含义→感受百分数的意义。教材的编排遵循的是归纳逻辑，但是忽略了百分数的产生背景，学生无从体会百分数产生的必要性，缺少百分数概念的再创造经历。

（2）追溯概念起源。

分数、负数等都是因为数系扩充的需要而产生的，而百分数却源于统计过程中的数据分析，例如要衡量哪种药品对某种疾病的治愈率更高，就需要有一个能反映一组数据特征的量。从这一点说，百分数与平均数都是为了描述一组数据的特征，作为统计中的代表量而存在，例如，篮球运动员投篮的命中率、果汁中不同成分的含量等。概括地讲，百分数产生于统计的需要，与实际应用紧密结合，是两个数量基于除法关系得到的结果。

（3）厘清关联概念。

百分数是比的下位概念，可以反映部分与整体两个量之间的比率关系，如出勤率、合格率等；也可以表示存在并列关系的两种量之间的比率，如商品实际售价是原价的70%、实际产量比计划增产11.2%。

百分数与分数之间既有联系，又有区别。百分数表示比率，没有单位，不能表示具体数量，而分数既可以表示一部分与另一部分的关系，也可以从数值意义上表示一个量。从运算角度来看，百分数与分数、小数存在着表征形式上的关系，所以百分数与整数、小数、分数的四则运算，都能够转化为分数或小数的四则运算，但是究其实质，百分数仍然作为一种统计比率的指标而存在。

2.怎样帮助学生全面理解百分数的应用价值？

虽然百分数从“数与代数”领域移至“统计与概率”领域，但是仍然表示一个数是另一个数的百分之几，其意义并未改变，发生改变的是应用范围与价值的扩展。以前百分数的应用侧重于计算和解决实际问题等一般应用，现在则凸显了统计意义，教学中就要更多地关注用百分数表达数据信息，增强数据分析能力。

（1）弱化一般应用价值。

在以往的教学中，我们认为百分数是分数在分率意义上的一种应用。例如，“求一个数是另一个数的百分之几”与“求一个数是另一个数的几分之几”解题方法并无区别。与之类似的还有：求一个数的百分之几是多少；已知一个数的百分之几是多少，求这个数；求一个数比另一个数多（或少）百分之几……解决这些问题，只需把题目中的百分之几看成几分之几，是对分数问题的再应用。

（2）保留商业应用价值。

从生活实际和学习经验出发，教材中选编了纳税、利息、打折等商业问题。这些都是经济生活中的重要问题，能帮助学生积累解决问题的经验，为未来的生活、工作奠定基础。尤其是打折问题取材于购物活动，是学生在现实生活中接触最多的问题。这类问题变化较多，如折上折问题、多件才打折的问题、买几送一的问题等，对于感受百分数的应用价值，激发学习兴趣起到了促进作用。

（3）增强统计应用价值。

《课标（2022年版）》中，百分数从一种数到一种统计量，从方便比较到数据意识，将其作为一种统计数据，用来进行比较和分析。

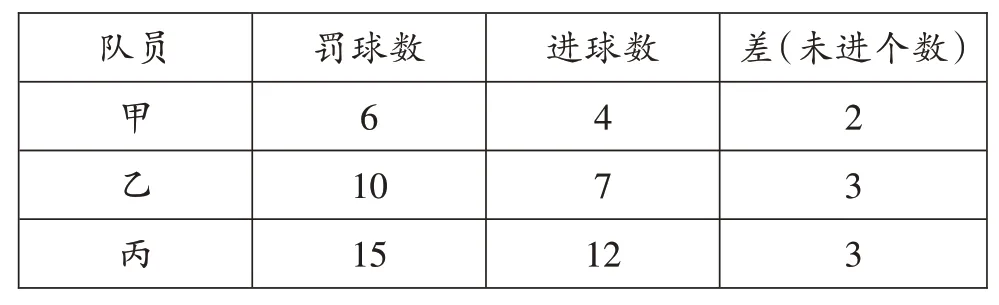
例如，教学中创设足球比赛罚点球的情境，引出“谁来主罚这个点球”的任务。出示收集到的三名队员在某赛季的进球数，让学生从三名队员中选择。学生认为，只根据进球数无法作出判断，需再出示三名队员的罚球数。经过讨论，学生觉得最科学的方法不是比较罚球数与进球数的差，如下表：

?

从表中的数据看，甲虽然未罚进的球只有2个，看似失误最少，但是很显然他的罚球水平并不高。最终，学生认为罚球水平的高低应该看进球数与罚球数的比率，即命中率。教师接着追问：派命中率最高的队员去罚点球就能保证命中吗？学生稍加思索，纷纷摇头：在球场上，实际命中的情况是不确定的。从层层比较与追问中，学生渐渐理解了百分数表示的是随机情境中的倍比关系，具有不确定性。上例中，通过表格中数据的对比，学生感觉到：数据量越大，百分数呈现的某种规律的可信度越高。

3.怎样做才能让学生体会“百分数是一种重要的统计量”？

在以往的教学中，学生普遍认同“百分数是一种特殊的分数”，是分率意义的应用。《课标（2022年版）》将重点转向用百分数表达统计数据，感受百分数的统计意义。那么，怎样促进学生对百分数统计意义的理解，体现百分数在数据刻画方面的独特价值呢？

（1）在真实统计中引出。

只有充分经历数据的收集、整理和分析过程，学生才能感受百分数的产生是解决现实问题的需要。

首先，经历数据采集的过程。例如，让学生调查本年级学生体质达标率，可以通过问卷调查收集本年级达标学生数，计算出达标率；也可以调查本班的达标率，再以此为样本推算本年级的达标率。由此让学生利用课外时间展开统计活动，并启发学生比较两种方法各自的优点和不足。

其次，展开数据分析的过程。在调查收集的基础上，组织学生对得到的百分数进行理性分析。例如，调查得到本年级学生的体质达标率后，可以与全市平均水平比较，与国家体质标准比较，客观分析原因，提出改进建议。还可以拓展视野，收集经济、社会等领域的数据，例如，收集商家在节假日促销打折的情况，分析购买行为，提出消费建议。

（2）在主动比较中生成。

百分数和分数一样，都可以表示两个数量之间的倍比关系，而且对两个量关系的表达，标准统一，便于比较。

有关研究结果表明，百分数概念的建立，一般要经历这样的逻辑发展过程：单一维度的量比较（不可行）→综合考虑两个维度的量→作差比较（不可行）→作商比较→通分，比较同分母分数的大小→数据太多，通分不方便→以100为公分母→形成百分数的符号表征。

例如，我们设计了关于本校六年级学生近视率的调查统计活动，让学生设计方案，收集数据。在学生求出近视人数占总人数的几分之几后，我把统计数量扩展到3所学校，提出问题：想知道哪所学校六年级学生视力情况好一些，应该怎么办？学生提出先通分，再比较。接下来，出示全市30多所学校六年级学生的视力调查数据，学生感悟到通分的公分母太大了，萌生了“找一个统一的标准”的想法，逐渐形成取统一的较小的公分母100的设想。为了避开原有分数中分子、分母均为整数的要求，将分母100改写成“%”的形式，百分数概念由此建立。

教学中，为了充分体现百分数对数据刻画的作用，课堂上呈现的数据从少到多、从简单到复杂，学生逐渐体会到通分的方法存在局限性，从而产生寻求统一标准进行比较的需求。像这样，从解决问题的需要出发，巧妙设置认知冲突，激发学生主动比较和判断，体现百分数对数据刻画的优势。

（3）在梳理关系中体会。

百分数作为对两个量之间关系的表达，在实际生活中有着广泛的应用。教师在课前会给学生布置“寻找生活中的百分数”的任务，以进一步加深对百分数表示两个数量之间关系的理解。在交流中学生发现，百分数既可以表示部分与总量的关系，也可以表示并列的两个量之间的关系。

例如，同样是关于近视人数的调查，如果是统计近视率，反映的是近视人数与总人数的关系，百分数不可能超过100%；如果统计某班近视人数的增长率，关注的是增加的人数与原有人数，这里的百分数有可能超过100%。精心选择同一主题下揭示不同关系的现实素材，有助于学生进一步理解百分数意义的本质。

（4）在感受随机中深化。

百分数不仅可以表达确定数据，也可以表达随机数据。笔者曾经听过《百分数的意义》一课，对“制订跳绳标准”这一环节印象深刻。

课上，教师提出问题：以六年级男生为例，要制订跳绳标准，你能设计方案吗？各个学习小组的方案中包含抽样调查、收集数据、整理数据、确定等级等，意在借助数据解决问题。随后，教师提供了100名男生1分钟跳绳数量统计表，将这些数据排序后，有的小组把第50名的数据作为达标线，表示有50%的学生达标。有的小组质疑，认为这样的标准定得太高了，将第75名学生的跳绳数据作为达标线，目的是让75%的学生达标。还有的小组划分了优秀、良好、合格和不合格四个等级，比例各占25%，这样细分标准的目的在于更好地调动同学们跳绳的积极性。最后出示国家跳绳标准，学生进行对比。

跳绳的个数虽然是变化的，但如果收集的数据足够多，就能发现某种规律，从而选择合适的百分数解决达标线问题。实际上，生活中有许多类似的例子。例如，用百分数比较本地不同季节的空气质量问题，虽然数据在变化，但是如果收集的数据足够多，就能分析出影响空气质量的相关因素，并研究出对策。

资料存盘

《课标（2022年版）》在“课程目标”中提出，会用数学的语言表达现实世界；在义务教育阶段，数学语言主要表现为：数据意识或数据观念、模型意识或模型观念、应用意识；能够感悟数据的意义与价值，有意识地使用真实数据表达、解释与分析现实世界中的不确定现象。

在“学段目标”的第三学段（5~6年级）中提出，理解百分数的意义，了解随机现象发生的可能性。

在“课程内容”中指出，数据的收集、整理与表达包括数据的收集，用统计图表、平均数、百分数表达数据；结合具体情境，探索百分数的意义，能解决与百分数有关的简单实际问题，感受百分数的统计意义；在简单的实际情境中，应用统计图表或百分数，形成数据意识和初步的应用意识。

在“学业要求”中进一步提出，能在真实情境中理解百分数的统计意义，解决与百分数有关的简单问题；能在认识及应用统计图表和百分数的过程中，形成数据意识，发展应用意识。