数学教学中培养学生观察力的策略研究*

董晓梅 林芳羽 牟 丹 张丽春

（北华大学 数学与统计学院 吉林吉林 132013）

一、观察能力在数学学习中的意义

一个人如果对周围的事物不能进行系统周密的观察，就不能得到大量的感性材料，思维就会缺乏厚实的基础[1]。

在数学中，观察活动不单单是局限于观察数学图像、图形。随着学生抽象能力的提升，数学的概念、定义、公式也是观察的重要对象。认知的起点是感知，数学中的观察就是感知一切的数量关系和空间形式[2]。

观察是记忆、想象、创造等思维活动的前提。因此，观察力是学生主动发现问题，解决问题，实现自主学习的基础能力。良好的观察素养能够帮助学生形成系统完善的思路，能够为学生提供分析解决数学问题的动力，能够促进学生综合素质的全面发展[3]。而教师培养学生的观察思维，提升其观察能力，塑造其观察品质是教师培养自主学习型人才的第一步。

二、观察力的培养策略

1.发挥元认知的期望、调节功能——有目的的观察

数学中的观察是有目的、有选择的感知过程[4]。观察水平的高低与思维的参与程度有关，而人的思维往往需要元认知的控制。元认知给予观察前的期望、观察过程中的调节及观察后的反省。

在数学解题过程中，观察的目的更多的是要建立起已知和未知之间的桥梁，找到由已知推未知的捷径。如下题：

例1：已知函数f(x)=m x2+(m-3)x+1的图像与x轴的交点至少有一个在原点右侧，则实数m的取值范围是？

解析：可以观察到m是函数的系数。如何将系数的取值与函数的交点建立代数关系？带着这个目标，观察已知条件。

教师要帮助学生明确观察的主要矛盾，提高学生锁定观察范围，判断核心目标的能力，强化学生的元认知期望、调节能力。

2.遵循科学步骤，找寻观察线索——有顺序的观察

观察是顺序知觉的过程[5]。因为观察对象具有多层次的特征，人的认知也遵循着层层推进的逻辑顺序。

3.抓住对象的特点，内在关系——尊重客观属性

观察是对客观事物进行能动反映地认识过程。在面对复杂事物或者已有经验不足以支撑对观察对象的理解时，观察的结果往往不会客观的反映观察对象。如果观察的心态不稳定，也会影响学生的观察结果。不全面地分析或想当然地增加一些内在联系再或者产生错误的理解是学生经常存在的问题。

例3：如图所示，几何体的左视图是（）。

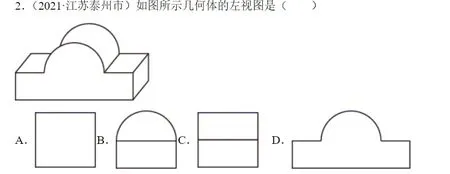
解析：如果学生对“半圆柱体的侧视图是长方形”这一客观现象没有稳定认知，就会受半圆的干扰，错误理解成B选项。

解：C

教师应尽量呈现直观，剖析原理；通过传授一定的观察方法和经验，如特殊到一般观察法、比较观察法等，来帮助学生发现对象的客观属性。同时，教师需及时纠正学生错误的认知，引导学生反思出错的原因，培养尊重客观事实、严谨求证的品质。

4.整合新旧知识的联系——组块化观察

若观察对象复杂程度高，会产生较大的认知负荷，导致思绪混乱，视觉疲劳。这需要整合新旧知识的联系，组块化处理观察信息。

组块化处理是指根据已有经验，对观察对象识别、分类，以较大的单元加工信息、进而做到迅速、有意义的观察。这种加工处理方式能帮助我们在观察中识别大量的信息，以深层的方式来表征问题，把握实质。

解：C

教学中，教师要帮助学生梳理、总结已有经验，培养良好的抽象能力对观察对象进行意义组块，分类表征不同情况下的可能性。

5.结合必要的推理、证明——弥补观察的局限

首先，由于观察对象的复杂性，人生理感官的局限性，能借助的工具也有历史制约性，观察的结果并不能作为数学事实的严格论证[6]。

再者，学生不能过多地依赖观察，教师如果过度地呈现直观，往往阻碍学生的抽象思维发展，养成惰性思维、刻板思维。基于以上两点，观察还需结合必要的空间想象，抽象理解，结合严谨的推理和证明。

教师自身应具备多元的科学素养，帮助学生运用推理证明来克服观察的局限性，得出全面、客观的结论。同时，培养学生用发展的眼光进行观察，敢于质疑，发现、发展新知识。

三、数学观察的品质要求

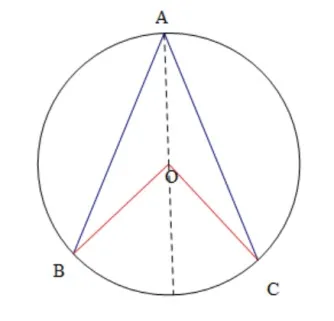
观察是我们与生俱来的本能。但是，要达到数学教育的育人目标，学生还需具备全面的观察思维、持续的观察耐力，做到多维的信息挖掘，深刻的本质概括，自动化的直觉感知。

1.全面的观察思维

此外，学生要有能力思考可以凭借哪些线索，找全对象，进行多次观察后总结共性。例如，学生观察归纳矩形的性质时，如果观察的只是正方形，便会把对角线互相平分，四边相等的性质延伸到矩形的性质里。

常见的全面性观察思维还有逆向思维、推广思维。例如，通过观察性质思考其逆命题是否可做判定定理？又如，观察到相似三角形的边长成比例时，要考虑到面积是否也成比例？

当然，一个人的观点往往是片面的，学生还需要具备交流能力，在合作探究中，取长补短，丰富思维。

2.持续的观察耐力

随着数学学习的深入，数学观察对象会越来越复杂。一次或短暂的观察往往是不能得出我们想要的数学结论的。

学生持续的观察力、强烈的求知欲是关键的观察品质。教师应不断地鼓励和引导学生，让其形成较高的自我效能感和成就动机。

学生在学习数学时，是否具有较好的耐挫力和对自己的信心决定了学生观察时的耐力水平。现在，大多数学生缺乏观察的耐力，一是因为经授学习的挫折后得不到及时肯定；二是基础薄弱，学习动力下降；三是教师采用应试教育方式，只注重做题速度，忽视给学生留足发现学习的时间。

在观察活动中，教师应该及时地肯定学生的进步，并运用支架式教学逐渐引导学生深入观察。

例如，在学习勾股定理中，教师要给学生一定的时间进行自主观察，动手拼接“赵爽弦图”（右图），一步步地引导学生自主证明勾股定理。

3.多维的信息挖掘

事物具有多方面的矛盾，围绕观察的目标，尽可能地反映事物的多个方面和多种规律是学生客观感知的必要素养。数学学习中，往往需要把各个模块学习的知识综合应用起来，如下题：

例6：如图所示，一只装有半杯水的圆柱形水杯，将其倾斜使杯底与水平桌面成30°，此时杯内水面成椭圆形，此椭圆的离心率为（）。

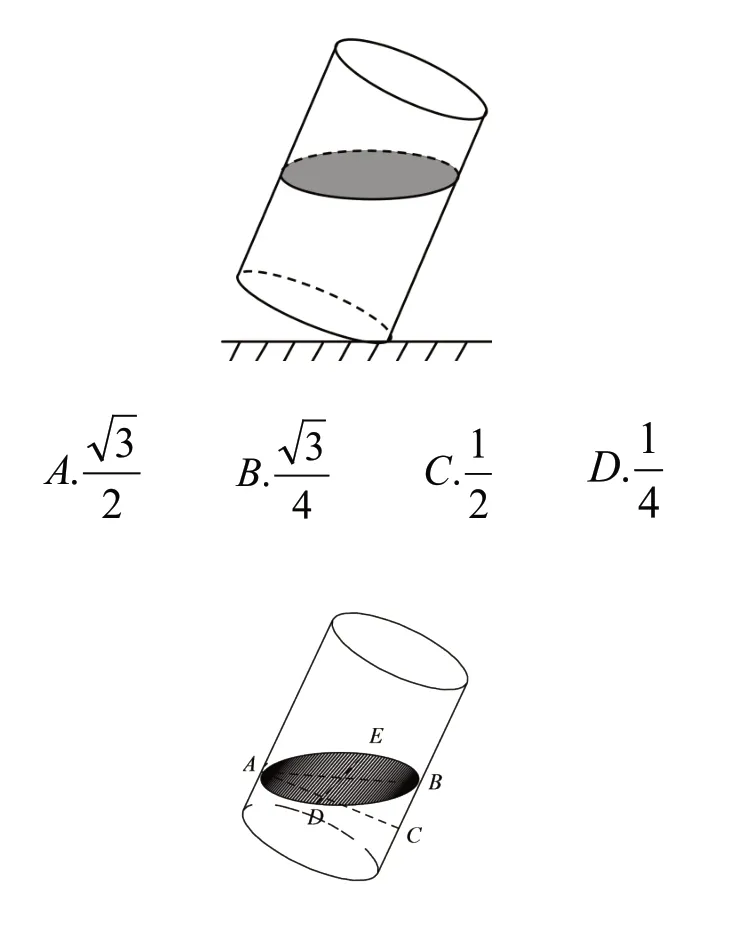
解析：观察上图，必须把倾斜角30°用到椭圆水面中去。离心率必然离不开椭圆的长轴和短轴。在图中，要把这些信息挖掘出来。通过构造新图形，找出等量关系。

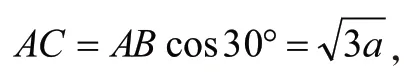
在观察中，能提取的信息的多少还取决于学生原有的认知结构是否稳定。如果学生对于已有的知识掌握得不牢固，会限制对观察对象内在规律和联系的发现。在观察中，教师不仅要训练学生的多维度兼顾能力，而且还要帮助学生查漏补缺，夯实基础。

4.细致的发现探究

细致的观察是发现学习的前提。学生要有通过观察发现别人发现不到的点的优良品质，锻炼在解题时，能找出隐藏的数量关系，确定最优的解题路径的能力。例如，观察学习导数时，能否借助导函数的图像走势，还原原函数的斜率，

不论学生的发现过程或者发现结果是否在教学范围内，只要是有助于学生发展的，教师都应该进行肯定。例如，上文中提到的，教师除了引导学生借助杨辉三角理解二次项定理之外，还应鼓励学生仔细探究其它的规律，如细心的学生还能发现杨辉三角的第二层是自然数列，从左边数第三斜纵列相邻数字相加可得方数数列。

5.深刻的本质概括

观察是形象思维和抽象思维的结合，形象思维帮助把握形象构造，抽象思维帮助分析性能关系。把观察中获取的信息整合加工后，抽象出其本质的属性和内在的规律是数学观察的重要过程，也是较难的一步。

例如，在学习圆的标准方程时，先通过观察得出圆上的所有点满足到圆心的距离相等的性质，联想到两点间的距离公式，进而抽象出圆的标准方程。

深刻的本质概括是观察活动促进思维发展的阶梯。信息经过抽象概括后形成知识，一个个知识单元丰富着学生的知识结构；而知识建构越丰富、越深刻、越稳定，学生的迁移应用能力就越强，学习新知的能力也就越强，这是一个螺旋上升的过程。

6.自动化的直觉感知

当学生对某一事物具备大量的表征后，再观察与该类事物相关的新内容时，就可以进行组块化处理，快速感知信息。

例如，三视图之间的识别转化，函数表达式间的变形还原，斜二测直观图与原图间的转化等都对学生有较强的直觉感知的品质要求。

研究表明，人脑当中存在两种不同的信息加工系统，即意识加工和无意识加工。而无意识加工是指不受固定的逻辑规则的约束，由思维主体自觉领悟事物本质的思维活动[7]。

学生具备一定能力后，教师应尽量放开对观察的期望限制，使学生除具备锁定观察核心的能力以外，还具有跳出观察程式，捕捉创新机制的能力[8]。在教学过程中，教师经常会看到，学生会有自创的简便解题技巧，快速的对错判别方法，这些往往更有效。