数学的美学特征及其培养策略*

林芳羽 董晓梅 牟 丹 张丽春

（北华大学 数学与统计学院 吉林吉林 132013）

数学与艺术，一个因其严密的抽象逻辑见长，一个充盈了人们的心灵盛宴。近代科学家开普勒曾说过：“数学是这个世界之美的原形。”数学展示的原始过程是将冰冷的美丽转化成火热的思考。所以说，数学是有温度的，严密的逻辑和理性的推导也是一种严谨美，数学与美学密切相关。伯特兰·罗素 用以下文字表达他心中数学的美；“数学，正确看待时不仅具有真理，还具有至高的美—一种冷而严峻的美，一种毅力不摇的美，如雕塑一般，一种不为我们软弱天性所动摇的美。”数学中的美学特征和教育意义也逐渐被人们重视。随着基础课改的不断深入，只传授学科基础知识的形式已无法适应改革的需要，教育过程中应更体现教育的育人价值，需要我们渗透数学的美学价值和应用，以达到培养学生美育的要求。那么，到底什么是数学美学特征？教学中又该如何发掘和应用呢？

一、数学的美学特征

1.简易美

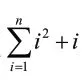
2.对称与和谐美

“对称”一词来自希腊，意思为“和谐”“美观”。数学上的对称美则更加追求其和谐的美感。这种例子十分常见，如我们接触过的等腰三角形、矩形、圆等。除了在几何方面的对称，代数式子中也能凸显对称的特点，在高一学生接触到抽象函数和奇偶函数后，能从式子上发掘对称关系，又和图像结合，数与形都随处可以发现对称的影子。再比如，高中接触的二项式定理的内容，二项式的展开形式就是一种和谐的美，而构成的杨辉三角则更将数的对称拓展到形的美观。和谐美也更加倾向于形式上的美观，黄金分割就是数学上一个经典和谐美的表达。此外，在小学教学中，分数的均分所体现的除法思想，就是通过图像平均分配的具象思维来体会均分的含义，这也是一种和谐美的展示，相反，如果任意的分割，则会打破这种和谐。在离散数学中，数学形式和结构的对称性、离散数学的命题关系中的对偶性、离散数学的方法中的对偶原理方法都是对称美的自然表现[3]。

3.严谨美

数学的严谨性则是数学本身最具有特色的体现，纵观数学发展的四次高峰，在以希尔伯特为代表的现代公理化时期，给人们留下了许多数学精品。特别是布尔巴基学派，更将形式主义推向了新的高峰[4]，数学是由一系列公理加以推理形成的，经过了严密的步骤和不断推演形成了公式和定理。这种完备的公理体系和逻辑推理过程正是数学严谨美的体现。此外，数学的严谨性还体现在符号的严谨性。数学的内容也一直和严谨性相关。正是数学的严谨性，使得数学工作者求真务实，敢于追求真理的品质。这就是数学美的严谨价值所在，也是数学的魅力所在。

4.抽象美

“抽象”源于拉丁文中“abstractic”，本意为“排出” “抽出” 之意。抽象性也是数学的基本特质之一。首先，数学的抽象性包含很多方面，数学部分的研究内容是抽象的，研究方法是抽象的，数学思维也是抽象的，抽象性是数学的最基本的性质.数学家所研究的是抽象的事物，他们所采取的研究方法也是抽象的方法。其次，还在于数学原理的通用性和普遍性。这其实就是数学抽象，数学抽象从数量关系和空间形式抽象出数学问题的本质。ƒ（χ+2）=ƒ（χ-4）中。我们能从这个抽象的式子背后，发现其周期T=6，而从ƒ（χ-2）=ƒ（4-χ）中，我们能得出该抽象函数的对称轴为X=1。这便是一种抽象的美感。

5.奇异美

奇异，意味着：一是新颖，具有其独特的特性；二是新奇，令人赞叹的美。数学中的奇异美，常因其外形结构奇特，使得很多数学热爱者去探索数学美背后所蕴含的数学公理，看到了由数学所构成的奇异美感的世界，无疑推动了数学的进步。[4]例如，著名的狄利克雷函数也具有一系列奇异性质：没有解析式、不单调、不连续，不存在极限、没有最小正周期等。又如，153 是一个极为普通的数，但却有许多有趣的性质：1+2+3+…+17=153，1!+2!+3!+4!+5!=153，这也是一种奇异美。离散数学中的集合可以表示为 {1，2}，（-1，2000），集合中的数字可以是随意地让我们感觉到无从下手的奇异美[5]。

二、对审美教育的培养策略

无论是数学的美学特征，还是数学的审美教学，在进入课堂一线上，其实际运用效果总是差强人意的。那么，如何在教学上具体凸显其美学特征，培养学生。

1.了解数学文化，融入思政教育，丰富美学内涵

算意识和实际操作。从《周易》到八卦随着教学改革的发展进程，越来越多的数学教师开始重视学生的学科知识多元发展的融合，学科核心素养概念的提出更是在之前的教育理念上有了质的飞跃，其突出强调个人修养、社会关系、家国情怀，更加注重自主发展、合作参与、创新实践。因此，教师有必要在课堂之中融入思政教育。徐利治曾说过：“兴趣和才能是互相促进的.而兴趣的培养和发展，其最有效的途径就是要多读些富于启发性的数学史书和数学家故事[6]。”因此，可以将思政教育与数学文化相融合，实现其精神价值、德育价值和审美价值。

2.化繁为简，简则易知，易则易从，体会数学的简易美

正所谓，人人都有爱美之心。而数学结构形式（包括公式与各种关系 ）间的简单性、规律性与对称性等正好是美的象征，想要追求简易美，在教学上要培养学生勤于计算的习惯，寻找问题的突破口，体会化繁为简数学美的过程。这也契合数学核心素养中对于数学运算能力的要求。

比如，在高中讲解三角函数的问题时，我们经常要去求函数的值域、周期、相位等。针对问题的第一步就是化简，但现实情境中，学生往往不知道如何下笔，除了要强化学生的运算能力、数据处理能力，还要培养学生善于观察的习惯，最重要的是教师要加以引导，将问题简单化、思路明晰化，才是最后简易美的目标。下面笔者拿具体的公式来举例：

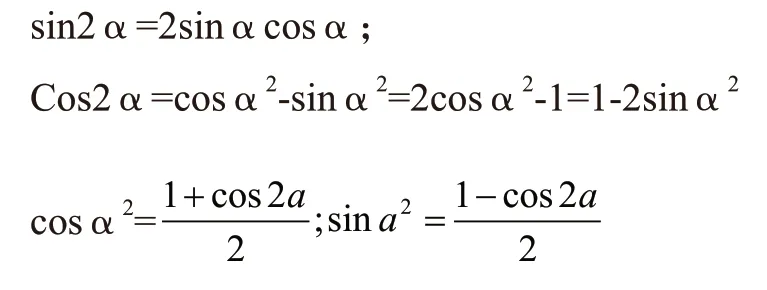
由于该章教学在初升高的第一个学期接触，难免有些学生对此觉得难以掌握，同时，这部分内容还需考察学生的识记及运用能力。在接触大量的公式中，如二倍角公式，半角公式，万能公式觉得难以掌握，即便是背会也不会应用，所以教师需要带领学生观察公式的特点。通过观察发现，在公式中普遍存在的一个规律：“降幂升角”即a→平房顶；2a一次项，所有的倍角公式可以由单角平方项进行互推。这样讲解的优点是：

第一，帮助学困生理解公式变换的思路，由降幂升角的特点就可以选择公式，同时可以检查自己化简步骤是否有误，可以避免一些运算上的失误。

第二，减轻了记忆的负担，通过公式的推演极大地减少了识记的内容。

第三，掌握了选择公式的计算方法之后，便可以通过联系进行初步应用，掌握了化繁为简的能力，为后续学习提基础。

因此，简易美往往是数学解题中寻求答案的重要体现，简易的数学步骤更能增强学生的解题能力。教学中要教授学生具体的学习方法，加以训练，加强学生的动手实操能力，从而感受简易美。

3.注重“挖掘—体验”的教学过程

教学的过程是教与学的互动过程。教师在教授的过程中需要制定教学设计，所以，数学的美学教育也需要在教学过程中进行完备巧妙的设计，挖掘在前文的数学文化中已有涉及，在前期引入上发掘教材中的审美元素，创设情境，充分地利用好教参，培养学生审美的感知力。

数学解题过程中，强调“一题多解”“一题多变”就有着重要的美学意义。在某种程度上说，他们是数学审美意识的具体应用。通过解题过程中数学知识与数学方法的灵活多变，最终又能归于统一与和谐，学生就能深切地体验到数学的思维之美，变形之美，猜想之美，探究之美。

在教学过程中，重视直观的现象教学，利用多媒体教学，向学生展示数学的动态过程，体会数学形成的动态美；重视数形结合的应用，在转化中体验数学美。

4.培养学生勇于探索的品质，落实数学美的深层次表达

除了带领学生感受基本的美学特征以外，还需要达到数学教学美的四个层次，张奠宙曾阐述过数学美有四个层次即美观、美好、美妙、完美。四个层次逐步递进，从形式上的美观到最后追求真理，追赶完美。

美观。这里的数学美则更加指向形式上的追求，体现为对称、和谐、简洁，给人的感官带来美丽简洁的感受。这是数学美的直观表达形式。

美好。如果说美观是数学外在形式的美学表达，那么，美好则是其内容上的丰富和正确性，仅仅有形式上的美观不一定就是正确的，也是不满足数学的科学性和真理性，所以这就是数学美的第二个层次。

美妙。主要在于妙字，是一种出乎意料的结果，也可能解题中一种新路径、新发现。这种美妙往往会给学习者带来一种体会真理的快乐，所以，在教学中，教师应该鼓励学生发散思维，不拘泥局限思维，鼓励学生自行去发现解题的新方法，靠学生自行发现往往会给学生带来最深的印象。我们可以去看这样一道例题：

例：（2019·全国卷Ⅲ）设χ，у，z∈R，且χ+у+z=1.求（χ-1）2-（у+1）2+（z+1）2的最小值。

思路1：根据三维柯西不等式

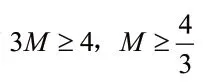
思路2：利用三项平方和展开式可得，

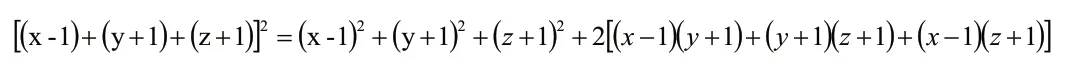
延用一步平方和的展开公式进行替换，也能算出来最后答案。

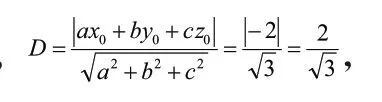
其实，我们通过观察三种解法，会发现运用柯西不等式解决该题是最为简单的，但由于教材版本和地域的不同，有些学生对柯西不等式得掌握是比较模糊，或是掌握的是二维，无法类推到三维。因此，可以寻求多样化的解法，解法2中是常规解法，利用了一步基本不等式进行带入。最后，我们观察同学做题时还发现此题可以类推到直线的距离公式当中，也是一种新颖的路子，可以拓宽学生的思维，引导其对知识的迁移和运用。

完美。完美是具有科学，严谨，追求完备极致表达是数学美的最高表达。数学史上有很多数学家为了追求数学真理不断地进行计算，一便便推演，终于得出了正确的结论。正是这些人孜孜不倦的努力追求，才有了数学发展史的一次次飞跃。完美则体现了数学美学的最高涵义。所以，我们在数学学科上更要不断勇攀高峰，拓宽思维，严谨务实，追求美的最高表达。