怎样画一个相等的角
2022-01-25 06:00:53于瑞云
教学月刊·小学数学 2022年2期
于瑞云


在做练习题“画一个与已知角相等的角”的过程中,学生可以巩固量角与画角的知识,体验它们之间的联系。具体可通过尝试、说理、检验等活动完成这样的练习。
一、出示习题,独立尝试
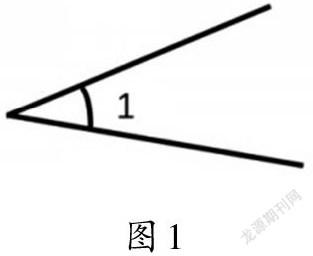
教师出示∠1(如图1),请学生独立尝试画出与∠1同样大的角。
二、交流反馈,形成路径
(一)用“量角器”画角
1.画一画:运用量角器,怎么画相等的角?
2.说一说:先量角,再画角。
3.量一量:两个角是否相等?
(二)用“直尺”畫角
讨论:如果只有直尺,能画出相等的角吗?学生尝试后重点交流其中的3种方法。
1.画延长线,找相等角。
方法:把∠1的两条边延长(如图2),即可画出与∠1相等的∠3。
讨论:为什么这两个角相等呢?
说理:因为∠1+∠2=180°,∠3+∠2=180°,所以∠1=∠3。
补充知识,形成结论:如果一个角的两边分别是另一个角两边的反向延长线,且这两个角有公共顶点,那么这两个角是对顶角,对顶角相等。
2.运用平移,画相等角。
方法:通过边的平移可以画出与原来的角相等的角。
讨论:怎样平移才能画出相等的角?
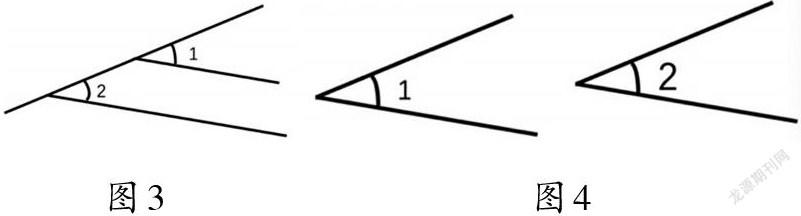
梳理:将一条边延长,另一条边在延长线上平移,就可以画出相同的角(如图3)。也可以将两条边同时平移画出与原来的角相等的角(如图4)。
3.借开口度,悟相等角。
方法:角的大小跟张开的大小有关,只要张口度一样,角就相等。
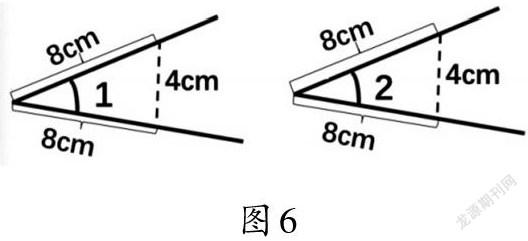
讨论:如果图5中的两个角“张口处”线段的长度都是4厘米,这两个角一定相等吗?什么情况下能保证两个角是相等的?
结合度量,得出结论:如果在距离顶点同样长度的地方连线,得到“张口处”的线段长度相等,这两个角就一定相等(如图6)。
如上,在画一个相等角的活动中,学生充分调动已有的知识和经验,通过自主画图,交流反馈,发展了探究能力和推理能力。
(浙江省杭州市富阳区永兴小学 311499)
猜你喜欢
中学生数理化·七年级数学人教版(2020年2期)2020-02-04 06:37:30
学苑创造·B版(2019年10期)2019-11-22 14:46:37
小学教学参考(数学)(2018年9期)2018-09-28 05:26:42
——以“画角的复习”教学为例
辽宁教育(2017年23期)2017-12-06 07:08:51
中学生数理化·七年级数学人教版(2016年1期)2016-05-30 22:49:43
中学生数理化·七年级数学人教版(2016年1期)2016-05-30 10:48:04
学苑创造·B版(2015年11期)2016-01-13 09:38:31
中学生数理化·七年级数学人教版(2015年1期)2015-05-30 14:12:43
中学生数理化·七年级数学人教版(2014年1期)2014-06-20 00:20:06
东方青年·教师(2013年5期)2013-04-29 08:24:14

