基于公理化模糊集合的TOPSIS 多属性决策方法

王 虎，潘小东，康 波

（西南交通大学数学学院，四川 成都 611756）

1981 年，Hwang 等[1]提出了基于理想点原理的TOPSIS 方法，经典的TOPSIS 方法一般用于以确定的实数作为属性值的多属性决策方法。1965 年，Zadeh[2]首次提出了模糊集合的概念，将数学理论与应用的研究范围从精确性问题拓展到了模糊性问题。1970 年，Bellman 等[3]首次基于模糊集理论建立了模糊决策的基本模型。此后，基于模糊集合以及模糊集合的各种扩展模型的模糊决策方法被相继提出。胡辉等[4]在2007 年提出了基于区间直觉模糊集的TOPSIS 多属性决策方法，将属性值由确定的实数替换为区间直觉模糊数，希望解决属性难以用准确值表示的TOPSIS 多属性决策问题。2017 年，王应明等[5]提出了基于前景理论的犹豫模糊TOPSIS 多属性决策方法，考虑到实际决策过程中决策者的犹豫心理，选用一组语言值来对属性进行描述。2018 年，张文等[6]提出了基于区间犹豫模糊语言集的TOPSIS 多属性决策方法，使用了区间犹豫模糊语言数来表示属性值，能够更加细腻、准确地描述事物的模糊性。

在模糊多属性决策过程中，备选方案的属性值往往需要使用定性的评价自然语言去描述。对评价自然语言的处理，目前常用的第一种方法是用模糊数、三角模糊数、直觉模糊数等来表示语言值[7−11]；但存在的问题是，模糊数或者扩展的模糊数的隶属度的确定存在较大主观性，并且这些模糊数与决策者在决策过程中所使用的评价语言值很难建立合理的对应关系。第二种常采用的方法是把一组语言值用集合S={sa|α=−t,···,−1,0,1,···,t}表示，并且通过集合S中元素的下标来定义对应语言值之间的序关系、集结及相似度等计算的算子[12−16]。例如，Rodríguez 等[15−16]根据犹豫模糊集的背景，提出了用一组语言值来作为属性值，并且给出了犹豫模糊语言的序关系以及集结的算子，用于多属性决策问题。语言值以离散的形式给出，它们之间经过相对应的集结算子运算以后，生成新的语言值可能不能与初始语言集中的语言值相对应，引起初始信息的流失。

2018 年，Pan 等[17−18]从模糊现象的本质和特征出发给出了模糊集合的公理化定义，从整体或全局的观点给出关于模糊概念的新认识。公理化模糊集合是定性评价自然语言的数学模型，使Zadeh意义下的模糊集严格化、明确化、清晰化。在公理化模糊集合的框架下，模糊集合能够与评价自然语言值之间建立良好的对应关系。

综合上述分析，本文以公理化模糊集合作为基础讨论属性值用评价语言值表示的模糊多属性决策问题。基于评价自然语言值集建立模糊划分，并基于模糊划分生成公理化模糊集。对不同论域下的属性值对应不同的模糊划分，决策过程中直接使用公理化模糊集来进行决策建模计算。结合经典的理想解TOPSIS 方法，本文建立基于公理化模糊集合的TOPSIS 模糊多属性决策方法。

1 公理化模糊集合的基本理论

下面我们首先给出模糊划分和公理化模糊集合的定义。

定义1[17−18]设U=[a,b]⊂R,U上的一个模糊划分指的是具有如下形式的对象：

2 公理化模糊集合的序关系和距离

2.1 公理化模糊集合的序关系

在模糊多属性决策理论中，模糊集合的序关系扮演着非常重要的作用。如果各方案的最终打分是用模糊集合来表示的，那么就需要用一种方法来对模糊集合进行排序。

为了定义模糊集合的序关系，下面我们首先将同一模糊隶属空间中的模糊集合转化为实数，然后再根据所得到的实数值的自然序对模糊集合进行排序。

定义3设定义A的模糊均值mv(A)为

其中[a,b]为公理化模糊集合A的论域。

定义4设，定义上的序关系≤为：A≤B当且仅当mv(A)≤mv(B)。

例1用语言评价集{好，中，差}来评价某个班级学生综合测评分数的好坏，设论域为[0,100]。用模糊集合A1表示评价语言“差”，用模糊集合A2表示评价语言“中”，用模糊集合A3表示评价语言“好”，它们的隶属度函数分别定义为：

身高隶属度函数如图1 所示。

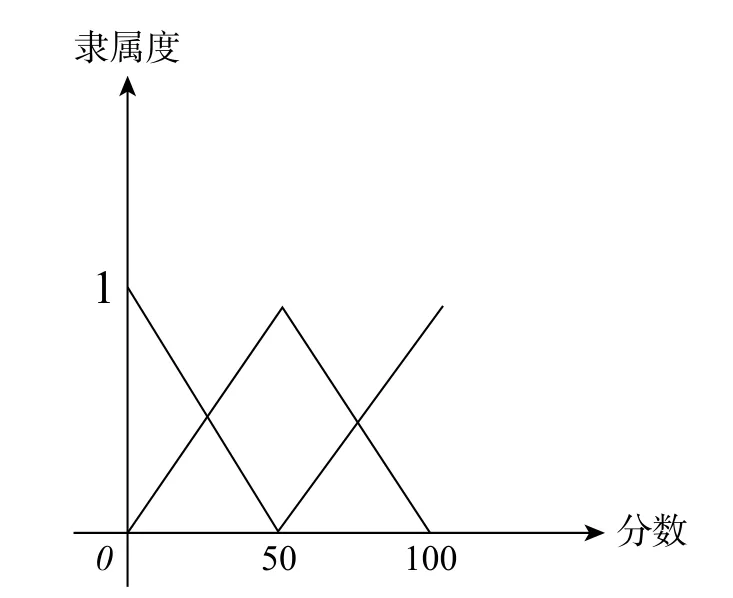
图1 身高隶属度函数图像

2.2 公理化模糊集的距离

在经典TOPSIS 方法中，我们通过计算各个备选方案与正负理想方案之间的距离来度量各个方案的优劣性。经典TOPSIS 方法的属性值在为确定的实数的情况下，计算两个方案同一属性的差异时，可以直接通过实数的运算来实现，最后使用Euclidean 距离来度量两个方案之间的距离。在本文中，我们使用自然语言所对应的公理化模糊集来对方案的不同属性进行表示并且计算，公理化模糊集在严格的公理定义下的隶属度函数为连续的函数。根据经典TOPSIS 方法的启发，我们根据扩张原理[19]来对模糊集定义四则运算及开方运算法则，将方案看作一个分量为属性值的向量，计算向量之间的距离为一个模糊集。本文对模糊集进行实数化再进行距离的比较。

定义5设V=[c,d]⊂R。定义A,B之间的四则运算结果如下所示：

定义7设两个不同向量ai,ak有m个分量，并且向量的分量由公理化模糊集表示，其中ai表 示为(ri,1,ri,2,···,ri,m)，ak表示为(rk,1,rk,2,···,rk,m)。且第j个向量的权重为wj，满足定义向量ai,ak的Euclidean 距离d(ai,aj)为

zi,j表示经过标准化处理后的分量值，zi,j的论域为[0,1]。表示用定义5 和定义6 运算规则计算出的两个向量的Euclidean 距离。

3 基于公理化模糊集合的模糊多属性决策方法

3.1 问题描述

多属性决策问题考虑从一组已知备选方案A=(a1,a2,···,an)中选出最佳方案，并且属性集C=(c1,c2,···,cm)，W=(w1,w2,···,wm)是这些属性的权重向量。在决策过程中，用定性的语言来对属性进行评价。例如从一些备选电脑中去选购一台电脑，我们这个时候可以把电脑价格的区间作为论域U，给U上一个模糊划分得到

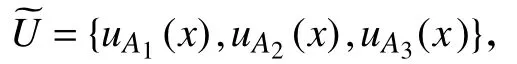
分别代表“便宜”，“中等”，“昂贵”这3 个基本评价语言值所对应的模糊集合的隶属度函数，电脑价格论域的所有模糊集都可以由上述3 个基本模糊集生成，则我们可以用公理化模糊集对应的自然语言来定性评价备选电脑。

我们可以用如下的矩阵来表示待解决的模糊多属性决策问题：

ci,j代表第i个方案第j个属性，其中的属性值是用语言值来表示的。在后续的计算中我们需要将自然语言转化为对应的公理化模糊集来建模计算。

3.2 决策方法

下面建立属性权重为实数，属性值为自然语言情况下的TOPSIS 决策模型。

第1 步,首先根据评价建立决策矩阵

其中ri,j代表第i个方案第j个属性的评价自然语言对应的公理化模糊集，属性的权重满足用表示ri,j的隶属度函数。矩阵中的模糊集隶属度函数由基本模糊集使用固定的连续三角模算子来得到。

第2 步,确定正理想方案X+和负理想方案X−：

对于多属性决策问题中的指标属性，分为两类，一类是效益型指标，一类是成本型指标。对于效益性指标，它越大越好，而对于成本性指标，则越小越好。

我们令成本型指标属性的下标集为N1，效益型指标属性的下标为N2。我们在2.1 节中讨论过有关于公理化模糊集的序关系。

对于效益型指标ri,j(j∈N2)，我们在取正理想解的时候，考虑备选方案中使这个效益型指标取最大的模糊集，对于成本性指标ri,j(j∈N1)则正好相反，取成本性指标的最小值，

则

类似对于负理想解有：

通过上述方法，我们确定了正负理想解。

第3 步,计算各个备选方案与正负理想解之间的距离，根据经典TOPSIS 方法步骤，为了消除量纲对距离的影响，首先对原始决策矩阵的属性集进行标准化处理：

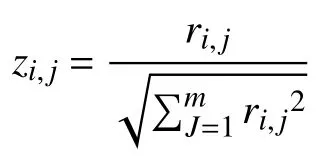
得到以下标准化决策矩阵

对正负理想解也进行标准化处理。将两个方案看作两个向量，属性值的权重为分量的权重。按照第2.2 节中的步骤得到第i(i=1,2,3,···,n)个方案与正理想解的实数距离为：

与负理想解的实数距离为

第4 步,计算每个方案到正理想方案的相对贴近度

第5 步，按照Di值从大到小对方案进行优劣排序。

4 算例分析

4.1 实例计算

选用文献[20]中实例说明上述提出方法的过程与合理性。考虑某个风险投资公司进行项目投资的决策问题。某风险投资公司在对备选企业a1～a5进行选择时，首先制定了4 项评价属性c1～c4(属性分别为风险因素、成长因素、社会政治影响因素和环境影响因素)，设这四个因素的的分数得分范围为0 到100 分。案例中没有给出属性权重的数值，我们暂时认为它所有的权重相同，都为0.25。对于4 个因素的论域都为[0,100]，我们给出相同的模糊划分为{非常差，差，中等，好，非常好}，并且给出相应的隶属度函数如图2 所示。

图2 分数隶属度函数图像

专家组评测得到备选企业的自然语言评价结果如表1 所示。

表1 语言评价结果

步骤1,建立决策矩阵

步骤2,确定正理想方案X+和负理想方案X−：

X+={非常好，非常好，非常好，非常好},

X−={差，非常差，非常差，非常差}。

步骤3,计算各个方案到正负理想方案的距离：

步骤4,计算各个方案的综合指数：

根据Di值的大小对备选企业进行排序，排序结果为：a4≻a3≻a5≻a1≻a2，可见企业4 为最优选择。

4.2 比较分析

文献[20]中选择使用三参数区间数来对属性进行分，打分结果如下所示：

专家对备选企业的影响因素进行打分时，因为人类自身判断的模糊性，选择使用自然语言，上述将专家的评价自然语言量化为区间数来进行处理，没有解释清楚区间数如此取值的合理性，并且没有从全局的角度来约束区间数的取值，造成很大的客观性。如同使用Zadeh 意义下的模糊集与Zadeh意义扩展下的模糊集相同，隶属度的确定存在较大主观性。

基于公理化模糊集的多属性决策方法中，将专家评价自然语言量化为公理化模糊集合来处理，在确定公理化模糊集合的隶属度函数过程中，从全局的角度通过模糊划分来生成基本的公理化模糊集，并且此论域的所有模糊集只能通过这组基本公理化模糊集使用特定的方式来生成，隶属度函数满足严格的公理化定义，较传统模糊集合隶属度函数的确定更加准确。本文结果与文献[20]比较如表2所示。

表2 结果比较

通过观察得知，在计算得到的结果中，文献[20]的结果为a4≻a5≻a3≻a1≻a2，而本文的结果为a4≻a3≻a5≻a1≻a2，其中结果a5与a3的结果与本文不同，a3优于a5，通过观察，方案的4 个属性值的权重一致，a3的属性评价集为（非常好，好，差，好），而a5的属性评价集为（差，中等，中等，非常好），通过直观上的对比，a3的属性中两个好优于优于a5，a3明显优于a5，验证了本文方法的准确性。其中5 个备选公司中计算出的结果最差为a2，通过直接观察a2的评价为（好，非常差，非常差，差），较其它备选公司具有明显劣势，通过上面表格中数据对比，可以看出本文方法所计算出的结果中，a2的值明显小于其它4 个备选公司的值，而文献[20]的结果中区分没有特别明显，本文的方法对更差的备选方案具有更好的区分性，决策结果更加符合我们想要的预期决策结果。通过比较分析，验证了本文决策模型的有效性与准确性。

5 结束语

本文在多属性决策过程中的属性集用自然语言表示的情况下，通过模糊划分来建立自然语言与公理化模糊集之间的对应关系，将各个属性直接表示为自然语言所对应的公理化模糊集来进行建模计算，模糊集隶属度函数满足严格公理化定义并且是连续的。很好的将自然语言量化为对应的模糊集隶属度函数。在后面计算同一属性的排序，方案之间的距离时直接使用公理化模糊集来进行计算。较以往模糊多属性决策中使用单个隶属度表示属性或者直接使用自然语言没有对应的隶属度函数来表示属性更加准确，客观。本文没有考虑权重信息为模糊的情况下，在未来，可以考虑以公理化模糊集合为基础，并且权重、属性都为模糊情况下的多属性决策方法。