基于距离测度的三角模糊交互多属性决策方法

李 霞，张绍林，逄格炜

（1.青岛农业大学档案馆,山东 青岛 266109；2.中南大学商学院,湖南 长沙 410083；3.青岛农业大学动漫与传媒学院,山东 青岛 266109）

模糊多属性决策能够有效刻画人们面对复杂决策问题时主观认知的不确定性，在实际生产、生活中有着广泛的应用，并相继出现多种模糊变量类型。自VAN LAARHOVEN 等[1]首次使用三角模糊数表示模糊评价信息以来，国内外学者关于三角模糊多属性决策问题进行了大量的研究，现阶段已取得丰富的学术成果。例如，付沙等[2]针对属性权重和决策矩阵均为三角模糊数的多属性决策问题，提出了一种基于集对分析的多属性决策方法。针对动态三角模糊多属性决策问题，梅晓玲[3]以各时段属性值与对应三角模糊属性值均值水平的离差为研究对象，通过构建效用函数模型将离差值转化为精确效用函数值，并由此得到方案排序。赵萌等[4]将策略权重操控问题的研究拓展到模糊多属性决策，提出了基于可能度和贴近度公式的混合线性规划模型来得出排名范围，并建立决策者策略权重向量最优模型。此外，WANG 等[5]给出综合模糊层次分析法和模糊VIKOR 法的混合多属性决策方法来解决可持续供应链第三方物流供应商选择问题。经文献梳理发现，关于三角模糊多属性决策问题的研究还存在一定局限性，如现有排序方法无法确定两个不同三角模糊数的大小关系，已有三角模糊多属性决策方法的研究主要是基于属性相互独立的前提下展开的，通常情况下，决策属性指标体系应具有独立性，但在实际问题中，属性指标间的独立性常常难以满足。例如，若用价格、性能和售后3 个属性指标选择设备，一般来说，性能和售后好的设备价格高，这种属性间存在的交互作用使得属性权重不满足可加性[6]。因此，本文对属性间存在交互作用的三角模糊多属性决策问题进一步展开研究。

1 预备知识

这里首先介绍一下关于三角模糊数及可信性分布的基本知识，以便进行后续探讨。

定义1[1]定义在实数域 R上的模糊数=(aL,aM,aU),其中aL≤aM≤aU，称为三角模糊数，其隶属函数µa˜:R →[0,1]表示为：

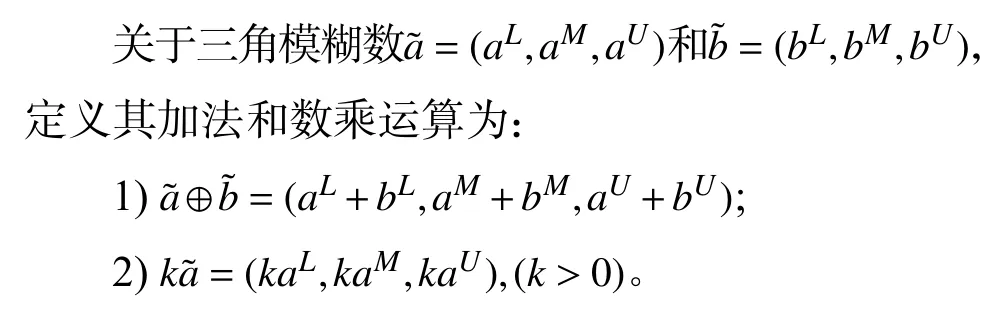
定义2[7]设 Θ是一个非空集合，P(Θ)为 Θ的幂集。Cr是定义在P(Θ)上的集函数。若Cr满足以下四条公理，则称Cr是一个可信性测度。

公理1（规范性）Cr{Θ}=1。

公理2（单调性）如果A⊆B，则有Cr{A}≤Cr{B}。

公理3（自对偶性）对于任意A∈P(Θ)，Cr{A}+Cr{AC}=1。

三元组(Θ,P(Θ),Cr)称为可信性空间。

定义3[8]一个模糊变量就是指从可信性空间(Θ,P(Θ),Cr)到实数集上的函数。

定义4[9]对于一个模糊变量ξ，其可信性分布Ψ :R →[0,1]定义为

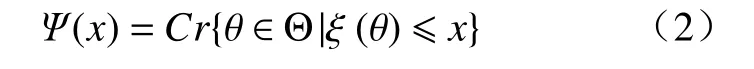
也就是说，可信性分布Ψ(x)反映的是模糊变量ξ取值小于或等于x的可信度。结合三角模糊数=(aL,aM,aU)隶属函数表达式,我们可以得到其可信性分布

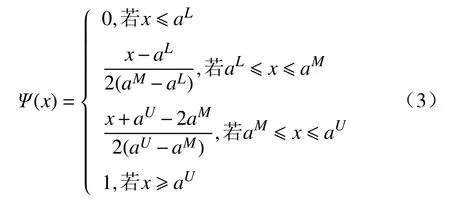
相应的直观表示，如图1 所示。

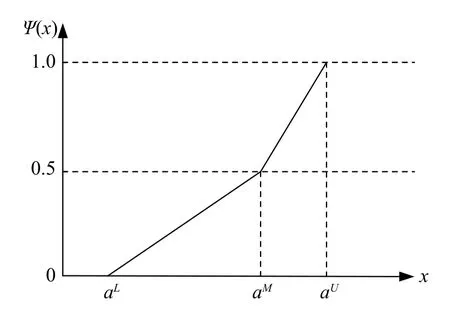
图1 三角模糊数的可信性分布

2 三角模糊数的排序方法

甘庭聪等[12]利用可能度研究三角模糊数的排序方法，根据不同情况，分别给出了相应的可能度计算公式。对于三角模糊数=(0.1,0.4,0.5)和=(0.2,0.3,0.5)，按照文中的分类规则，应采用的可能度公式为

针对上述一些排序方法的局限性，这里结合可信性分布理论给出新的排序方法。

期望值反映了模糊数的中心趋向，通常用来表示模糊数的大小。基于前面关于三角模糊数的可信性分布，LIU 等[7]给出了三角模糊数a˜的期望值直观上看，图1 所示的可信性分布面积反映了三角模糊数的不确定性，当面积为0 时，三角模糊数退化为实数。对于三角模糊数容易得到其可信性分布的面积

按照本文的三角模糊数排序方法可以有效解决现有方法无法区分不同三角模糊数大小的问题。

证明充分性显然成立。现证必要性，若，由以上比较规则，我们有

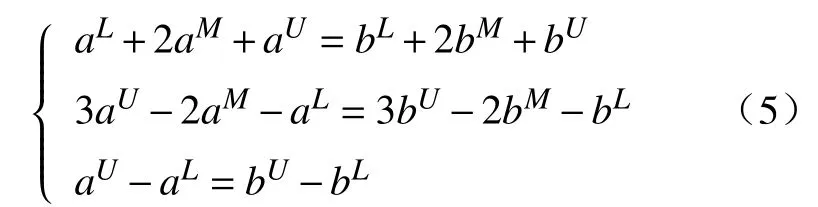
求解方程组，可得aL=bL，aM=bM，aU=bU。定理得证。

3 三角模糊数的距离测度

对于区间数IRPINO等[13]基于一维均匀分布视角，给出了以下距离公式：

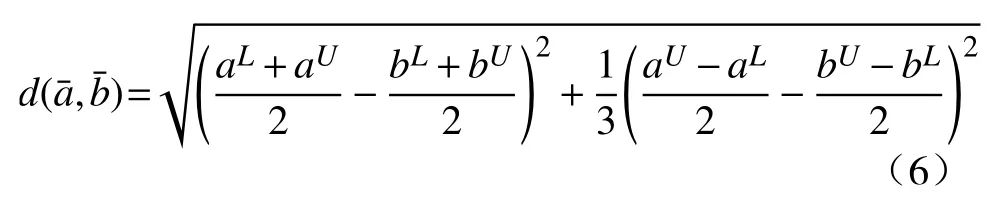
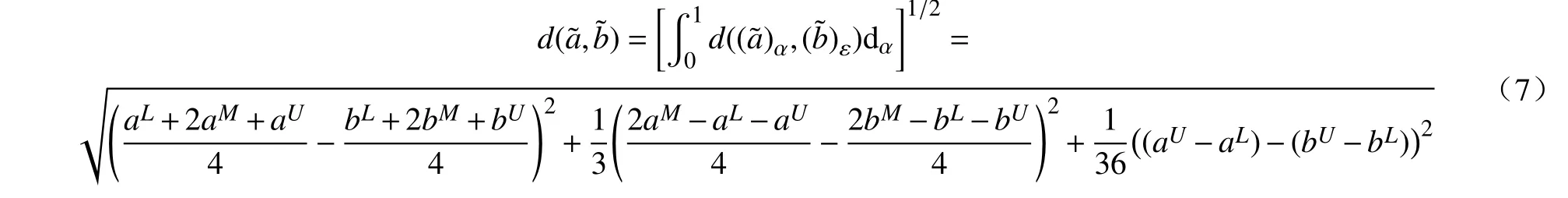
4 考虑交互作用的模糊多属性决策方法

4.1 基于Shapley 指数和2-可加测度的三角模糊信息集结算子

传统的多属性决策方法中的信息集结往往建立在属性相互独立、互不影响的假设前提之上，而现实问题中的多个决策属性间往往是相互关联的。为了应对属性之间的交互作用现象，SUGENO[14]提出了模糊测度的概念。

定义5[14]有限集合N={1,2,···,n}上的一个模糊测度µ:P(N)→[0,1]满足：

1)µ(φ)=0,µ(N)=1；

2)若A,B∈P(N)且A⊆B，则µ(A)≤µ(B)。

其中P(N)是N的幂集。

基于可加测度的集结算子不再适于模糊测度的情形，因此，可以采用Choquet 积分进行信息集结。

定义6[15]f是定义在X={x1,x2,···,xn}上的非负实值函数，µ是N上的一个模糊测度，函数f关于µ的Choquet 积分定义为：

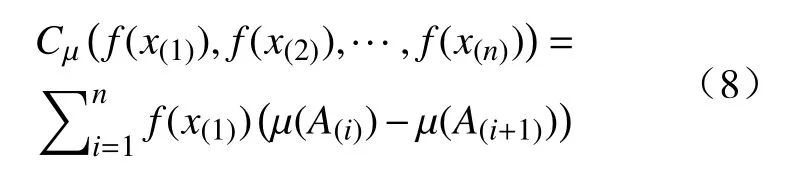
其中 (·)表示X中元素下标的一个置换，使得f(x(1))≤f(x(2))≤···≤f(x(n)),且A(i)={x(i),x(i+1),···,x(n)}，A(n+1)=φ。

由定义5 可知，模糊测度定义在集合的幂集上，当决策属性数量为n个时，需要确定 2n个参数，这种复杂性限制了其实际应用。为此，文献[16]提出了k-可加模糊测度，随着k的增加，模糊测度的参数也越多，其表现能力就越强，而2-可加测度只涉及到属性的相对重要性和2 个属性间交互性，较好解决了复杂性和表现能力之间的矛盾，在实际应用中得到了认可[17]。因此，我们进一步采用2-可加测度来代替一般的模糊测度。

定理2[16]设 µ为N={1,2,···,n}上的一个模糊测度,则 µ为一个2-可加测度，当且仅当对所有的i,j∈N，都存在 µ(i) 和 µ(i,j)满足以下条件:

1)µ(i)≥0(∀i∈N),

2)∑{i,j}⊆Nµ(i,j)−(|N|−2)∑i∈Nµ(i)=1,

3)∑i∈Sj(µ(i,j)−µ(i))≥(|S|−2)µ(j)(∀S⊆N),其中j∈S且|S|≥2。

Shapley 函数是合作博弈论中一个重要的分配指标，根据各参与者对其所参与联盟的边际贡献的期望值来确定最优收益分配方案。而在实际多属性决策问题中，也存在属性间相互关联、相互依赖的现象。因此，文献[18]将Shapley 函数引入到模糊测度中，用来反映多属性决策问题的属性权重。为方便使用，MENG 等[19]给出了如下关于2-可加测度的Shapley 指数表达式：

基于以上分析，我们给出如下2 可加Shapley三角模糊Choquet 积分集结(2ASTFCA)算子：

容易验证，该算子满足幂等、有界及单调性。

4.2 求解最优2-可加测度的规划模型

对于一个三角模糊多属性决策问题，令方案集A={a1,a2,···,am}，属性集C={c1,c2,···,cn}。方案ai在属性cj下的属性值为定义在[0,1]上的三角模糊数即相应的决策矩阵记为R=当属性权重完全已知时，可以利用集结算子求得方案综合属性值，而更多的情形是，只有关于属性的部分权重信息，记为Wj(j=1,2,···,n)。

在多属性决策中，方案之间的离差越大就越容易区分方案优劣关系。为得到属性权重，需要先求得各属性的2-可加测度。为此，基于前面定义的三角模糊数距离测度，我们以各个方案之间离差最大化为目标，构建规划模型(M-1)：

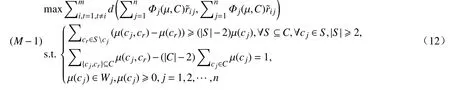
其中，Φj(µ,C)为属性cj的Shapley 值，µ为定义在属性集C上的2-可加测度，d为三角模糊数之间的距离测度，Wj为属性cj的部分权重信息。

通过求解模型(M-1)，可以得到关于属性集的最优2-可加测度，然后由式(9)求得各属性的Shapley 值并作为属性权重。

4.3 决策步骤

基于上述分析，我们给出以下决策步骤。

第3 步：通过模型(M-1)确定属性集C上的2-可加测度。

第4 步：由公式(9)计算各属性cj的Shapley 值。

第5 步：应用2ASTFCA 算子得到各方案ai的综合三角模糊评价值。

第6 步：采用本文给出的三角模糊数排序规则进行方案排序。

5 算例分析

作为深度开发农业资源潜力、增加农民收入的一种创新途径，休闲农业近年来已经进入一个全面发展的时期。青岛市作为传统旅游城市，将休闲农业作为农业转型升级突破口，取得了显著的成效。已初步构建起“食、住、行、游、购、娱”为一体的休闲农业格局。但由于休闲农业项目呈个体小型化和区域分散性特点，存在着休闲农业旅游信息获取难、不准确、无法满足个性化需求，高峰时期不能提供导流分流及缺少及时有效的问题反馈机制等问题，极大地影响了游客旅游体验，并在一定程度上制约了青岛休闲农业的产业化发展。随着第五代移动通讯(5G)及物联网等现代信息技术的飞速发展，通过构建青岛市休闲农业综合信息服务平台能够有效解决上述问题。目前市场上能够提供该平台开发的软件开发方较多，经过初步筛选，得到了4 家开发方以做进一步评价，记为A={a1,a2,a3,a4}。关于休闲农业综合信息服务平台的评价主要围绕安全稳定性、功能完备性、兼容性、可维护性、经济性5 个属性，记为C={c1,c2,c3,c4,c5}，各属性的重要性范围为：W1=[0.2,0.25]，W2=[0.15,0.25]，W3=[0.15,0.2]，W4=[0.2,0.3]，W5=[0.1,0.2]。决策者以[0,1]上的三角模糊数对方案在各属性下进行评价，并得到如下决策矩阵

由于所有属性均为效益型，无需进行规范化处理。由模型(M-1)，可得到：

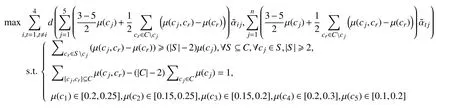
利用Lingo 软件求解该模型，可得到属性集上的最优2-可加测度：

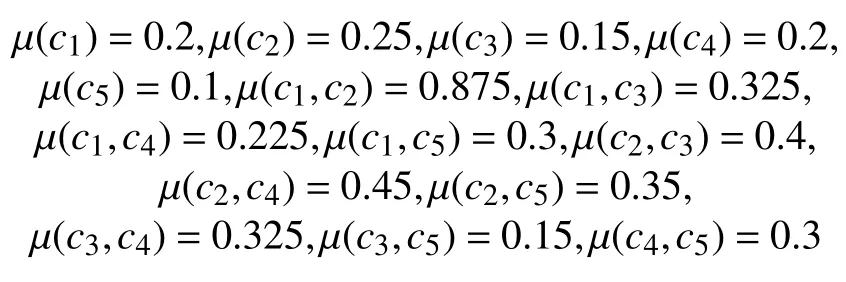
再由公式(9)求得各属性的Shapley 值：

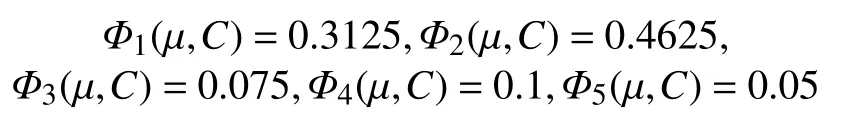
然后通过2ASTFCA 算子集结得到各方案的综合属性值：

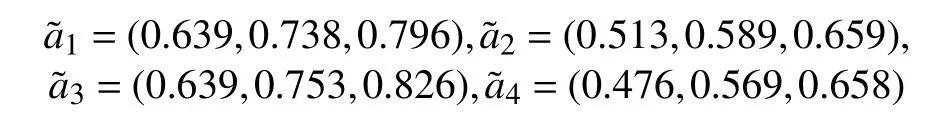
最后按照本文给出的三角模糊数排序方法，可得到4 个方案的排序结果为：a3≻a1≻a2≻a4。

6 结束语

为确保三角模糊多属性决策问题能够得到更准确的决策结果，本文基于可信性分布理论提供了一种关于三角模糊数的新排序方法。通过扩展区间数的Wasserstein 距离，给出了三角模糊数的距离公式。针对属性间的交互作用，定义了基于2-可加测度和Shapley 指数的集结算子对三角模糊决策信息进行集结，并给出在部分权重信息下通过构建规划模型求解最优2-可加测度的方法。最后，结合青岛市休闲农业综合信息服务平台开发方选择问题，说明了所给方法的求解过程及有效性。