离心泵部分负载下进口二次回流成因分析及验证
王 桃,周星丞,周 敏,向 茹
(1.流体及动力机械教育部重点实验室(西华大学),四川 成都 610039;2.西华大学能源与动力工程学院,四川 成都 610039)
离心泵在小流量下运行时,叶轮入口会出现回流[1−2]。回流是指部分已进入叶轮流体又在大半径处返回叶轮入口,然后随同主流第二次进入叶轮的现象[3]。国内外的许多学者对离心泵进口回流进行过研究。侯敬生[4]发现回流发生时,会导致叶轮进口轴线附近的压力降低,进口回流影响范围随流量减小而扩大,进一步恶化叶轮进口的流动。回流产生的原因作者归纳为部分负载时部分流体质点在离心力作用下撞向固体壁面造成该区域的速度和压力变化而形成的。林刚等[5]以一低比转速离心泵为研究对象,采用数值计算方法分析了叶轮几何参数对离心泵进口回流特性的影响,得到了叶片数、叶片进口冲角和叶片进口边位置3 个叶轮几何参数对进口回流强度的影响规律。
目前,国内外学者对回流现象、回流对离心泵外特性的影响以及如何减小回流对泵性能的影响研究较多,但对回流成因的探讨涉及不多,还没有取得普遍认可的解释[6−9]。认识回流的现象及原因是一项基础性工作,对全面了解离心泵的流动机理有重要意义。
本文将从理论上分析强制涡压力分布规律,阐明离心泵部分负载下压力分布特点,进而从理论上探讨进口二次回流产生的原因,采用数值计算分析泵在部分负载下叶轮进口附近压力及流场分布规律,结合泵叶片进口切割实验对比分析二次回流对泵外特性的影响,有助于同行对泵的流动特征有更深入的认识与了解。
1 二次回流产生的机理分析
1.1 强制涡压力分布特点
强制涡是指像刚体一样绕一垂直于流动所在平面的轴心线以不变的角速度旋转的水体,强制涡的流体质点的速度方向与流体轨迹圆相切,速度大小正比于质点到轴心线的半径。
在一单位厚度的强制涡中,取一半径为R和R+dR的扇形水体,扇形两腰夹角为dφ。由于流动的对称性,在同一半径上流体压力为常数,小半径和大半径上压力分别为P和P+dP,压力以向心方向为正值,如图1 所示。
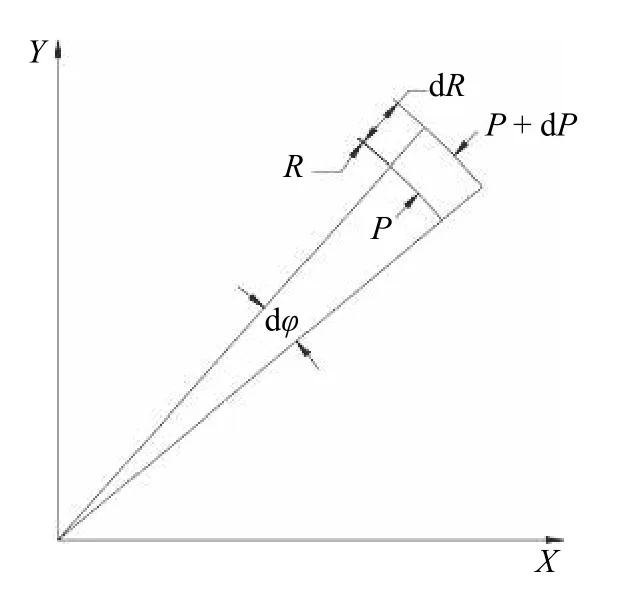
图1 扇形水体
小圆弧上总压力为PRdφ(Rdφ为面积),这一值向外为负值。大圆弧上总压力为

这一压力向内为正值。扇形水体两个侧面压力为2PdR,其径向分量为
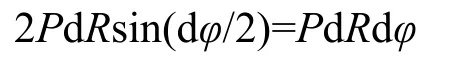
当dφ很小时,上式中sin(dφ/2)=dφ/2,这一分量向外取负值,水所受到的径向方向的合力为

推导中略去了高阶项dPdRdφ。
设扇形水体在小半径的各点圆周速度为Vu,那么水体向心加速度为,水体质量为ρRdRdφ。由于水体所受外力是水体产生向心加速度的原因,从而有,即

对于强制涡,前面所述有Vu=Rω,ω为水体绕轴心线旋转角速度。将这一关系代入式(3),得到dP/dR=ρRω2,积分上式有:
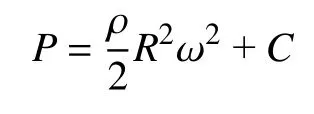
设强制涡中心压力P0,可得到C=P0,由此可获得以下强制涡中压力随半径的变化规律。
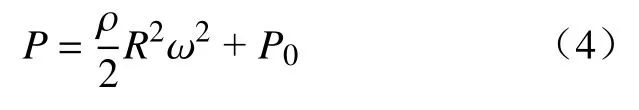
即强制涡中压力随半径增大按抛物线规律上升。
1.2 入口二次回流产生原因
在水泵出口阀门关闭且叶轮旋转时,运动叶片会因为水的粘性带动叶片附近的水开始运动,并逐渐加快速度,这层水又会因黏性的作用带动下一层水旋转。经过充分长的时间后,各层旋转水体的旋转速度趋于一致,由此黏性水流将在叶轮入口附近生成一轴心线与叶轮轴心线重合的强制涡,强制涡的旋转角速度等于叶轮旋转角速度。这一强制涡出现在叶轮入口稍前,直到叶轮足够远的上游处这一强制涡的影响才会消失。Peclc 和Shwtiger 曾做过引起业内普遍重视的实验以研究离心泵叶轮在出口阀门关死条件的进口流态,根据实验结果绘制的叶轮入口流线如图2 所示[10]。由图2 中可以清楚地看到叶轮入口典型二次回流的流动特征。水总是从高能量处流向低能量处,或者说沿负压梯度的方向流动。在图2 中,在叶轮入口大半径处,水流向管路上游逆向流动,表明在大半径处叶轮入口的B区域压力大于上游不受叶轮旋转影响的A区域内的压力;相反,在入口管道小半径处水流从上游正向流向叶轮入口,表明小半径处B 处压力小于A处静止水体压力。从上述不同点处压力大小的比较中可以看到,在叶轮入口处垂直于叶轮轴心线的截面上,从管心到管壁压力是逐步增大的,这一压力分布呈轴对称,且与强制涡中压力表达式(4)所给定的压力随半径变化规律一致。当然,自由涡中压力分布也有这样的定性特点,但在零流量下旋转叶轮入口显然不具备生成自由涡的条件。图2 所示实验结果实际上暗示在叶轮零流量下,在距叶轮入口不远的垂直于叶轮轴心线上出现了一强制涡。

图2 叶轮入口回流[10]
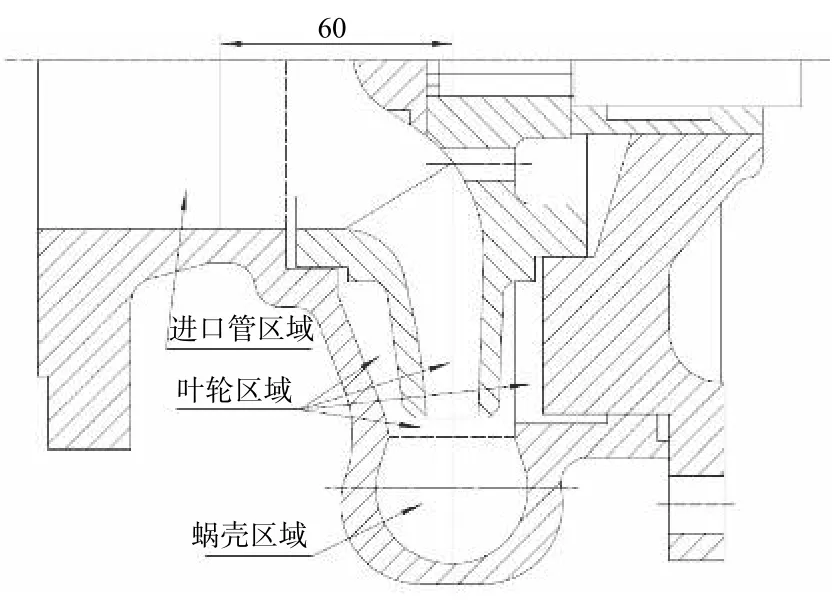
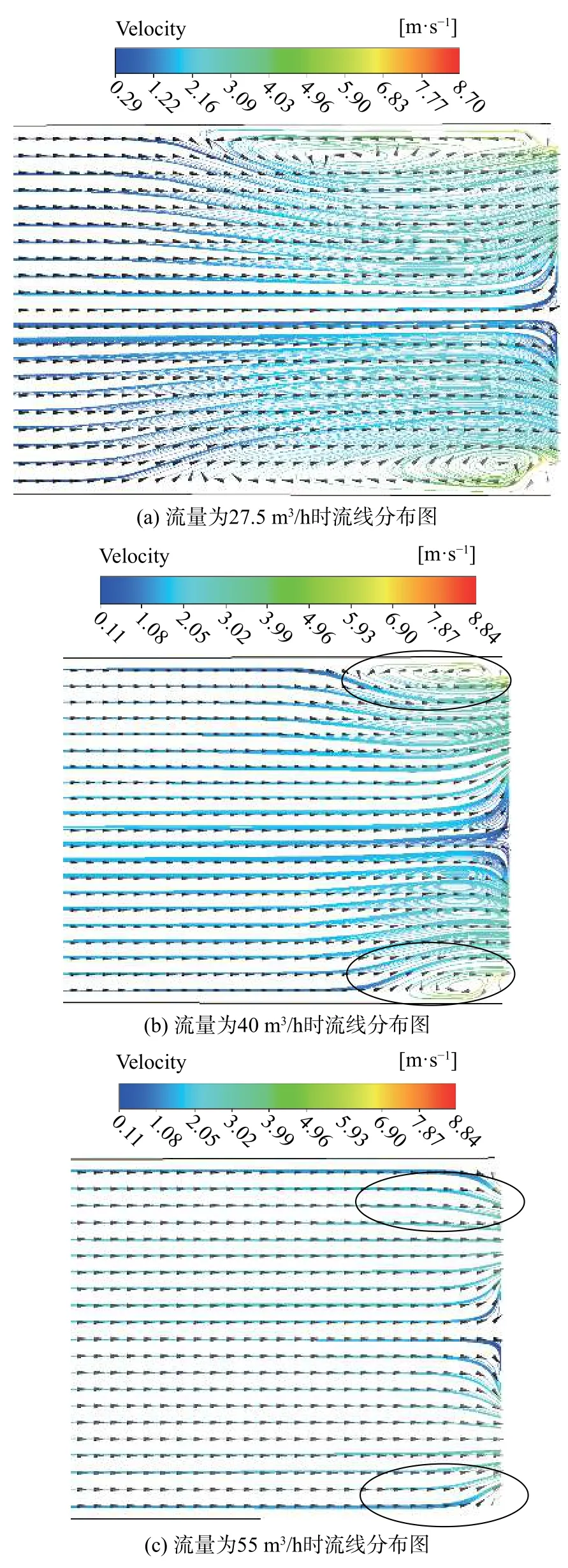
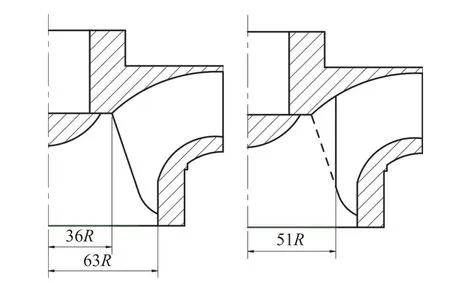
图3 为AB区域的压力分布图。图中Rs表示进口管道内径。在大半径处即图3的Rc到Rs区间,水由B区域流向A区域,在半径Ra(Rc 图3 AB 区域的压力图 将泵出口阀门开启后,通过泵的流量为QP。由这一流量引起的进口管平均速度为这时大半径处,背离叶轮的回流速度被Cd所抵消,回流速度减小。当泵出口阀门继续开大,QP及Cd将继续增大,最后回流现象消失。 为验证在部分负载时泵入口的形态,选取一比转速为66的泵为研究对象进行数值计算。泵的几何特征参数如表1 所示。 表1 泵的主要几何参数 为提高数值模拟准确性,建立了包括进口管、叶轮、蜗壳、前泵腔和后泵腔5 部分在内的全流道计算域三维模型,考虑进出口流态对计算收敛性和准确性的影响,在进口管段和蜗壳出水段分别作了一定延伸。网格划分质量对计算收敛性与计算速度均有重要影响。本文采用六面体结构化网格对计算域进行网格划分,同时对壁面进行了边界层划分。图4为计算域网格。 图4 计算域网格 本文对网格无关性进行了研究,当网格数在110 万以上时,泵扬程和效率偏差均在0.5%以内,因此本文用于计算的网格总数为1 128 804。 本文基于ANSYS CFX 平台对泵的内部流动进行稳态分析,采用k-ε湍流模型,输送介质为25 ℃清水,参考压力设为1 个大气压,近壁区应用标准壁面函数,固壁面采用无滑移边界条件,动静交接面设置为Frozen Rotor 模式,叶轮的旋转速度设为1 500 r/min,过流表面粗糙度设置为50 μm,计算收敛精度为0.000 001。设置静压进口,质量流量出口的边界条件,通过调节出口的流量,模拟得到泵在不同工况运行时的性能。 在江苏大学流体机械质量技术检验中心精度等级为一级的一泵开式实验台进行泵外特性测试,将试验数据与数值模拟结果进行对比,结果如图5所示,表2 列出了泵高效点性能参数。 图5 泵性能数值模拟与实验结果对比 表2 泵高效点特性参数 由图5 和表2 可以看出,数值计算得到的特性曲线与实验获得的曲线变化趋势吻合,数值计算的效率高于试验值,虽然与试验值有一定差异,但两者的趋势一致,计算与试验效率差值的变动范围较小,数值计算结果相对稳定。因此,本文采用的数值计算方案可以对泵性能进行较为准确的模拟。 本节将重点讨论在部分负载时泵进口管内的压力及速度分布。为便于问题讨论,在距叶轮中心60 mm 处取一与叶轮轴心线相垂直的平面与进水管相交,该径向截面位置示意图如图6 所示。 图6 进口管内径向截面位置示意图 图7 为27.5 m3/h 流量时进水管径向截面内速度矢量分布图。图中可以看到靠近管壁处速度高,从管壁向管中心方向速度基本按线性规律减小。这一现象与强制涡速度分布规律一致,说明在小流量工作条件下,叶轮入口稍前的区域出现了一个强制涡。 图7 流量为27.5 m3/h 时进口管径向截面内速度矢量分布图 图8(a)为流量27.5 m3/h 时进口管径向截面内压力分布图,图8(b)为相同流量时进口管轴向截面内压力分布图。当泵运行在部分工况时,从叶轮入口附近进口管径向截面压力分布云图8(a)中可以看出,管路径向截面内压力呈轴对称,压力在管壁处最高,且向中心方向逐渐减小,这一压力随半径变化的规律与前文分析的强制涡中压力分布规律一致。图8(b)进一步证实了上述部分负荷条件下叶轮入口压力分布规律,同时该图还表明,在距叶轮有一定距离的不受叶轮旋转影响的上游处,在不同半径上压力并无变化,结果在不同半径上,上游压力可能大于或小于叶轮入口压力。这种压力差形成了不同半径上的流体流向不同,这是产生叶轮入口二次回流的原因。 图8 流量为27.5 m3/h 时进口管压力分布图 图9(a)为流量27.5 m3/h 时,进口管轴向截面内流线分布图。可以看出在此部分工况下进口管内存在明显的二次回流区。当流量增大到40 m3/h 时,如图9(b)所示,进口管内主流速度提高,回流速度被抵消,同时回流影响区也明显缩小。当泵进口流量增大到设计流量55 m3/h 时,进口管内主流平均速度将完全抵消回流速度,回流现象消失。图9(c)为泵在高效点(流量55 m3/h)时进水管轴向截面内流线分布图,从图中看到进口管内的回流现象已完全消失。 图9 不同流量时进口管轴向截面内流线分布图 设通过泵的主流流量为QP,通过叶轮获得扬程HP,设回流流量为QR,回流流量第一次通过叶轮获得的扬程HR,第二次穿过叶轮获得的扬程为HP。由于二次回流的回流量两次通过叶轮,从叶轮中第二次获得能量,回流流量两次获得的总扬程为HR+HP,当其汇入主流后,将提高泵的总扬程。设泵的平均扬程为H,有 从而 式(5)表明H是QR增函数,回流流量QR越大,泵的平均扬程H就越高。这一结论已为实验所证实。 文献[10]介绍了一个实验结果。在一闭式试验台上,对两个具有不同叶片进口几何特征的叶轮进行了外特性实验,实验叶轮如图10 所示,在图10的右图中,虚线为原叶片,实线为切割后的新叶片。实验结果如图11 所示,新叶片的旋转水体对叶轮入口影响减小,叶轮二次回流被抑制。在小流量区域叶片切割后因叶轮入口二次回流被抑制,叶片产生的扬程较原型叶轮低,见虚线(II)。而未切割的叶片,由于叶轮入口有二次回流,会造成小流量下扬程提高,见实线(Ⅰ)。同时,叶片入口切割对泵的效率影响不大,见图11 下方的曲线。由此可见,原型叶轮入口有二次回流时,能够在一定程度提高泵在小流量区域的扬程,对消除H-Q曲线的驼峰有一定的积极作用。 图10 叶片进口切割前后的实验叶轮示意图 图11 流量扬程与流量效率曲线[10] 1)在泵出口阀门关闭时,旋转叶轮将在叶轮入口诱导产生一强制涡。强制涡中压力随半径R的变化规律为即压力随半径增大按抛物线规律上升。 2)在小流量工况下,在叶轮入口稍前的管道径向截面内,由于叶轮的旋转作用和流体黏性将产生一强制涡。强制涡内的压力将从边壁处的最大值向中心方向减小。在不同半径上,强制涡中的压力与上游未受旋转叶轮影响的区域压力不同,在此压差的作用下,不同半径上水流流向不同,由此形成了叶轮入口的二次回流。随着叶轮流量增大,入口处的主流将抵消二次流效应,二次流随流量增大而逐步消失。 3)叶轮入口二次回流将提升叶轮的扬程,对消除泵的H-Q曲线的驼峰也有一定的作用,是一种积极的现象。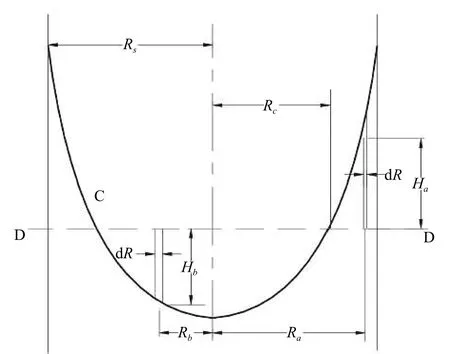
2 数值计算验证

2.1 几何造型及网格划分
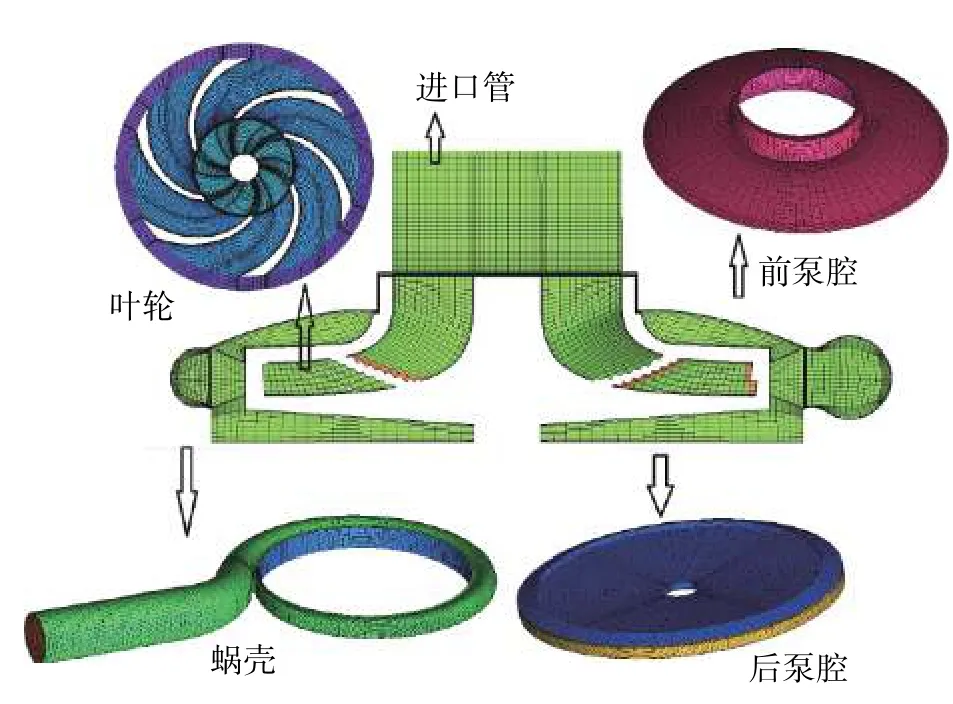
2.2 CFX 求解设置
2.3 数值计算与实验验证对比
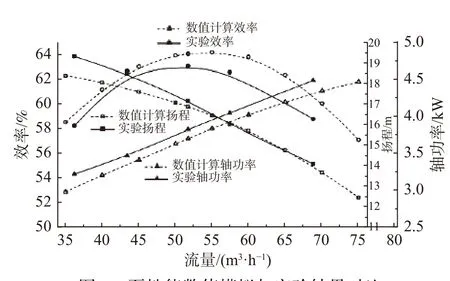
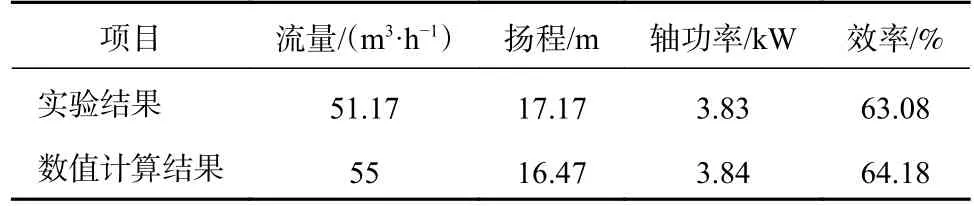
2.4 内流场分析


3 叶轮入口回流对泵外特性的影响



4 结论

