基于组合赋权的直觉模糊多属性动态决策方法
周雨婷,叶国菊*,刘 尉,赵大方,李 宁
(1.河海大学理学院,江苏 南京 210098;2.湖北师范大学数学与统计学院,湖北 黄石 435002;3.火箭军装备部驻南京地区第二军事代表室,江苏 南京 210006)
模糊集自1965 年被Zadeh[1]提出后,模糊理论已在工程、技术、管理等各个领域得到广泛应用。1986 年保加利亚学者Atanassov[2−3]对Zadeh的模糊集进行了拓展,提出了直觉模糊集的概念。由于直觉模糊集同时考虑了隶属度、非隶属度和犹豫度3 个方面的信息,因此它比传统模糊集在处理模糊性和不确定性方面更具灵活性和实用性,也因此被广泛地应用到决策领域,并取得了丰硕的研究成果。2005 年Li[4]研究了属性权重和属性值均为直觉模糊数的多属性决策问题,并提出了一种基于线性规划模型的多属性决策方法;2007 年徐泽水[5]研究属性值为直觉模糊数且决策者对决策方案有偏好的模糊多属性决策问题,并通过建立线性规划模型来确定属性权重,进而给出了一种基于直觉模糊偏好信息的多属性决策方法;2008 年南江霞等[6]研究了属性值和权重都是直觉模糊集的多属性决策问题,并提出了一种基于TOPSIS 方法的直觉模糊多属性决策方法;2009 年卫贵武[7]和2013 年何霞等[8]研究了对方案有偏好的直觉模糊多属性决策问题;2018 年曾守桢等[9]针对属性之间具有相互关联关系的直觉模糊多属性决策问题,提出一种基于Zhenyuan 积分的决策方法;于瑞华等[10]研究了属性权重信息不完全确定,属性值为直觉模糊集的多属性决策问题,并提出一种基于意见排序法的直觉模糊多属性决策方法;2020 年刘利枚等[11]研究直觉模糊多属性群体共识决策问题,并基于直觉模糊共识模型与专家权重优化模型给出一种直觉模糊环境下的多属性群决策方法。
上述研究成果根据已知的模糊信息,从主观或者客观的角度来确定属性权重进而进行决策。然而,在实际决策过程中,考虑决策者的主观偏好和提高决策结果的科学性和客观性均是很有必要的。为此,本文在直觉模糊信息环境下,针对属性权重信息不完全确定的多属性决策问题,提出了一种新的基于离差最大化和层次分析的多属性动态权重决策方法。该方法将主观和客观两类权重信息相结合,通过组合赋权,既能充分利用客观信息,又能尽可能地满足决策者的主观意愿,并为属性权重不完全确定的直觉模糊多属性问题,提供一种新的简便易操作的决策方法。
1 预备知识
定义1[12]设X是一个非空集合,X={x1,x2,···,xn},X上的一个直觉模糊集A是具有如下形式的一个三元组:
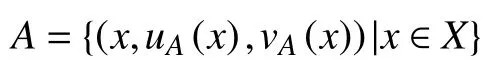
其中:uA:X→[0,1]和vA:X→[0,1]满足0 ≤uA(x)+vA(x)≤1,x∈X。函数uA(x),vA(x)分别称为x∈X关于直觉模糊集A的隶属度函数和非隶属度函数。X上所有直觉模糊集的集合记为F(X)。对于∀x∈X,称πA(x)=1−uA(x)−vA(x)为x属于直觉模糊集A的犹豫度。
定义2[12]设A∈F(X)、B∈F(X)为两个直觉模糊集,称d(A,B)为直觉模糊集A和B的加权汉明距离
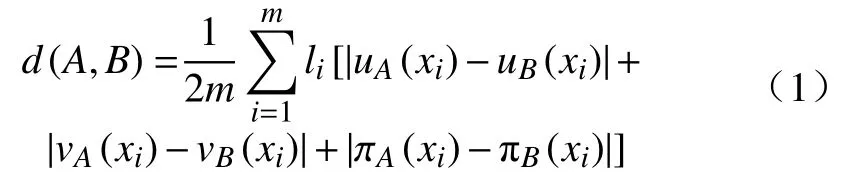
其中,l=(l1,l2,···,lm),li≥0,i=1,2,···,m,为权重。
定义3[12]设Θ ∈F(X),ai=(ui,vi),i=1,2,···,n为 Θ中的一组直觉模糊数,且设IFWA:Θn→Θ,若
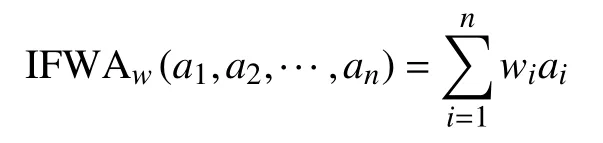
则称函数IFWA为直觉模糊加权平均算子,其中,w=(w1,w2,···,wn)为ai(i=1,2,···,n)的权重向量,wi≥0,i=1,2,···,n,
根据直觉模糊数的运算法则,可得

定义4[12]设aj=(uj,vj)(j=1,2)是两个直觉模糊数,s(a1)=u1−v1和s(a2)=u2−v2分别为a1和a2的得分值,h(a1)=u1+v1和h(a2)=u2+v2分别为a1和a2的精确度,则
若s(a1) 若s(a1)=s(a2),则 1)若h(a1)=h(a2),则a1等于a2,即a1=a2; 2)若h(a1) 3)若h(a1)>h(a2),则a1大于a2,记为a1>a2。 在一些实际决策问题中,由于受客观环境、专业水平、以及时间等诸多因素影响,决策者往往不能提供对决策方案的精确偏好信息。因此,本节从属性权重的角度出发,提出一种基于组合赋权法的多属性动态决策方法。 属性值为直觉模糊数的多属性问题,一般描述如下:有n个 备选方案和m个评价属性,记A=(A1,A2,···,An)为方案集,G=(G1,G2,···,Gm)为属性集,属性集的权重记为w=(w1,w2,···,wm)。决策者对于方案Ai关于属性Gj进行测度,得到方案Ai关于属性Gj的评价值rij=i=1,2,···,n,j=1,2,···,m,其中ui j表示决策者关于属性Gj对方案Ai的满意程度,vi j表示决策者关于属性Gj对方案Ai的不满意程度,且ui j,vij∈[0,1],0 ≤uij+vij≤1,记直觉模糊决策矩阵为 显然,综合评价值ri越大,则其所对应的方案Ai越优,在权重向量已知的情况下很容易对方案进行排序。由于客观事物的复杂性及人类思维的局限性和模糊性,人们往往难以给出明确的属性权重,这时的属性权重信息不完全。在这种情况下,需要事先确定属性的权重。下面,我们给出一种求解属性权重的方法。 1)确定客观权重。根据离差最大化的思想[13],如果属性Gj对所有决策方案而言均无差别,则属性Gj对方案决策与排序将不起作用,这样的评价属性可令其权系数为0;反之,如果属性Gj能使所有决策方案的属性值有较大差异,这样的评价属性对方案决策与排序将起重要作用,应该给予较大的权系,假设属性的客观权重为l=(l1,l2,···,lm),li≥0,且满足单位化约束条件详见文献[13]。 由于在直觉模糊决策矩阵R中 不能直接使用传统的离差最大化方法求属性的客观权重,对此,给出一种基于离差最大化确定直觉模糊属性权重的方法。 根据公式(1),对于属性Gj而言,决策方案Ai与其他方案Ak之间的加权汉明距离为 则Dj(l)表示对属性Gj而言,所有方案与其他方案的总离差。根据离差最大化的思想,属性权重l的选择应使所有属性对所有决策方案的总离差最大。因此,求解属性权重向量就等价于求解如下单目标优化模型 为求解该单目标优化模型,可构造拉格朗日函数 对其求偏导数,并令偏导数等于0,可得 解之得 对lj进行归一化处理,得属性的客观权重为 2)组合赋权。多属性决策问题中,层次分析法是对一些较为复杂模糊的问题作出决策的多准则决策分析方法,主要目标是解决多目标的复杂问题。为了得到属性的主观权重,决策者(专家)首先根据主观经验用0.1~0.9 互补标度[14]判断属性之间的相对重要程度,得到模糊互补判断矩阵 其中,bi j表示第i个属性和第j个属性比较的标度值。 目前,有关互补判断矩阵的排序理论和方法已有较多的深入研究,这里我们参考文献[15]提出的一种经典的互补判断矩阵排序方法,即 则得属性的主观权重向量为 主观法确定的属性权重体现了决策者的意向,但决策或评价结果具有较大的主观随意性;客观法所确定的属性权重虽具有较强的数学理论依据,但忽略了决策者的主观意向。为了既照顾到决策者的主观偏好,又做到决策的客观真实性,因此,本文在属性完全不完全确定的情况下,对第j个属性的主观权重和客观权重进行线性组合,得出第j个属性的动态组合权重,即: 其中 λ为调节系数,λ ∈[0,1];λ、(1−λ)分别为评价指标的主、客观权重的偏好系数;wlj,wrj分别表示第j个评价属性权重的最大值和最小值。 根据公式中的不等式组,可以确定调节系数λ的取值范围,λ越大,说明评价相对越主观,λ越小,说明评价相对越客观。 综上所述,得到了一种新的直觉模糊多属性决策方法,具体算法如下所示。 步骤1:对于某一多属性决策问题,获取方案A关于属性G的直觉模糊特征信息,构建直觉模糊决策矩阵R; 步骤2:运用离差法,计算各属性客观权重l=(l1,l2,···,lm); 步骤3:运用层次分析法,计算各属性主观权重a=(a1,a2,···,am); 步骤4:根据公式(6)确定各属性的动态组合权重w=(w1,w2,···,wm); 步骤5:根据公式(2)对各方案的属性值进行聚合,得到每个方案Ai的综合属性函数ri; 步骤6:计算各方案ri的得分函数,并根据调节系数 λ的变化,确定ri的不增动态排列顺序,然后根据排序结果对方案Ai(i=1,2,···,n)进行优劣排序。 采用文献[10]中的实例,来说明所提方法的有效性。考虑一个空调选择问题。有三台空调A1,A2,A3,记为方案集A=(A1,A2,A3)。考虑三个评价属性(或因素):经济性、功能性和有效性,记为属性集G=(G1,G2,G3)。通过对用户进行问卷调查,统计分析得到方案Ai关于属性Gj的满意度uij和不满意度vij的评价结果如下: 其中属性权重的信息不完全确定, 为了确定最优的方案,下面利用本文的方法给出具体的计算步骤。 算法: 1)离差最大化法。由给出的决策矩阵R,根据公式(3)建立的单目标优化模型如下所示。 根据公式(4),解该优化模型,可得客观权重为l∗=(0.4187,0.2118,0.3695)。 2)层次分析法。根据决策者提供的对属性的偏好信息,用0.1—0.9 互补标度[12]对属性进行两两比较,得到的互补判断矩阵如下所示。 根据公式(5),可得到属性的主观权重为a=(0.2833,0.3833,0.3333)。 根据公式(6)进行组合赋权,可得 解不等式组可得 根据公式(2),计算空调系统Ai(i=1,2,3)的综合评价值函数为: 其中 计算空调系统Ai(i=1,2,3)的得分函数分别为: 因此,各方案的得分函数s(ri)(i=1,2,3)随着调节系数 λ的波动情况如图1 所示。 通过图1 可知,当0 ≤λ<0.6865时,所有空调系统的得分值大小排序为s(r1)>s(r2)>s(r3),则空调系统Ai(i=1,2,3)的优劣次序为 图1 各方案得分函数波动图 当λ=0.686 5时,所有空调系统的得分值大小排序为s(r1)>s(r2)=s(r3),则空调系统Ai(i=1,2,3)的优劣次序为 当0.686 5<λ ≤1时,所有空调系统的得分值大小排序为s(r1)>s(r3)>s(r2),则空调系统Ai(i=1,2,3)的优劣次序为 由于0.81 ≤λ ≤1,因此空调系统Ai(i=1,2,3)的优劣次序为A1>A3>A2。其中方案A1最佳,该方法的排序结果和文献[10]是一样的。相对于文献[10]中的意见集中排序法,由于意见集中排序法需要按属性根据得分函数和精确函数的大小将每个方案排成线性序;因此,对方案和属性较多的情况时会导致计算量较大,且排序过程中仅考虑直觉模糊数本身,并未考虑到犹豫度。所以从计算的复杂程度和对原始信息的利用情况来看,本文的方法更加简单有效。 在实际问题中,由于各种原因,会导致属性信息不完全确定。本文针对直觉模糊信息环境下属性权重不完全确定的多属性决策问题,提出了一种新的基于组合赋权法的多属性动态决策方法。该方法从总离差最大化原则出发,提出了一种基于单目标线性优化模型的客观属性权重确定方法。然后,结合层次分析法利用线性组合,给出了一种属性的动态组合权重的组合赋权法,该法把主观和客观两类权重信息相结合,既能充分利用客观信息,又能尽可能地满足决策者的主观偏好。最后,基于组合赋权法提出了一种新的动态决策方法,借助图像直观的展示了动态排序结果,并通过实例分析验证了该方法的有效性。并且该方法对于属性权重完全未知的问题也同样适用。2 基于组合赋权的直觉模糊多属性决策模型
2.1 直觉模糊多属性问题的描述
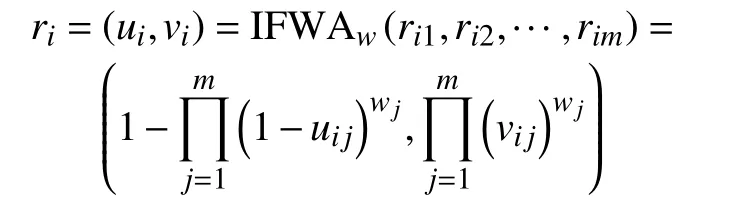
2.2 属性权重的确定
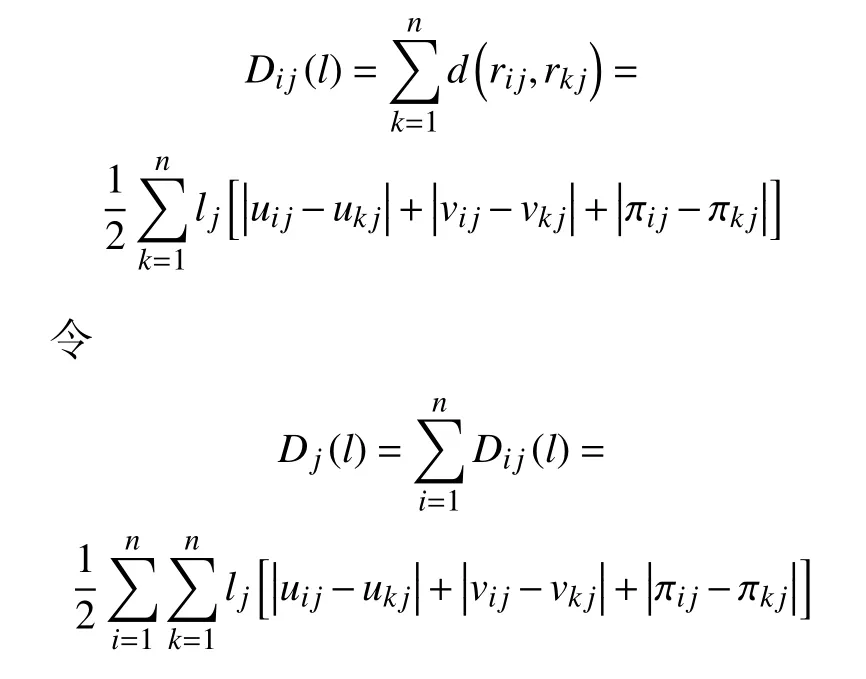

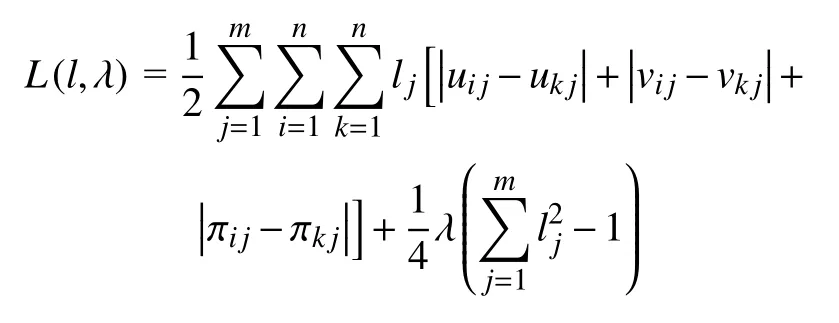


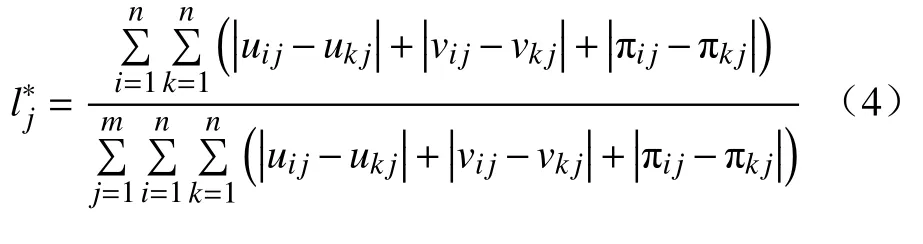
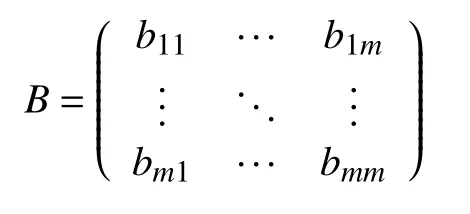

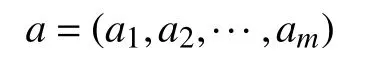
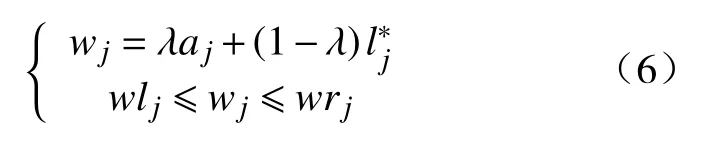
3 算例分析


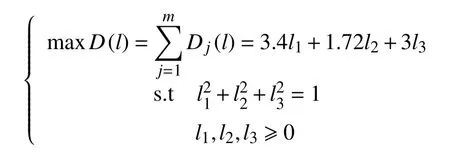







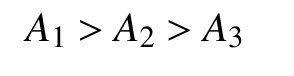
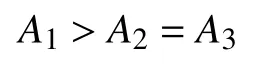
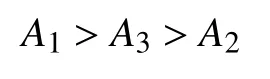
4 结论

