在区间上取值的模糊变量的可信性分布
袁敏英,孙大军
(廊坊师范学院,河北 廊坊 065000)
0 引言
Liu & Liu 于2002 年提出了一个满足自对偶性和次可加性的可信性测度[1],并于2004 年建立了可信性理论[2]。近年来,可信性理论已成为研究模糊现象的一种重要数学工具,并已成功应用到一些重要的领域[3-8]。同概率论中随机变量的概率分布一样,可信性分布[9]是可信性理论中的重要组成部分。可信性分布自2002 年Liu 提出后,引起了一些专家学者的关注。例如,文献[2]给出了可信性分布的一个充分必要条件,刻画了可信性分布的本质属性;文献[10]探讨了可信性分布的一些数学性质,并证明了模糊变量的特征函数的连续性定理;文献
[11]基于可信性分布引进了模糊占优的新概念,并讨论了模糊占优的一些基本性质。然而,除可信性分布定义之外,用可信性分布刻画模糊变量的取值规律的结论是一个空白。对比概率论中有完整的利用概率分布刻画随机变量的取值规律的系列结论,可信性理论中相关结论的缺失就更为突出,这是由于可信性测度的次可加性使得其研究比概率测度更为复杂。事实上,概率论中许多结论、公式在可信性理论中并不成立。
在可信性理论中,用可信性分布刻画模糊变量的取值规律,实质是模糊事件的可信性测度计算的理论问题。文献[1]提出模糊模拟技术,给出近似计算模糊事件的可信性测度的方法,且文献[12]中Liu Y K 证明了该方法的收敛性。尽管模糊模拟技术能用于对实际问题的近似计算,但在可信性测度的理论研究上有其局限性,且无法实现实际问题理论模型的推导。文献[13]提出可信性反演定理,给出由隶属度函数的上确界求一个模糊事件的可信性测度的方法。文献[7]基于可信性反演定理,给出几个具体的模糊事件的可信性测度的隶属度函数表达式。
在理论上,可信性反演定理对于计算模糊事件的可信性测度具有一般性、普遍性,但计算较为复杂。特别是对于简单且常见的在区间上取值的模糊变量,对比概率论中用区间端点的分布函数值来表示的结论,计算上确界就更显复杂。为此,我们提出在区间上取值的模糊变量的可信性分布问题,在一个弱条件下,推导在区间上取值的模糊变量的可信性分布表达式、条件可信性分布表达式。得到仅用区间端点的可信性分布函数值表示模糊事件的可信性测度的等式。从而为应用可信性分布处理实际问题,特别是为建立和推导实际问题的理论模型,给出重要的理论支撑。
1 预备知识
定义1[1]设Θ 是一非空集合,P( Θ )为Θ 的幂集。Cr是定义在P( Θ) 上的集函数。如果Cr满足以下四条公理,则称Cr是一个可信性测度。
理1 (规范性)Cr{Θ } =1。
公 理2 (单 调 性) 如 果A⊂B,则 有
公理3 (自对偶性) 对于任何A∈P( Θ ),
公理4 (极大性) 对于任何Ai∈P( Θ ),若
定义2[13]一个模糊变量就是指从可信性空间到实数集上的函数。
定义3[9]模糊变量ξ的可信性分布定义为
显然,Φ是单调增函数。
定 义4[13]设ξ是 定 义 在 可 信 性 空 间 上的模糊变量。那么由可信性测度Cr可以导出其隶属度函数为
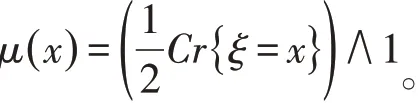
定理1[14]设Θ为一个非空集合,P( Θ )为Θ的幂集,Cr是可信性测度,则对于任意A,B∈P( Θ) 有
定理2[14]设Θ为一个非空集合,P( Θ) 为Θ的幂集,Cr是可信性测度,则对于任意A,B∈P( Θ )有
定理3[2]可信性测度Cr是次可加的,即对于任意A,B∈P( Θ )有
定理4[13](可信性反演定理)设ξ是由隶属度函数μ表示的一个模糊变量,则对实数集的任意子集B,成立
定义5[14]设可信性空间(Θ,P( Θ ),Cr),对任意A,B∈P( Θ) ,称在事件B下事件A的条件可信性测度为:

当Cr{B} >0时
2 模糊变量的可信性分布
以下主要讨论在区间上取值的模糊变量ξ的可信性分布表达式。
引理1 设ξ为模糊变量,Cr是一可信性测度,若则 当时,有Cr{ξ>x+t}<0.5成立。
另外,当Cr{ξ≤x}<0.5时,Cr{ξ>x+t}只有两种取值结果:Cr{ξ>x+t}≤0.5 或Cr{ξ>x+t}≥0.5。从而有下面的引理:
引理2 设ξ为可信性空间上的模糊变量,Cr是一 可 信 性 测 度 ,x,t(t>0 )∈ℜ, 若只有三种取值组合:定理5 设ξ为模糊变量且可信性分布函数为Φ,x,t(t>0 )∈ℜ,若Cr{ξ≤x}≠Cr{ξ≤x+t},则有

证明:简记:

由引理2知a和c只有三种取值组合:

以下分别对这三种情况进行讨论:
(1)a<0.5,c≤0.5
由a<0.5,c≤0.5 及 定 理 3 得 ,进一步由这个不等式及定理 2 得,从而由公理1和公理3得,

由a≥0.5,c<0.5 及 公 理3 和 定 理1 得,
所以这里只有b≥c一种情况,此时又因为从 而 有故
(3)a<0.5,c≥0.5
由c≥0.5 及 公 理 3 得,Cr{ξ≤x+t}=1-Cr{ξ>x+t}≤0.5,从 而 由 定 理1 得于是有
当a≤b时 , 有时 , 有Cr{ξ>x+t}=Cr{ξ≤x+t},与假设矛盾。所以这里只有a≤b一种情况,此时又从而有Φ(x+t),故
推论1 设ξ为可信性空间上的模糊变量,若其分布函数Φ(x)=Cr{ξ≤x} 严格单调增,则对任意区间(a,b]有成立。
如果去掉定理5 的假设条件,不难得到与文献
[14]定理1.13类似的结果。即:
性质1 设ξ为模糊变量,其可信性分布Φ,则对任意区间(a,b]有Φ(b) -Φ(a) ≤Cr{a <ξ ≤b} ≤Φ(b) ∧(1-Φ(a) )。
例1 设模糊变量ξ的隶属度函数为
因此有

同理
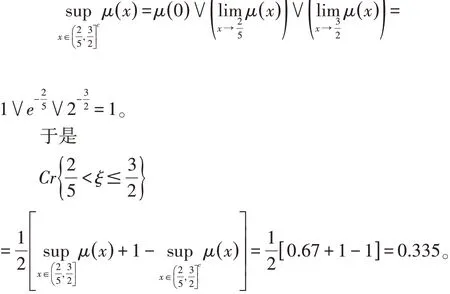
显然,方法一比方法二要简便。
基于定理5,可进一步给出条件可信性分布函数表达式。
定理6 设ξ为模糊变量且可信性分布为Φ,假设则 有


为进一步简化上式,进行以下分析:
3 结语
可信性分布是刻画模糊变量取值规律的函数,一般情况下,在区间上取值的模糊变量没有可信性分布表达式。本文增加了一个较弱的条件,得到了在区间上取值的模糊变量的可信性分布表达式及条件可信性分布表达式。使得可信性测度的计算由复杂的求上确界变为简单的求函数值,也为应用可信性分布处理实际问题,特别为建立和推导实际问题的理论模型给出重要的理论支撑。

