一道全国大学生数学竞赛题的引申与推广
郑华盛, 袁达明,2
(1.南昌航空大学 数学与信息科学学院,南昌 330063; 2.江西师范大学 数学与统计学院,南昌 330022)
1 引 言
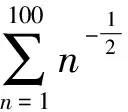
本文旨在将该和式取整问题作进一步地引申和推广,探讨有关和式不等式与极限新题的构造问题.该问题的研究对于创新思维和创新意识的培养具有一定的意义.下面,首先给出该和式的不等式命题,然后进一步推广到其它几类和式情形,得到几个相关命题,之后,再利用所得命题,构造和编制一系列关于和式的极限及不等式的新题.
2 几个相关结论
命题1设m,n为两个任意给定的正整数,m 或 或 命题2设m,n为两个任意给定的正整数,m (i)当α≠1时,有 或 或 (ii)当α=1时,有 或 命题3设m,n为两个任意给定的正整数,m 或 更一般地,由积分和与定积分的几何意义及凹凸弧的性质,可得 命题4设m,n为两个任意给定的正整数,m (i)当f(x)在(0,+∞)上非负且严格单调减少时,有 或 而当f(x)在(0,+∞)上非负且严格单调增加时,上述不等式反向成立. (ii)当f(x)为(0,+∞)上的凹弧时,有 而当f(x)为(0,+∞)上的凸弧时,不等式反向成立. 而S100-1<[S100]≤S100,于是17<[S100]<19,故[S100]=18. 类似地,可求如下和数x的整数部分[x]: 此外,利用以上命题,可构造和编制一些有关和式的极限与不等式新题. 由命题2和命题3及夹逼准则,可得一些和式极限: 从而可构作如下对应的极限新题: 即 于是得 从而可构造一类极限新题 其中常数α≥0,β>0或α>0,β≥0. 于是数列{an}单调减少且有界,故又可构造如下极限新题: 由此可构造如下极限新题: 类似地,由命题4,选取不同的f(x),还可构造和编制出一系列的和式极限新题. 利用以上命题2,也可编制一些有关和式不等式的新题.如: 取α=2,m=1,则有 取α=2,m=2,则有 或 从而 取α=2,m=3,则有 或 即得不等式 特别地,当m=1时,有 特别地,当m=1时,有 由该不等式也可构造极限新题:当0<α<1时 类似地,通过选取不同的函数f(x),由命题4可编制出一系列的和式不等式新题. 本文对一道关于和式取整的全国大学生数学竞赛试题进行了引申和推广,通过构作相应的辅助函数,利用函数的单调性与凹凸性,结合积分和与定积分的几何意义,得到了几类和式的不等式命题,之后,探讨了如何利用这些命题构造和编制和式的极限与不等式新题,并给出了一些应用实例.如此过程,不仅拓展和丰富了和式的不等式与极限新题的构造方法,而且对于培养和提高学生的探究能力与创新能力具有一定的促进作用.读者也可以动手类似地构作一些有关和式不等式与极限的新题. 致谢作者非常感谢所引文献对本文的启发及审稿专家提出的宝贵意见.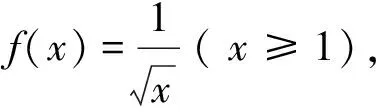
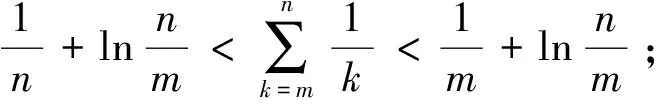
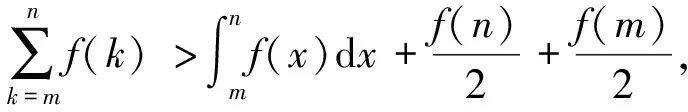
3 赛题的求解及和式极限与不等式新题的构造
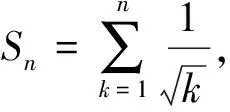
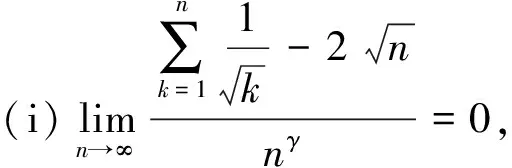
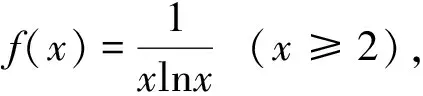
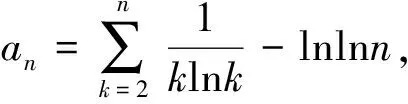
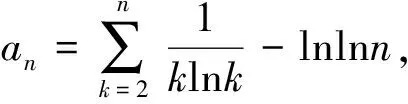
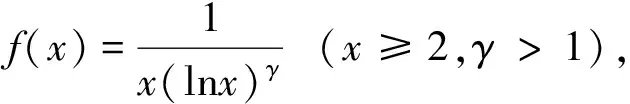
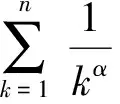
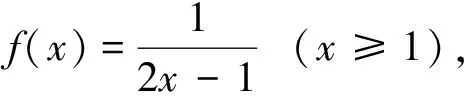
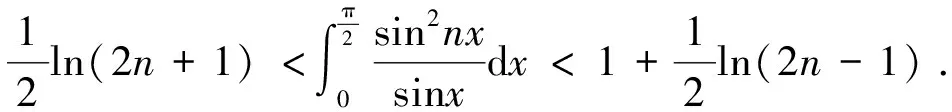
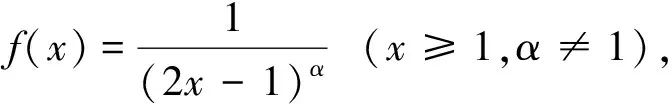
4 结 论

