等比法求和式极限

郭 伟

（长治学院 数学系，山西 长治 046011）

1 预备知识

在高等数学中，经常会遇到一些计算和式极限[1]的题型。由于极限的四则运算对和式极限是不成立的，我们可以将和式放大与缩小并借助于夹逼准则求一些特殊的和式极限，但很多情况下夹逼准则是不成立的。定积分的引入对计算和式极限提供了一个较好的方法[2]。众所周知，定义在[a，b]上的定积分

在函数可积的条件下，通常采取等分法和特殊取点法来计算定积分，例如将[0，1]区间n等分，并取ξi为区间的右端点，则

反过来，和式极限可以借助于定积分来计算，从上述两个例子可以看出，等式最右端是一和式极限。这类极限有个基本的特征，是将区间等分来计算，即例子中的可以提取到求和符号之外，教材上主要介绍将这类和式极限转化成定积分计算。例如：

2 等比法计算和式极限

2.1 基本思想

设f（x）是定义在[1，b]上的连续函数，在[1，b]上插入n-1个特殊分点，依次为

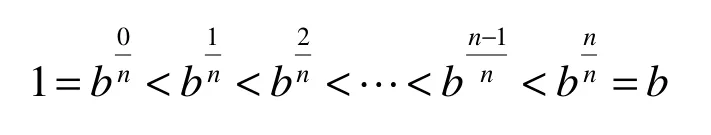
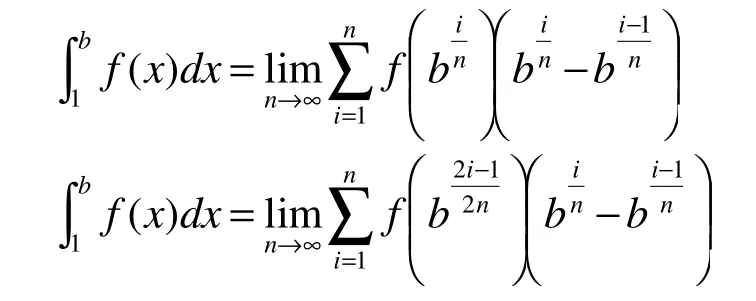
2.2 应用举例

解：这是一个和式极限的问题，借助于定积分的定义可得：

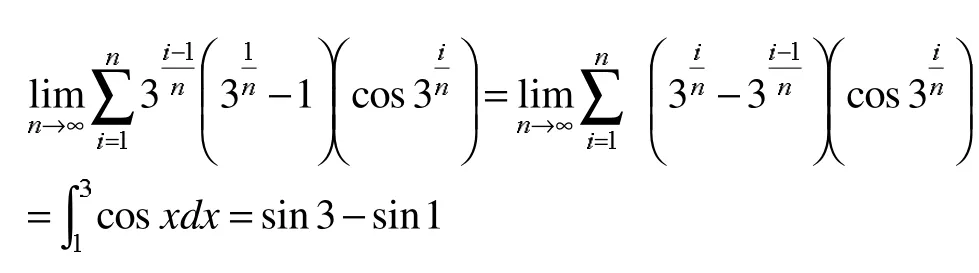
2.2.2 计算

2.2.3 计算

小结

在计算和式极限时，我们首先将和式极限化为最简单形式，从表达式观察分割和取点的情况，然后转化为定积分来计算，但如果是任意分割区间，取点不取端点和比例中项（例如取中点等），定积分则化为更复杂的和式极限。