一类交错级数求和的探讨及其推广

杨传富, 代 成

(1.南京理工大学 应用数学系,南京 210094； 2.南京理工大学 宣传部,南京 210094)

1 引 言

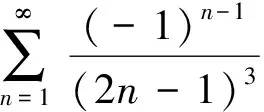
该题对学生来说容易下手，因为已经提示将给定函数进行正弦展开，然后在此基础上再求给定级数的和.将函数f(x)作周期为2π的奇延拓，再进行正弦展开，则

由于函数f(x)为连续函数，所以其正弦级数为

即

创新思维能力的培养是多途径的，在解题中培养学生创新思维能力是一条有利途径.解题中应创设问题情景、激发创新思维对题目采取多种解法，开拓学生的解题思路和视野[1].教会学生分析如何解题，提出解决问题的关键途径，从而得出解决问题的方法.激发学生发散思维，引导学生将问题与所学知识有机联系在一起，大胆联想、通过一些探索，得出期望的结果.

正如著名数学家、教育家苏步青所说：“学习数学要多做习题，边做边思索.先知其然，然后知其所以然.”因此，要求学生在解题过程中注重获得更多启示，从而在数学解题中培养学生的创新思维能力.

联想

右边出现需要的n-3因子，所以尝试将f(x)=x2(0

因此

利用(4)得

(1)

试将f(x)=x4(0

因此

运用(1)和(4)得

(2)

为此，对f(x)=x6(0

因此

运用(1),(2)和(4)得

(3)

注意到将函数f(x)=1(0

即

(4)

3 结 语

本文用构造的简单幂函数的傅里叶级数展开已求得

以上只是结合自己的教学实践，从一道交错级数求和问题出发，加以问题引申对学生创新能力培养的一点做法.高等数学教学内容丰富，在教学中教师多为学生设计一些新颖有趣的问题[2-4], 让学生勤思考，多联想，这既能充分调动学生学习的主动性，又能培养学生的创新能力.

致谢作者感谢审稿专家的有益建议.