梯度的几何意义

严质彬

(哈尔滨工业大学(深圳)理学院，广东 深圳 518055)

1 引 言

数学教学和研究中, 追求几何意义, 一般是指借助几何对象, 来解释数学概念及数学命题的形象化的直观的含义.目前在数学分析和高等数学课程的教学中, 梯度作为向量, 解释其几何意义一般是引入等高线(等值面)这个几何对象[1-3]: 梯度向量的方向是等高线的法方向(指向高度上升的那一侧)；梯度向量的大小是该方向的方向导数.这当然是一个很好的几何解释, 能增加对梯度概念的形象化的认识.关于梯度的教学, 近年来也还有一些有趣的研究[4-5].

在进行多元微积分的教学时, 已经学习过向量与矩阵.与一元函数的导数相对应的多元函数的概念不是偏导数, 而是梯度.多元函数的梯度, 或者一般地, 多元向量值函数的雅可比矩阵, 是一元函数的导数的高维类比[2].这个思想在数学分析和高等数学的教学实践中在不断地强化.

一元函数的导数的几何意义是切线的斜率.斜率联系着倾斜角这个非常形象直观的几何对象.既然梯度是导数的高维类比, 那么梯度的几何意义能不能也结合切平面, 倾斜角这些几何对象来说明呢? 除了用等高线这个几何对象以外, 还能不能用其他几何对象来解释梯度的几何意义呢?

2 平面倾斜度的向量刻画

回忆立体几何中二面角的概念.二面角是指三维空间中, 从一条直线出发的两个半平面所组成的图形.这条直线叫做二面角的棱, 这两个半平面叫做二面角的面.以棱上的一点为端点, 在两个面内分别作垂直于棱的两条射线, 这两条射线所成的角叫做二面角的平面角.二面角的平面角的角度大小, 简称为二面角的角度大小.引入二面角的角度大小的概念, 可以将一个平面相对于另一个平面的位置关系用数量化的方法来描述.下面来解释, 只用二面角的角度大小这一个数量指标, 是不能完全刻画两个平面的相对位置关系的.

先观察平面上两条直线的相对位置关系的刻画.在平面解析几何中, 有直线的“点斜式”方程.设直线l过点(x0,y0), 直线l的上升方向(可用直线l的位于x轴上方的那一半射线来代表)和x轴正方向的夹角为θ(不考虑θ为直角的情形), 直线l相对于x轴的斜率定义为k=tanθ.于是直线的“点斜式”方程为y=y0+k(x-x0).因此, 一条直线可以由两个要素来完全定位: 它上面的一个点, 以及它相对于给定参考直线的斜率.

再来观察三维直角坐标空间中的一个平面, 它与xOy坐标平面既不平行也不垂直.该平面位于xOy坐标平面上方的那个半平面与xOy坐标平面构成两个互补的二面角, 记其中的一个为θ.尽管tanθ能够在一定程度上反映该平面相对于xOy坐标平面的倾斜度, 但显然不能通过两个要素(平面上的一点, 及tanθ)来完全定位该平面: 这两个要素只能将平面确定到相差一个旋转的程度.总结这个事实, 说三维空间中, 一个平面相对于xOy坐标平面的二面角的正切值, 不是二维平面中, 一条直线相对于x轴的斜率这个概念的正确类比.那么, 正确的类比是什么呢?

定义1给定三维空间中的平面Λ, 它与xOy坐标平面既不平行也不垂直.考虑Λ的位于xOy坐标平面上方的半平面与xOy坐标平面所成的角度大小为锐角的那个二面角.该二面角的角度大小记为θ；垂直于该二面角的棱, 位于该二面角的水平的面内的射线记为l.则以tanθ为长度大小, 以射线l为方向的xOy坐标平面内的二维向量称为平面Λ相对于xOy坐标平面的斜率, 记为k.

注1 若平面Λ与xOy坐标平面平行, 则Λ相对于xOy坐标平面的斜率规定为xOy坐标平面内的二维零向量(注意零向量没有方向); 若平面Λ与xOy坐标平面垂直, 则Λ相对于xOy坐标平面的斜率无定义.

任何一个不垂直于水平面的平面, 可以由它上面的一个点, 及它的斜率向量, 这两个要素来唯一确定.为了后面讨论梯度的需要, 用解析几何的语言来陈述这个事实.

定理1给定空间中的一个平面Λ.则Λ具有方程

z=z0+a(x-x0)+b(y-y0)

(1)

的充要条件是

(i)点(x0,y0,z0)∈Λ；

(ii)Λ的斜率k的直角坐标为(a,b).

下面的引理可用立体几何知识证明, 这里从略.

引理给定三维空间中的平面Λ, 它与xOy坐标平面既不平行也不垂直.则Λ的任一条法线在xOy坐标平面的投影垂直于Λ与xOy坐标平面的交线.

为方便起见, 向量k的直角坐标为(a,b)这个事实简记为k=(a,b).

定理1的证明充分性 首先, 由条件(ii)知Λ有斜率向量, 于是由定义1及注1知Λ不垂直于xOy坐标平面.

若k=(a,b)=(0,0), 则由注1知Λ平行于xOy坐标平面, 再由条件(i)知Λ有方程z=z0, 从而结论成立.

若k=(a,b)≠(0,0), 则由定义1知Λ不平行于xOy坐标平面.首先, 由定义1, 位于xOy坐标平面内, 与k=(a,b)垂直的平面向量, 例如(-b,a), 平行于Λ与xOy坐标平面的交线(定义1中所说的二面角的棱), 从而平行于平面Λ.平面向量(-b,a)置于三维空间中, 就是(-b,a,0).另一方面, 在定义1中, 射线l绕端点向上旋转θ角得到的射线位于平面Λ内.由条件(ii), 这里θ满足

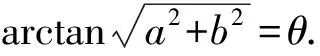
(-b,a,0)×(a,b,a2+b2)=(a(a2+b2),b(a2+b2),-(a2+b2)).

即为平面Λ的一个法向量.由此及条件(i)写出平面Λ的点法式方程, 整理即得方程(1).

必要性x=x0,y=y0,z=z0满足方程(1), 因此(i)成立.若(a,b)=(0,0), 由方程(1),Λ平行于xOy坐标平面, 从而由注1,(ii)成立.下设(a,b)≠(0,0).由方程(1),(-a,-b,1)是Λ平面的指向上方的一个法矢量.由立体几何易知, 定义1中所说的二面角的角度θ等于Λ的指向上方的一个法矢量与z轴正方向矢量(0,0,1)的夹角.因此

(2)

又由引理1, 知Λ的指向下方一个法矢量, 如(a,b,-1), 在xOy坐标平面内的投影向量(a,b,0)与定义1中所说的射线l有相同的指向.因此按定义1, 斜率向量k与xOy坐标平面内的向量(a,b)有相同的方向.另一方面,(2)式说明k与向量(a,b)有相同的长度大小.因此k=(a,b).证毕.

注2 按照定义1和定理1, 当把平面相对于xOy坐标平面的斜率理解为向量时, 就可以完全合理地称方程(1)为平面的“点斜式”方程.

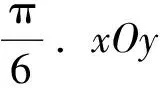
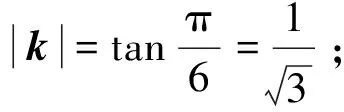
于是, 斜率向量k的坐标为

因此由定理1的充分性, 平面Λ的方程为

3 与直线斜率的联系

细心的读者可能已经注意到, 定义1中的二面角取的是xOy坐标平面上方的两个二面角中角度为锐角的那个.而平面解析几何中, 定义直线的斜率的那个角可以是钝角的: 直线位于x坐标轴上方的射线与x轴正半轴射线的夹角.现在来解释这个不一致性.

若坐标平面上的一条直线l的斜率为-3, 按通常的理解, 就是指l的位于x坐标轴上方的射线(指向l的上升方向)与x轴正半轴射线的夹角为π-arctan|-3|, 它是钝角.现在按照定义1的精神, 把斜率-3理解为一维实空间中的向量, 则它的长度大小为|-3|=3, 方向单位向量为-1, 也就是指向一维实空间x坐标轴负方向的单位向量.这样锐角arctan|-3|就是l的上升方向与x坐标轴上的这个单位向量的夹角了.一句话, 按照把斜率理解为向量的精神, 直线的斜率应理解为一维向量, 由于作为参考方向的一维单位向量可能是1, 也可能是-1, 因此, 平面上直线相对于的x坐标轴的倾斜角也总可以理解为锐角.

由于一维实空间只有有限个(两个)单位向量, 所以人们很容易从一开始就不加思索地选择固定的一个(x轴上的正向单位矢量)作参考来度量任意一条直线的倾斜程度.平面上有无穷多个单位矢量, 选择一个以不变应万变的单位向量作参考, 来度量任意平面的倾斜程度, 直觉告诉我们, 这是行不通的.这大概是“平面的斜率”这么初等的思想, 到目前为止, 文献中还没有用严格的数学语言陈述过的心理学障碍吧.本文的工作表明, 把斜率理解为向量, 即使是直线的斜率也理解为向量(一维空间中的向量), 就能越过这个障碍.

4 梯度的几何意义

定理2二元函数z=f(x,y)在(x0,y0)处可微.则z=f(x,y)在(x0,y0)处的梯度(f′x(x0,y0),f′y(x0,y0))等于z=f(x,y)的图像在点(x0,y0,f(x0,y0))处的切平面相对于xy坐标平面的斜率.

证由切平面的方程为

z=f(x0,y0)+f′x(x0,y0)(x-x0)+f′y(x0,y0)(y-y0),

定义1, 及定理1即得.证毕.

5 结 论

完整地描述空间中一个平面相对参考平面的倾斜度的数学概念是斜率向量.二元函数的梯度是切平面相对于水平面的斜率向量.

致谢感谢审稿人对本文的仔细阅读和提出的修改意见.