从格林公式的两种形式看向量场积分的统一性

徐 松， 王 伟， 周彩莲

(宁波大学 数学与统计学院，浙江 宁波 315211)

1 引 言

格林公式、斯托克斯公式和高斯公式是多元积分学中三个重要的公式，揭示了曲线积分、曲面积分和重积分三者之间的关系，构成多元积分理论的中枢[1-2].它们之间有着紧密的联系，在一定的条件下可以互相转化来求解问题[3-5].一般的微积分教材只给出格林公式的一种分量形式，简单地指出斯托克斯公式和高斯公式是格林公式的推广，但究竟如何推广以及它们之间的内在逻辑关系等，很少有专门的论述.这使得学生在学习过程中往往只具备碎片化的知识，很难从整体上理解这些公式，只能死记硬背.这些内容成为教学上的难点和学生学习的痛点.

微积分基本公式是微积分学最重要的公式，它建立了微分学与积分学之间的联系.从向量场积分的角度来看，它与格林公式、斯托克斯公式和高斯公式本质相同，都是揭示场在区域内部与边界之间的性态关系[6-7].那么，能否用统一的定理来描述微积分基本公式和向量场积分公式，使得每个公式都是统一性定理的不同形式呢？运用这种统一性的观点来组织教学，会加深学生对整个微积分学内容和结构的认识，增强学生分析归纳能力，提升学生的整体感和大局观能力.而这些讨论在一般的微积分教材中也少有涉及.

基于上述考虑，从格林公式两种等价的向量形式出发，将它们推广至空间向量场，指出它们与斯托克斯公式和高斯公式之间的一一对应关系；并基于此，从统一性视角给出微积分基本公式、格林公式、斯托克斯公式和高斯公式的一般形式——统一化积分定理.从这种统一性观点来展开教学，不仅能让学生深入理解多元积分学中的三大公式，还能让他们从更高观点和整体的视角来理解整个微积分课程，提升数学素养和格局.

2 格林公式的两种形式

将给出格林公式的切向量和法向量形式，为此先引入向量场的散度和旋度的概念.

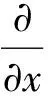
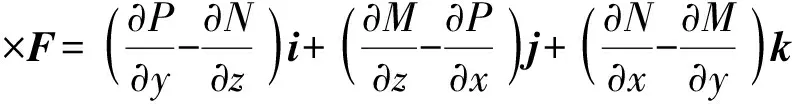
为F在点(x，y，z)处的旋度或环量密度.

设平面向量场F=Mi+Nj，形式上它可写为F=Mi+Nj+0K，则格林公式的切向量形式可表示为

∮CF·Tds=∬D∇×F·KdA，

(1)

其分量形式可写为一般微积分教材中常见的形式

(2)

其中简单闭曲线C为区域D的正向边界曲线，T为C在点(x，y)处的单位切向量.

格林公式的切向量形式表明，向量场F绕曲线C的环流量等于F的旋度的K分量在闭区域D上的二重积分，所以该形式也称为环量—旋度形式.

格林公式的法向量形式可表示为

∮CF·nds=∬D∇·FdA，

(3)

其分量形式可写为

(4)

其中n为闭曲线C在点(x，y)处的单位外法向量.

格林公式的法向量形式表明，向量场F穿过曲线C向外的通量等于F的散度在闭区域D上的二重积分，所以该形式也称为通量—散度形式.

格林公式这两种形式是等价的.事实上，对场G=-Ni+Mj应用公式(1)即得到公式(3).对场G=Ni-Mj应用公式(3)即得到公式(1).

3 格林公式在三维向量场上的推广

下面将讨论平面向量场上格林公式的两种形式与三维向量场上斯托克斯公式和高斯公式之间的一一对应关系.

设空间向量场F=Mi+Nj+PK，斯托克斯公式可表示为

∮CF·Tds=∬S∇×F·ndσ，

(5)

其中曲线C为定向曲面S的边界，n为S在点(x，y)处的单位法向量，C的正向与n成右手系.

斯托克斯公式表明，向量场F绕定向曲面S的边界曲线C正向的环流量等于F的旋度在闭区域D上的二重积分.

比较公式(1)和(5)可以看出，将格林公式的平面积分区域D改为空间曲面积分区域S，D的单位法向量即Z-轴正向单位向量K改为S上任一点的单位法向量n，以及平面面积元素dA改为空间面积元素dσ，格林公式即推广为斯托克斯公式.所以，斯托克斯公式是格林公式的切向量形式从平面到空间的直接推广，二者形式几乎完全一致.

下面考虑格林公式与高斯公式之间的联系.高斯公式可以表示为

SF·ndσ=∭D∇·FdV，

(6)

其中D为闭曲面S所围成的闭区域.

高斯公式表明，向量场F通过闭曲面S的向外流量等于F的散度在闭区域D上的三重积分.

比较公式(3)和(6)可以看出，将格林公式左边在闭曲线C上的曲线积分改为闭曲面S上的曲面积分，弧长元素ds改为面积元素dσ，以及右边在闭曲线C所包含的平面区域D上的二重积分改为闭曲面S所包含的立体区域D上的三重积分，格林公式即推广为高斯公式.所以，高斯公式是格林公式的法向量形式从平面到空间的直接推广，二者形式高度一致.

通过以上分析，格林公式的两种形式与斯托克斯公式及高斯公式之间的关系见图1.

图1

教师如果能在课堂上分析这三个重要积分公式之间的关系，展示推广的思维过程，学生能更容易地理解这些这些公式，在实际解题中可以灵活运用它们，而不用孤立、死记硬背地去学习.

例1设函数f和g在以曲线C为边界的定向曲面S上有一阶连续的偏导数，证明：

∮Cf∇g·Tds=∬S(∇f×∇g)·ndσ.

证由斯托克斯定理得

∮Cf∇g·Tds=∬S(∇×f∇g)·ndσ=∬S(∇f×∇g+f∇×∇g)·ndσ，

又∇×∇g=0，故原式成立.

例2设函数f和g在由闭曲面S所围成的区域D上具有连续的二阶偏导数，证明：

∬Sf∇g·ndσ=∭D(f∇2g+∇f·∇g)dV.

证由高斯定理得

Sf∇g·ndσ=∭D∇·(f∇g)dV=∭D(f∇2g+∇f·∇g)dV.

4 统一化积分定理

下面将给出微积分基本公式与向量场积分公式的统一化描述.

设函数F(x)在闭区间[a，b]上可微，微积分学基本公式可表示为

(7)

令F=F(x)i，积分区间[a，b]在边界即左右端点a与b处的外法向量分别为na=-i与nb=i，则式(7)可改写为

(8)

从公式(8)可以看出，微积分学基本公式表示微分算子∇与场F在区间[a，b]上作点积运算的积分等于场F在边界(即端点)处法向分量的和.

如果把线积分与面积分理解为“和”，则与微积分基本公式一样，格林公式的法向量形式(3)与高斯公式(6)均表示算子∇与场F在区域上作点积运算的积分等于场在区域边界处法向分量的和.

类似地，格林公式的切向量形式(1)与斯托克斯公式(5)表示微分算子∇与场F在一区域上作叉积运算的积分等于场在区域边界处切向分量的和.

这样，微积分学基本公式与格林公式、斯托克斯公式和高斯公式可以统一地描述为如下统一化积分定理[7]：

定理1微分算子对场作用后在某一区域上的积分等于场在该区域边界上适当分量的和.

统一化的积分定理表明，微积分学基本公式和向量场积分公式本质相同，都是描述场在区域内部与边界上性态关系.

教师如果在章节小结课上用这种统一性的观点来开展教学，不仅能让学生对向量场积分有更深入的理解，而且对整个微积分学有了更高观点的认识，体会数学“殊途同归”“万变不离其宗”的哲学思想，领略数学的简约与大气之美.

5 结论与认识

在微积分的学习过程中，格林公式、斯托克斯公式和高斯公式等内容非常晦涩抽象，学生不容易理解掌握这些公式，很难做到灵活运用.文章指出向量场上斯托克斯公式和高斯公式分别是格林公式切向量和法向量形式从平面到三维空间的直接推广，给出微积分基本公式与向量场积分公式之间的本质属性.教师如果能在讲完这些内容后，安排适当的课时，分析从格林公式推广到斯托克斯公式与高斯公式的具体过程，归纳它们之间的逻辑关系，这将有助于学生理解掌握这些公式.如果再能从统一性观点出发，阐述微积分基本公式与向量场积分公式之间的共同本质属性，将进一步加深学生对微积分这门课程的整体认知，提升他们的数学素养和格局.

致谢非常感谢相关文献对本文的启发以及审稿专家和编辑提出的宝贵意见.