基于排队论模型的机场出租车问题研究
张家怡, 余晓养, 夏志乐
(台州学院 数学系,浙江 临海 317000)
1 引 言
目前,乘坐出租车是乘客到达目的地的主要交通方式之一,其便利性正日益成为许多城市的显著流动模式[1-5].机场的乘客若想“打车”需去“乘车区”,此时,管理人员将分批放行一定数量的出租车到该区域.因此,机场的服务水平一定程度上影响着到达机场出租车司机的决策,“载客返市”或“空车返市”,即
(A)司机在机场蓄车池等待下一乘客返回市区,其中等待时间与乘客数量及蓄车池中排队的出租车数量成正比;
(B)司机到达机场后,不继续载运乘客,直接返回市区进行拉客,但其需承担这段路程的车油费及放弃的潜在利益.
一般情况下,到达机场的出租车司机可以得到该时段的航班情况及蓄车池中出租车数量的信息,再根据自己的个人经验(如淡、旺季航班及乘客数量)作出决策.在现实生活中,影响司机作出决策的因素有很多且效果各异.因此,有必要建立具体的数学模型,定量分析各种因素,优化出租车服务系统.近年来,城市出租车问题得到了广泛的研究,文献[1]以北京站为例,利用费用决策模型对多点并列式出租车排队服务系统的服务台数进行了数量优化;文献[2]利用GooSeeker抓取某一城市的出租车数据,运用排队论建立了供需匹配模型,分析了不同时空出租车资源的“供求匹配”程度;针对城市道路系统实际情况,Zhang等[3]提出了一种能够满足道路通行能力的通用多服务器M/M/c排队模型,并讨论了排队模型的稳态分布和渐近性质;Sayarshad等[4]使用纽约出租车数据,基于排队论模型,提出了一种新的预测出租车未来需求及运行状态.Ramezani等[5]从宏观层面研究了城市出租车调度的建模问题,提出用宏观基本图方法来表示交通状况的动态演变.以上结果表明,出租车服务系统的缺乏将导致出租车闲置严重积聚,提高出租车服务性能能有效降低交通拥挤,提高司机的收益.以上文献主要研究市区出租车问题,实际中,往返机场和城市间的乘客数量越来越多,因此有必要研究往返于机场和城市间的出租车面临的问题,即“载客返市”“空车返市”两种决策下司机收益的情况.
基于以上讨论,本文研究往返于机场和城市间出租车司机“载客返市”和“空车返市”两种决策下的收益情况,与已有文献相比,创新点如下:
(i)研究往返于机场和城市间出租车司机作出决策的机理,同时考虑乘客数量和司机收益两个方面,为出租车司机建立合理的决策模型并给出策略方案;
(ii)通过爬虫技术从携程网中搜集某机场的相关数据及该城市出租车数量,为该机场的出租车司机设计方案,并检验其合理性;
(iii)在保证交通安全的情况下,以提高某机场拥有两条并行车道的“乘车区”的效率为目的,设置上车点并合理安排出租车及上车乘客;
(iv)为了平衡司机的收益情况,为机场设计合理的安排方案,给予一些短途载客司机一定的“优先权”.
本文研究问题来源于2019年全国大学生数学竞赛C题.
2 问题描述
2.1 问题一描述
影响司机作出等待客人或空车返回市区的策略选择的因素很多,因此,从主要因素即司机收益状况入手,进行分类讨论:
(i)当选择乘坐出租车的乘客数量多于等待的出租车数量时,利用排队论中的先到先服务的原则对选择待客决策的司机收益情况进行分析;接着再考虑“放空”返市的决策的收益情况,先是根据泊松分布预估司机返回市区时所接客的波数,其次,通过出租车的价格表及单位里程消耗的油费,计算出司机的收益情况,最后比较两种情况的收益数,为司机作出合理的选择决策;
(ii)当选择乘坐出租车的乘客数量少于等待的出租车数量时,可如上对“载客返市”及“空车返市”两种情况进行分析比较,得到决策模型.
2.2 问题二描述
问题二是在问题一模型的基础上进行求解的,但问题二需要结合实际情况进行分析.因此,先收集上海浦东国际机场的相关信息,即航班信息、该机场飞机的平均客座率及该城市的出租车收费表、机场到市区的大致距离,再利用第一题的方法建立模型,依据实际情况中司机到达机场时的时间、机场乘客数及等待客人的出租车数量,通过Matlab计算该种情况下载客与放空的收益结果并进行比较,由此为机场出租车司机设计合理的方案.
2.3 问题三描述
问题三需要为机场设计合理的“上车点”,使得在保证交通安全的情况下,提高机场的乘车效率.因此,在设计方案时,充分考虑交通拥堵、乘客上出租车的方位等问题,绘制出并行车道为X形立桥的示意图,并建立乘车效率模型的示意图.
2.4 问题四描述
对于问题四,从平衡出租车司机之间的收益角度出发,考虑短途载客司机的优先权问题,引入排队模型的优先服务权规则理论,对各时段内平均机场司机数量进行 5 等份,然后依据各等分的司机往返时间即从载客离开“乘车区”开始算起到返回“蓄车池”截止的时间段进行设计方案,往返时间越短的出租车赋予的优先级越高,令相应的优先级对应所标识的车道,且优先级越高距离“乘车区”越近,有优先进入“乘车区”的特权,优先级最低的同当日还未再过客的出租车安排在同一车道,因此,可得机场的设计方案.最后通过计算第k级优先级的出租车司机的平均等待时间和平均队长,预估该系统优先权对出租车司机排队等待模型的影响,来检验该方案的合理性.
3 模型建立
3.1 问题一模型的建立
影响出租车司机决策的因素有:排队的出租车数量、机场下飞机乘客的数量、机场到市区所需时间等.为给出租车司机设计合理的选择策略,考虑从出租车司机的收益情况出发,通过比较分析某时间点乘客数量和此时正在排队等候载客的出租车数量,讨论分析以下两种情况:
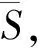
若从司机所在地到达乘客目的地的距离为S′,则乘客乘坐出租车的价格为
(1)
若司机依照先到先提供客源的排队安排进行等候,则令其花费的待客时间为xM,载客返回到市区时间为St0,那么司机在xM+St0长的时间得到的收益为Q1=W-SL.
若出租车司机不载客,选择直接花费St0时间返回市区并在市区继续接客.而司机在市区接到乘客的情况为排队论中的最简单流的输入,即在一定时间间隔内,司机接到k波乘客的概率仅与这段时间的长短有关,故具有平稳性;在时间区[t,t+Δt]内来到k个乘客的概率与时间t之前来多少乘客无关,故具有无后效性;且在瞬时内只能有一波乘客到达,不可能有两波及两波以上顾客同时到达,故具有普遍性.在满足以上三个条件后,可知在时间t内司机能接到k波乘客的概率服从泊松分布[11],即为
其中参数μ表示单位时间内到达乘客的平均数,当Δt充分小后,在[t,t+Δt]时间内无顾客到达的概率为v0(Δt)=e-μt≈1-μΔt.
其中,k1指在“供不应求”放空返回市区状态下,在时间xM下,以90%的概率预估司机可能接到的乘客数.
第二种情况,当该时间点乘客数量小于此时“蓄车池”里的车辆数,即表现为“供过于求”.通过查阅的相关数据[7]发现,一般情况下,一批航班抵达机场的乘客人数K中在白天和晚上选择出租车的比例相对稳定,设该比例为λ,第i个时间段所有航班的舱位个数为Ri,α为平均客座率,Ti为司机等待的第i批航班所消耗的时间,其中∑αRiλ+K0≥M+1,因此司机到达机场至回到市区的时间间隔为St0+∑Ti.其得到的收入为Q3=W-SL.
若司机选择放空返回,其与第一种情形的“放空”原理类似,因此,司机在该时间段的收益为
其中,k2指在“供过于求”放空返回市区状态下,在时间∑Ti+St0下,以90%的概率预估司机可能接到的乘客数.
利用上述式子可为司机设计选择策略,可得表1.

表1 供不应求的情况

表2 供过于求的情况
3.2 问题二模型的建立
3.2.1 当某一机场的相关数据及出租车数量可以获得的情况下,本文提出以下算法为出租车司机提供决策,并检验其合理性.
算法1:
输入:航班信息、乘客数量K0、排队等候的车辆M以及时间为星期A、t时段;
输出:“排队等待”或 “放空返回”;
具体步骤:
(i)如果K0≥M,转(ii),否则转(iii);
(ii)如果t属于早上5点~夜间23点,转(iv),否则转(v);
(iii)如果t属于夜间23点~早上5点,转(ix),否则转(x);
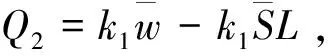
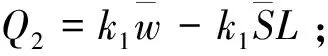
(vi)如果Q1>Q2,转(vii),否则转(viii);
(vii)选择“排队等候”策略更优;
(viii)选择“放空返回”策略更优;
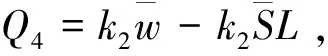
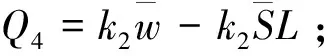
(xi)如果Q3≥Q4,转(xii),否则转(xiii);
(xii)选择“排队等候”策略更优;
(xiii)选择“放空返回”策略更优.
3.2.2 模型的合理性分析:
该模型是建立在问题一模型的基础上建立的,针对收集某一给定机场的相关信息以及当地出租车的相关数据对模型一进行了微调.该模型从实际的两种角度出发,分别在“供不应求”和“供过于求”的情况下出租车司机该如何抉择.两种情况都先分析如果出租车司机排队等候并载到了乘客时所花费的时间,再考虑若选择放空返回市区司机的收益情况,假定出租车司机无论是接到乘客还是放空返回所花费的时间是等同的,则只需考虑司机若将排队等候的时间用来在市区接载乘客,所获取的收益与之进行对比,在相同时间下对比收益具有一定的合理性,并且我们对现实分情况讨论,在不同情况先给出的选择建议也会随之发生改变.
对相关因素的依赖性.主要通过研究乘客数量的变化规律以及对比现已有乘客数与已正在排队等候的出租车数的数量关系,数量关系不同,选择方案也会不同.若在“供不应求”的情况下,则无需考虑后面的航班信息;若在“供过于求”情况下,还需知道后面的航班数量以及对客座率的估值,因为等待时间将会根据航班抵达情况被拉长.从机场到市区的时间也是一个重要因素,若放空返回,司机必然要承担空载油费的损失,但如果等待时间过长,在这段时间司机可通过在市区争取收益来弥补损失,该种情况下放空返回市区或许会成为更好的选择.
3.3 问题三模型的建立与分析[8]
蒙特卡洛模拟法[9],是一种通过设定随机变量的过程,反复利用某种分布的随机数生成时间序列,表示现实中可能出现的随机现象.又因每次实验只能代表一次可能出现的情况,所以,需要通过多次实验数从而获取有价值的统计结论.
蒙特卡洛模拟模型约束条件
① 乘客数量足够多,“乘车区”不会出现“车等人情况”;且“蓄车池”出租车数量足够多,不会出现乘客无车可坐情况;
② “乘车区”存在n个泊位,n位乘客同时上车;
③ “乘车区”每个乘客上车的时间均服从同一分布为y=f(x)=f(x1,x2,…);
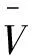
3.3.1 模型建立

其中C′表示并行车道通行能力(人/h),η表示每辆出租车平均载客人数,据了解,η一般等于1.4.
3.3.2 模型分析
重复操作上述模型,可得y个独立通行能力数值,分别记作C′i(i=1,2,…,y),取其平均数得
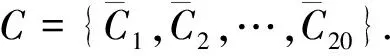
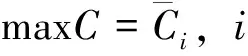
3.4 问题四的模型的建立与分析
3.4.1 模型的建立
基于排队模型的带优先服务权[10],非强占性优先权是指一个高优先级的出租车司机到达,也不能强制已经进入“乘车区”的低优先级出租车司机返回“蓄车池”.也就是说,一旦一名出租车司机开始进入“乘车区”载客,这项服务就不能被打断直至服务结束.
若出租车司机在将乘客送达目的地后迅速返回“蓄车池”后,根据出租车司机载客里程的长短拟对返回的司机赋予优先级,这里可以用司机往返时间长短来代表其载客里程长短.
从出租车司机搭载乘客离开“乘车区”开始计时,直至司机再次返回“蓄车池”截止计时,对出租车司机赋予N个优先级(其中,一级表示最高优先级),若同属于一个优先级内,则依据“先到先服务”原则.现假设某城市出租车司机载客往返时间为0 (v)当t>2T时,将其连同当日还未在机场接载过乘客的出租车司机一起划分为五级优先级(最低优先级). 并将“蓄车池”划分为5个车道,分别标号为1~5,相应级别优先级的出租车进入对应标号的“蓄车池”车道.同时,优先级别越高的车道距离“乘车区”越近,并且有优先进入“乘车区”载客的权利. 带优先权服务的[M/M/s]排队系统服务, 因此可知,这是一个[M/M/s]排队系统服务:表示出租车司机抵达蓄车池为泊松分布,在乘车区安排乘客上车时间为负指数分布,有s个乘车区. 为了体现该系统优先权对出租车司机排队等待模型的影响,对方案合理性进行检测.需要计算第k级优先级的出租车司机的平均等待时间(Wk,k=1,2,…,N)和平均队长(Lk,k=1,2,…,N).其中,Wk表示在稳定状态下k级优先级的出租车平均等待时间(包括在乘车区停留的时间),则非抢占性模型表示如下: 其中 Lk表示k级优先级在稳定状态下的平均队长(包括正在乘车区停车载客的出租车). 3.4.2 模型分析 根据上述模型的描述,可设计如下方案表及方案图: 表3 机场出租车优先级别划分表 通过查阅相关文献,发现2018年上海浦东机场飞机平均客座率为83.2%;再通过爬虫技术从携程网中获取该机场不同时间段抵达的航班号,接着从航空公司官网中查找对应航班的座位数. 据了解,上海浦东机场近两年抵达人数的比例是相对稳定的.白天乘客选择出租车的比例为15%,夜间为45%,该市出租车收费标准如下表所示: 表4 上海市出租车收费标准表 又知出租车司机油费L=0.6元/公里;站点最高发车率为10辆/分钟提高到30辆/分钟;机场到市区距离为48公里;市区限速为70公里/小时,高速限速为110公里/小时,为方便起见,可设司机开车的平均速率为90公里/小时.根据司机到达机场时机场现有乘客数、蓄车池中等待的出租车数量及时间,通过算法1,得司机决策方案如下: 表5 部分情况司机策略选择表 以上结果验证了本文所提模型的正确性和有效性. (i)依据泊松分布原理,以机场司机面临两种载客选择为背景,并以上海浦东国际机场为研究对象,分析研究“载客返市”“空车返市”两种决策下司机收益情况,通过建立排队论模型,利用Matlab为机场司机设计合理的决策方案.同时,为机场设计“X形立桥”并行车道提高乘车效率. (ii)通过分析机场普遍存在的出租车问题以及研究影响出租车司机选择决策的影响因素所建立的模型,对各个城市机场的出租车司机的策略选择均具有启发性作用,且具有较强的应用性;模型对一些不确定因素进行概率预测,通过比较较高概率下两个不同选择可能获得的收益时间,对出租车司机的选择提出合理建议;通过对出租车司机划分优先级以及通道来赋予某些出租车一定的“优先权”,既维护了司机的利益,又能维持现场秩序. (iii)存在的不足有不能将所有的影响决策因素纳入计算,依然存在统计偏差.但建立的模型方法简单易行,且易于应用于现实生活. 致谢作者非常感谢审稿人提出的宝贵意见以及相关文献对本文的启示.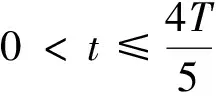
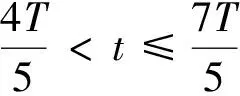

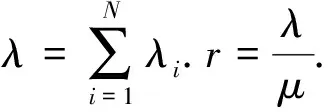

4 案例分析


5 结 论

