系数矩阵为行最简形的线性方程组的同解性

张姗梅， 刘耀军

(1.太原师范学院 数学系，山西 晋中 030619； 2.太原师范学院 计算机系，山西 晋中 030619)

1 引 言

线性方程组是线性代数的重要内容之一，主要涉及到线性方程组解的存在性、唯一性及其解法问题.这些问题在线性代数中已经得到了比较充分的讨论.但在教学过程中，学生常常提问，两个线性方程组同解的条件是什么？

这个问题在现行教材中没有完整的论述，为了回答这个问题，国内学者进行了深入的讨论.在文献[1]中，利用向量组的极大无关组，证明了两个线性方程组同解的充要条件是它们的增广矩阵的行向量组等价；在文献[2]中，利用[1]的结论，给出了两个线性方程组同解的充要条件的秩的刻画；在文献[3]中，利用线性方程组解的存在性定理和[1]的结论，得到两个线性方程组同解的充要条件是它们对应的齐次线性方程组同解，但是这个结论的充分条件是错的；在文献[4]中，利用线性方程组的解的结构定理，纠正了[3]中的错误，指出两个线性方程组同解的充要条件除了它们对应的齐次线性方程组同解之外，还应该附加条件“两个方程组有公共解”.

按照从简单到复杂的认知规律，从最简单的线性方程组——系数矩阵为行最简形矩阵的线性方程组入手，讨论线性方程组的同解性.利用矩阵的秩的概念，通过讨论由两个同解方程组合并而成的辅助方程组，证明了同型的系数矩阵为行最简形的线性方程组同解的充要条件是他们的增广矩阵相等；利用这个结论，得到一般的线性方程组同解的结论，证明了矩阵的行最简形矩阵的唯一性.与传统的线性相关性方法[1-4]比较，这里的方法是构造性的.因为系数矩阵为行最简形的线性方程组足够简单，使得同解性问题可以通过直接计算得到解决，也使得“矩阵的行最简形矩阵的唯一性的证明”比主元列法的证明[5-8]更加清晰.

在文中，m，n是正整数，x=(xi)n×1是未知量向量，In是n阶单位阵，R(A)是矩阵A的秩.

2 系数矩阵为行最简形的同型齐次线性方程组的同解性

解系数矩阵为行最简形的齐次线性方程组只需要移项，因此系数矩阵为行最简形的齐次线性方程组是最简单的线性方程组，其性质更容易证明.

定理1系数矩阵为行最简形的同型齐次线性方程组的同解性.设C与D是m×n行最简形矩阵.如果Cx=0与Dx=0同解，那么C=D.

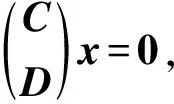
当r=0时，由R(C)=R(D)=0知，C=D=O.对于r≥1的情形，分两步证明C=D.第一步，利用数学归纳法证明C与D的每个非零行的首1元素所在列的位置相同；第二步，通过解线性方程组证明C与D的对应元素相等.

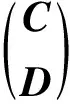
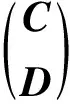
xji=-cij(1≤i≤r)，xj=1，xk=0 (k∈{1，2，…，n}-{j1，j2，…，jr，j}).

因为方程组Cx=0和方程组Dx=0同解，所以它也是Dx=0的解，将此解代入Dx=0的第i个方程，得恒等式-cij+dij=0，故cij=dij.因此，C=D.

3 系数矩阵为行最简形的同型非齐次线性方程组的同解性

线性方程组和它对应的齐次线性方程组的解之间有如下关系：线性方程组两个解的差是其对应的齐次线性方程组的解；非齐次线性方程组的一个解与其对应的齐次线性方程组的解的和是非齐次线性方程组的解.借助这些性质，可得两个线性方程组同解与其对应的齐次线性方程组同解的关系.

引理1[3]设A与B是m×n矩阵，a与b是m维常数列向量.如果Ax=a与Bx=b有解并且同解，那么Ax=0与Bx=0同解.

利用系数矩阵为行最简形的齐次线性方程组同解的结果，作为定理1的应用，可以得到系数矩阵为行最简形的非齐次线性方程组同解的增广矩阵的关系.

定理2系数矩阵为行最简形的同型非齐次线性方程组的同解性.设C与D是m×n行最简形矩阵，c=(ci)m×1与d=(di)m×1是常数列向量.如果Cx=c与Dx=d有解并且同解，那么

(C|c)=(D|d).

证因为Cx=c与Dx=d有解并且同解，所以由引理1知，Cx=0与Dx=0同解，再由定理1得C=D.设R(C)=r，C如定理1证明所述.当r=0时，由R(C)=0知，C=D=O，因为Cx=c与Dx=d有解，所以(C|c)=(D|d)=0.对于r≥1的情形，下面证明c=d，为此解线性方程组Cx=c，把非零行的首1元素对应的未知量保留在方程左边，其余项移到方程右边，得方程组Cx=c的解.

所以ci=di=0(n

当r

xji=ci(1≤i≤r)，xj=0(j∈{1，2，…，n}-{j1，j2，…，jr}).

因为Cx=c与Dx=d同解，所以，它也是Dx=d的解，将此解代入Dx=d的第i(1≤i≤r)个方程中得到ci=di.因为Cx=c与Dx=d有解，所以

R(C|c)=R(D|d)=r，

这样对于r

例如，如果

和

有解且同解，那么由两个方程组的第二个方程可见c2=d2=0.第一个方程组的解为x1=c1-ax2，由此x2=0，x1=c1是第一个方程组的一个解，因为两个方程组同解，所以x2=0，x1=c1是第二个方程组的解，代入第二个方程组的第一个方程中得c1=d1；x2=1，x1=c1-a是第一个方程组的解，代入第二个方程组的第一个方程得c1-a=d1-b，因此a=b.于是

4 应 用

由高斯消元法知，一般线性方程组的问题可以化为系数矩阵为行最简形矩阵的线性方程组讨论.

4.1 同型齐次线性方程组的同解性

对于齐次线性方程组，通过矩阵的初等行变换，把方程组的系数矩阵化为行最简形矩阵，解此系数矩阵为行最简形的齐次线性方程组得到原齐次线性方程组的解.因此，此系数矩阵为行最简形的线性方程组蕴含原方程组的信息.借助定理1可得到同解的齐次线性方程组的系数矩阵间的关系.

推论1设A与B是m×n矩阵，如果Ax=0与Bx=0同解，那么A与B是行等价的.

证设A通过初等行变换化为行最简形矩阵C，则A与C行等价，Ax=0与Cx=0同解；设B通过初等行变换化为行最简形矩阵D，则B与D行等价，Bx=0与Dx=0同解；如果Ax=0与Bx=0同解，那么Cx=0与Dx=0同解.由定理1知C=D，从而由行等价的对称性和传递性知A与B是行等价的.

高斯消元法表明，如果A与B行等价，那么Ax=0与Bx=0同解.推论1指出其逆命题也成立.因此，Ax=0与Bx=0同解的充分必要条件是A与B行等价.

4.2 矩阵的行最简形矩阵唯一性的证明

根据系数矩阵行等价的齐次线性方程组同解，借助定理1可证矩阵的行最简形矩阵的唯一性.

推论2矩阵的行最简形矩阵唯一.

证设A是m×n矩阵，C与D都是A的行最简形矩阵，则齐次线性方程组Ax=0与Cx=0和Dx=0同解.由Cx=0与Dx=0同解，C与D都是行最简形矩阵，根据定理1得C=D.

4.3 同型非齐次线性方程组的同解性

通过线性方程组与系数矩阵为行最简形的线性方程组的联系，借助定理2，可得同解线性方程组的增广矩阵间的关系.

推论3设A与B是m×n矩阵，a与b是m维常数列向量.如果Ax=a与Bx=b有解并且同解，那么(A|a)与(B|b)是行等价的.

证设(A|a)通过初等行变换化为行最简形矩阵(C|c)，则(A|a)与(C|c)行等价，Ax=a与Cx=c同解；设(B|b)通过初等行变换化为行最简形矩阵(D|d)，则(B|b)与(D|d)行等价，Bx=b与Dx=d同解；如果Ax=a与Bx=b有解并且同解，那么Cx=c与Dx=d有解并且同解.由定理2知(C|c)=(D|d)，从而由行等价的对称性和传递性知(A|a)与(B|b)是行等价的.

高斯消元法表明，如果(A|a)与(B|b)行等价，那么Ax=a与Bx=b同解.因此，如果Ax=a与Bx=b有解，那么Ax=a与Bx=b同解的充分必要条件是(A|a)与(B|b)行等价.

4.4 任意线性方程组的同解性

因为在线性方程组中添加方程0=0不改变方程组的解，在矩阵中减少0行不改变行向量组的等价性，因此由推论3可得如下推论.

推论4任意两个线性方程组有解并且同解的充要条件是它们的增广矩阵的行向量组等价.

4.5 主元列的唯一性

辅助方程组方法将两个矩阵联系在了一起，为比较两个行最简形矩阵带来方便.辅助方程组方法也可用于行阶梯形矩阵的比较.用辅助方程组方法可以证明：

推论5与一个矩阵行等价的任意两个行阶梯形矩阵的对应非零行的首非零元素所在列的位置都相同.

事实上，设C与D都是与m×n矩阵A行等价的行阶梯形矩阵，则方程组

Ax=0，Cx=0，Dx=0

同解.从而

同解，于是

把定理1证明“C与D的每个非零行的首1元素所在列的位置相同”的证明稍作修改，就可以证明C与D的对应非零行的首非零元素所在列的位置都相同.

5 结 论

本文主要探讨了系数矩阵为行最简形矩阵的线性方程组的同解性，并由此证明了线性方程组同解的充要条件和矩阵行最简形矩阵的唯一性.得到的结论丰富了线性代数教材的内容，对教学具有一定的参考价值.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.