和式极限的一致等价替换定理

王德荣， 黄永忠， 邵 琨

(华中科技大学 数学与统计学院，武汉 430074)

1 引 言

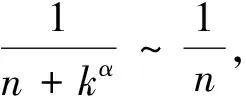
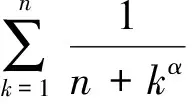
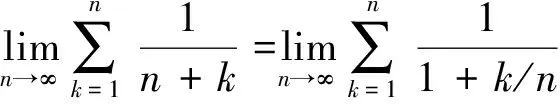
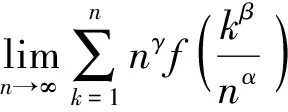
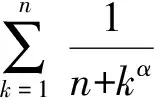
2 和式极限的相关定理及应用

|βkn/αkn-1|<ε(k=1，2，…，n)，

则称αkn与βkn在n→∞时关于k=1，2，…，n为一致等价的.简称αkn与βkn关于k一致等价，也称αkn的一致等价量为βkn.

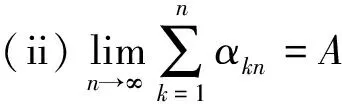
由定义1可直接得到以下两个引理，用于判别一致等价性.

定理2若f(x)在[0，1)上有m阶导数，且

f(0)=f′(0)=…=f(m-1)(0)=0，f(m)(0)=c≠0，

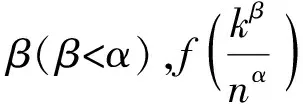
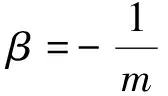
证x∈(0,1)时，利用Taylor公式

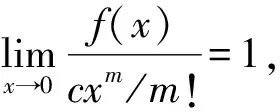
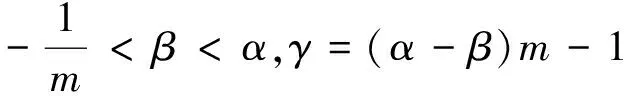
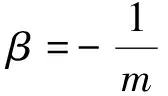
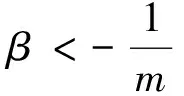
注 参考文献[3-4]中仅考虑到α,β为正整数的情形，定理2给出的是更一般的结论.

例1计算以下和式极限.

解(i)令f(x)=x-sinx，则

f(0)=f′(0)=f″(0)=0，f‴(0)=1，

因此

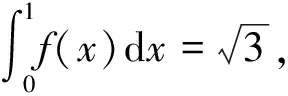
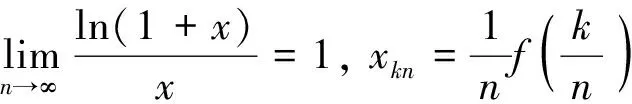
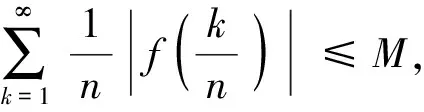
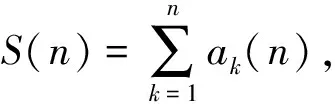
应用定理1与定理3计算以下极限.

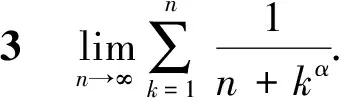
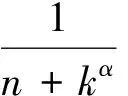
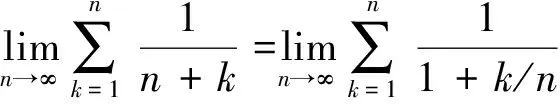
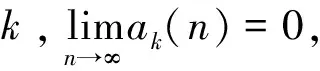
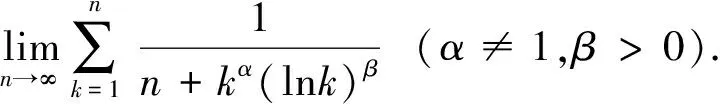
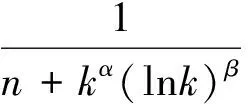
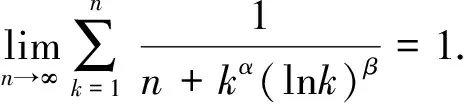
钱泰吉(1791—1863)《曝书杂记》：“余昔有明初抄本，即《解题》所载本”。可见宋末新出现的这个本子在明初尚有钞本，且至少流传到清钱泰吉(1791—1863)之世。

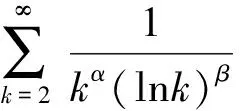
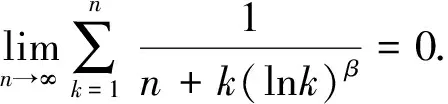
3 和式极限的收敛阶

以下以命题的形式给出一些和式极限的收敛阶.

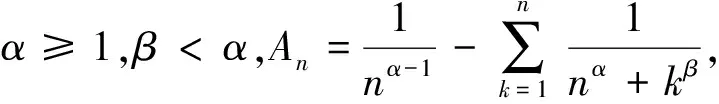
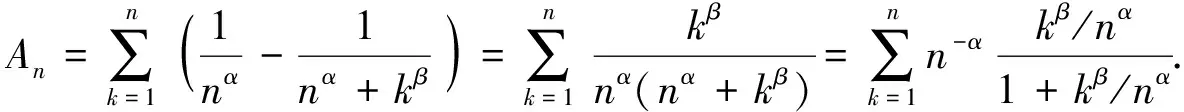
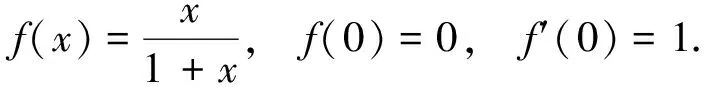
(i)若β>-1，

(ii)若β=-1，

(iii)若β<-1，

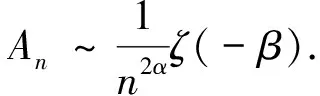
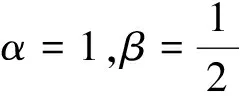
当α>-1时，

利用定理1可得

而α=-1时，

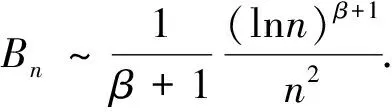
3 结 论

给出了求和式极限的一致等价替换原理，得到了极限

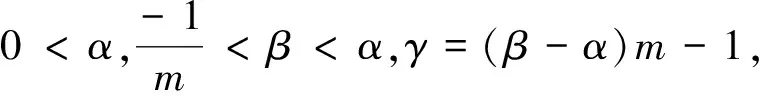
致谢作者非常感谢参考文献[2-4]对本文的启发以及审稿专家提出的宝贵意见.