具有4阶核矩阵极化码的构造和译码研究

马奎明,李文慧,李秀丽

(青岛科技大学 数理学院,山东 青岛 266061)

香农(Shannon)指出:任何一个通信信道都有确定的信道容量C,如果通信系统所要求的传输速率R＜C,则存在一种编码方法,当码长N足够大时,应用最大似然译码MLD(maximum likelihood decoding),信息的错误概率可以达到任意小[1]。这就是著名的有噪信道编码定理,它奠定了纠错编码理论的基石。然而它没有给出如何构造实际上可实现的、具有上述性能的这类码。这正是信道编码要解决的问题。信道编码的目的是寻找实际中易于实现且能达到有效而可靠通信的编译码方法。

在过去的50年里,编译码学家们提出了多种校验纠错码技术,例如RS码、卷积码,Turbo码等,并广泛地使用到各种通信系统中。然而,所有的编码方法都不能达到香农极限(也称为香农边界)。2008年,在国际信息理论会议(ISIT)上,土耳其毕尔肯大学埃达尔.阿利坎(Erdal ARIKAN)教授首次提出了信道极化的概念。在这一理论的基础上,他给出了第一种已知能够被严格证明能够达到任意对称二进制输入离散无记忆信道(BI-DMC)信道容量的新型编码方式,并命名为极化码(polar code)。

极化码具有明确且简单的编码和译码算法,其主要的思想是信道分裂和信道组合,经过信道的组合和拆分可将N个独立的,有相同参数的信道变成N个具有相关性且信道容量分布发生变化的信道,信道总容量保持不变[2]。信道容量发生极化:一部分信道容量增大,一部分信道容量减小。这给信道编码提供了很好的理论基础依据。

不同的核矩阵会导致不同的性能,而核矩阵阶数越高,所构造的极化码块长度也越大,实现信道极化的程度更彻底,性能更好,因此如何构造具有高阶核矩阵的极化码是一个非常具有研究意义和实用性的课题。本研究对于一般情况,以偏序法为例,详细阐述了具有4阶核矩阵的极化码构造原理和过程,并采用串行相消译码器,对其译码过程进行了讨论。最后,对极化码潜在的研究方向、意义和可能遇到的困难点进行了总结。

1 信道极化

1.1 基本原理

极化码主要研究的是二进制离散无记忆信道(B-DMC),也主要对二进制离散无记忆信道说明其基本的极化原理。用X、Y分别代表B-DMC信道W的输入和输出符号集,X∈{0,1},W的传输概率是W(y|x),x∈X,y∈Y。当输入符号X等概率的取{0,1}时,它的对称信道容量,可表示为

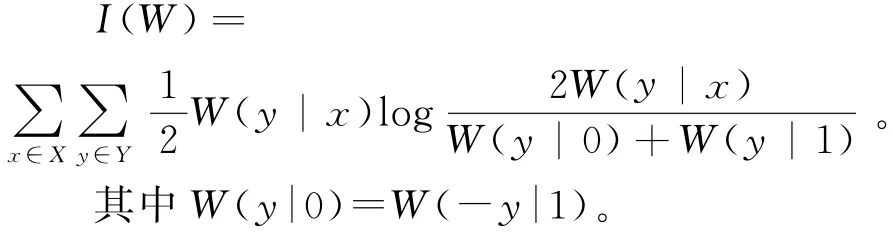
信道容量是指信道能够传输的最大信息量,它仅由信道自身的性质决定,与信源和信宿无关。在信道编码领域中,信道容量是一个非常重要的研究量。从信道容量的定义式中可以看出,只要信道的传输概率确定了,那么信道容量也就确定了[2]。

极化码是根据子信道的信道容量大小进行编码构造的。通过信道变换导致部分子信道信道容量发生改变,从而容量大的信道传输包含信息的信息比特,容量小的信道传输发收端均已知的固定比特,这就是极化思想。它充分利用了信道变换这一特点,实现了信道极化,再根据信道变换结构的特点构造出相应的编码方案,从而得到一种复杂度低的、质量高的信道编码方案。

1.2 信道的组合和分裂

信道组合就是将B-DMCW递归操作组合起来形成W N,其中N＝2n,n≥0。当n＝0时,信道复制一次,W1＝W。当n＝1时,复制的信道进行组合得到信道W2,如图1所示。

图1 W 2的信道组合Fig.1 Channel combination of W 2

当n＝2时,信道进行组合得到W4,如图2所示。

图2 W 4的信道组合Fig.2 Channel combination of W 4

当n＝3时,信道进行组合得到W8,如图3所示。

图3 W 8的信道组合Fig.3 Channel combination of W 8

以此类推,可以得到n＝n－1时,组合信道W N,如图4所示。

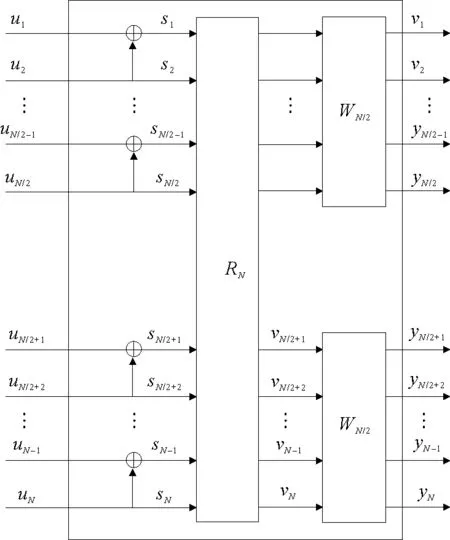
图4 W N的信道组合Fig.4 Channel combination of W N

对输入序列u进行线性变换后可得到编码序列x,其变换操作可用生成矩阵GN来表示

此时信道的传输概率为

信道分裂是信道组合的逆过程,将组合信道W N再拆成N个二进制输入信道W(i)N,其对应的转换概率为

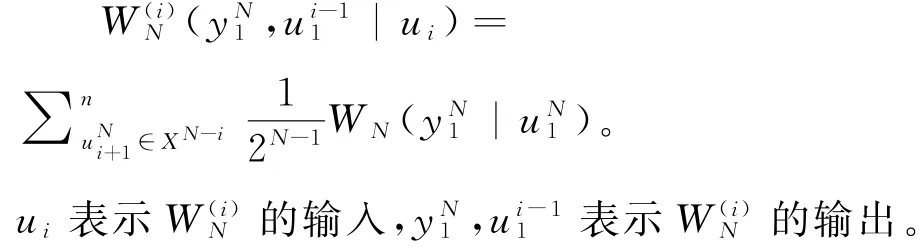
2 偏序构造法

满足标准的4阶核矩阵不止一个,例如

定义1[5]设R是集合A上的一个二元关系,若R满足:

(1)自反性:对任意x∈A,有xRx。

(2)反对称性:对任意x,y∈A,若xRy,且yRx,则x＝y。

(3)传递性:对任意x,y,z∈A,若xRy,且yRz,则x＝y。

则称R是A上的偏序关系。

偏序法的研究基于以下结论:如果j是通过在i的二进制扩展中将较高的1与较低的0交换而获得的,则W N(j)随机退化为W N(i)。

定义2[5]设W1,W2分别为相同的二进制输入信道X1→Y1,X2→Y2。如果概率分布p(y1|y2)存在

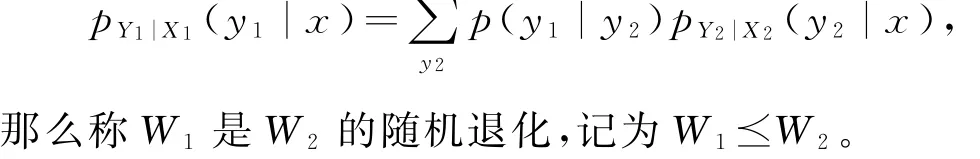
在m个字母上的排列是Zm到自身的双射。在m个字母上的排列π的置换矩阵是元素在{0,1}中唯一满足以下条件的m×m矩阵P。

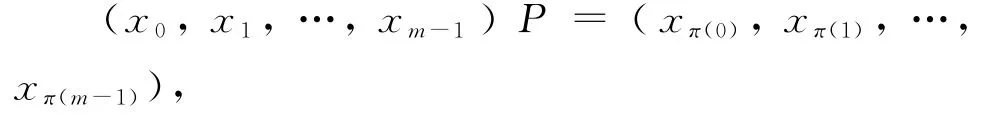
对所有矢量x,都有

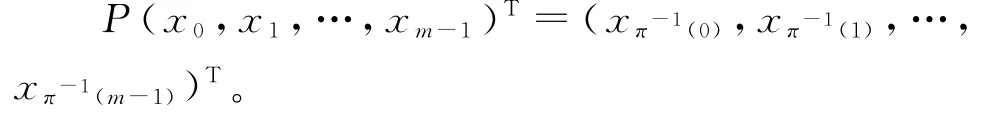
定义3设π是m个字母的排列。对2m个字母的排列sπ称为位显著排列。

其被定义为k→k′的映射,其中k′是l进制(l≥2)的整数,表示为

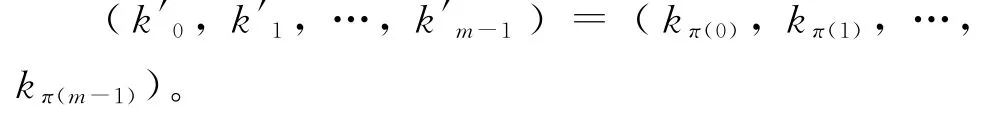
这里k0,k1,…,km－1表示k的l进制。

BN表示N个字母的位反转排列矩阵[6]。Gl为l×l阶二进制非上三角矩阵。设GN＝BNG⊗nl,其中⊗运算是二进制域GF(2)上的克罗内克积。

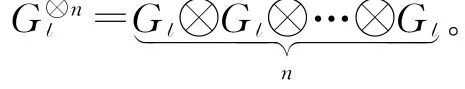
设信道Xi→Yi,i∈ZN是独立且均匀分布二进制输入信道W。定义[3]

块长度N趋于无限大时,无噪信道的比例接近I(W),全噪信道的比例接近1－I(W)[7]。

推论2记GN＝QGNP－1,其中P是任意N×N阶位显著排列矩阵,Q＝BNPB－1N是一个置换矩阵。

定义4[8]令i,j∈ZN,sπ是N个字母上的位显著排列。如果满足

表1 i和sπ(i)对应关系Table 1 i and sπ(i)corresponding relationship

证明在评估作为ML译码[9]在子信道W(i)N上的错误概率P(W(i)N)时,因为信道W是对称的,则假设所有零信息都会被传输。设a(i)N表示传输所有的零信息时,logL(i)N(yN－10,0i0)的概率密度函数。计算密度的规则如下:

这里a(0)＝aW是发送0时,原始信道W的的概率密度函数,*和◦是在可变节点域和校验节点域上的卷积运算。

定理1[10]偏序有3个重要的性质:

1)嵌套:码长为N,xy意味着在码长为4N中,xy也成立。

2)乘法:码长为N,xy意味着当码长为4N,(4x＋i)(4y＋i)成立,i＝0,1,2,3

3)对称性:xy和N－1－xN－1－y是块长为N的极化码的一对

证明 嵌套的性质很容易证明。因为长度为N＝4n的4进制(xn－1…x1x0)4表示为长度为4N的(0xn－1…x1x0)4,这并不影响1和2。

证明乘法性质,设N＝4n,x和y的4进制表示分别为(xn－1…x1x0)4和(yn－1…y1y0)4。如果x1y,那么存在某些t∈Zn,当k∈Zn,t≠k时,xt＜yt且xk＝yk。则4x＝(xn－1…x1x00)4,4y＝(yn－1…y1y00)4。明显,当块长为4N时,4x14y。同样的,当块长为4N,有4x＋14y＋1,4x＋24y＋2和4x＋34y＋3。对于2,同样成立。

3 译 码

Arikan采用串行对消译码器对极化码进行译码。将在本节介绍具有4阶核矩阵的极化码的译码原理及过程。

这样,单个长度为N的信道的似然比(LR)[4]的计算就简化为4个长度为N/4的信道的似然比的计算。这个递归可以应用到块长为1的信道,此时似然比的形式为

它是可以直接计算的,那么需要计算的似然比总数为N(1＋lgN)。

4 结 语

从代数编码和概率编码的角度来说,极化码具备了两者独有的特点。首先,只要给定编码长度,极化码的编译码结构就唯一确定了,而且可以通过生成矩阵的形式完成编码过程,这一点和代数编码的常见思维是一致的。其次,极化码在设计时并没有考虑最小距离特性,而是利用了信道组合(channel combination)与信道分裂(channel splitting)的过程来选择具体的编码方案,而且在译码时也是采用概率算法,这一点比较符合概率编码的思想。

偏序法是一种简单直观的方法,但由于其本身就是乱序的,因此不能对信道进行完全的排序。其它的构造方法也各有优劣,例如:密度演化方法可以对信道进行完整的排序,但计算量大,计算复杂;广义极化权重法可以对信道进行完全的分类,但是不同类型的信道需要确定不同的β;高斯近似方法可以对信道进行完全排序,并且具有与Arikan启发式方法相同的复杂度,相对来说性能有所提高,但只适用于高斯白噪声信道(AWGN)。

除此之外,极化码想要得到更多应用还要克服高速率通信下的时延和吞吐率[11]问题,这是极化码在应用上最大的问题。