基于智能PD型迭代学习控制的清扫车路径跟踪控制

姚文龙,庞 震,池荣虎,邵 巍,王华东

(青岛科技大学a.自动化与电子工程学院;b.信息科学技术学院,山东 青岛 266061)

路径跟踪技术在机器人控制、无人驾驶车控制、无人机控制、机械臂跟踪控制等领域有着广阔的应用前景[1-4]。其中,无人驾驶车技术除了在传统家用汽车应用较广之外,也逐渐应用在开采环境勘探、农业生产、园区道路清扫等多个领域[5-6]。园区清扫车利用清扫场地固定的特点,工作模式一般是设定清扫路线,定期自动循环清扫、洒水,减轻了环卫压力。其中,自动导航技术是园区清扫车自动化运行的关键技术,主要包括环境感知、路径规划和路径跟踪三方面的研究内容[7]。本研究主要对园区道路清扫车的路径跟踪技术展开研究。

在实际研究中,清扫车的跟踪路径与时间呈现复杂的非线性关系,车辆系统本身也是复杂难建模的非线性系统,因此,控制器的设计较为困难[8]。目前大多应用两轮或四轮的移动机器人代替智能车辆展开研究[9-10],园区清扫车路径跟踪实际上就是智能移动机器人的路径跟踪,即是指根据给定的期望路径,自主调整前轮转向,使稳定跟踪到期望路径。叶长龙等[11]基于4组并联布置MY轮全方位移动平台和2自由度并联举升机组成的5自由度全方位移动机器人,设计双曲线滤波PD控制器进行路径跟踪仿真,跟踪误差随跟踪时间减小而减小;刘美珍等[12]基于非完整轮式移动机器人运动学模性,设计路径跟踪的虚拟速度控制量,得到系统的持续激励输出,同时根据动力学模型推导系统的不确定项,采用高度非线性拟合特性的神经网络对其进行估计,得到模型力矩控制量,组成复合控制策略,提高控制精度;葛媛媛等[13]建立不确定非线性移动机器人运动学模型,基于光滑非线性饱和函数,建立自适应模糊滑模控制器,并利用界定有界输入有界输出,保证系统稳定收敛;宋立业等[14]利用Lyapunov函数设计了运动学控制器,并采用反演方法和积分滑模控制设计自适应神经滑模动力学控制器,调节系统的控制参数,提高了跟踪精度。

上述方法都是在时间域上进行控制系统设计,然而,在园区清扫车实际工作中,主要在固定路段周期性重复进行清扫、洒水等工作,具有很强的重复性特点,对于循环运行中的有效信息没有充分利用。此外,随着清扫垃圾的不断增多,车身重量发生实时变化,由此带来非重复不确定性扰动,使得控制系统的收敛速度和鲁棒性都受影响。基于以上考虑,本工作提出利用迭代学习方法对园区清扫车路径跟踪控制展开研究,首先,将含非线性不确定项的清扫车非线性系统转化为线性仿射数据模型;利用循环工作过程中得到的跟踪误差与控制输入信号,采用迭代差分估计算法估计非线性不确定项,并设计基于投影算法的参数更新率,引入非重复时变扰动的比例项和微分项,得到基于智能PD迭代学习控制算法的路径跟踪控制器,实现对未知扰动的有效估计,提高控制系统收敛速度、增强控制算法对非重复时变扰动的鲁棒性。最后,仿真验证方法的可行性。

1 问题描述

1.1 车辆运动学模型建立

动力学模型和运动学模型是车辆模型建立过程中最常用的两种模型[15-16],动力学模型要根据车辆在行驶过程中的受力情况,利用牛顿第二定律建立,但对于园区清扫车,随着清扫垃圾的增多,车身重量不断变化,无法建立精确的动力学模型;运动学模型是从空间几何的角度研究车辆的运动规律,包含车辆位置、航向角等参量,能够提供系统的输入输出数据,同时显示了系统的非线性特征。园区清扫车一般低速行驶,可以忽略行驶中侧滑等动力学问题[17],因此采用运动学模型研究园区清扫车的路径跟踪问题。

目前,园区清扫车多为四轮电驱动车辆,双前轮控制车辆的转向,双后轮驱动车辆行驶,本工作主要研究的是车辆的转向控制,设计的控制系统输出控制车辆的前轮转动。首先,给出车辆的运动学模型,如图1所示。

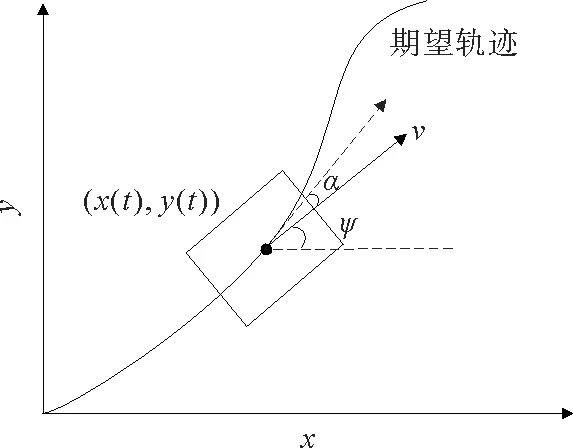
图1 园区清扫车路径跟踪运动学模型Fig.1 Kinematic model of track tracking of park sweeping car

在清扫车运动学模型研究中,考虑清扫车为一个整体,忽略车身长度影响,取(x(t),y(t))为清扫车的中心点位置;ψ为清扫车行驶方向与坐标横方向的夹角,即清扫车的航向角;α为清扫车的前轮转角,即转向控制器输出控制量,由图1可知,车辆中心位置的运行速度为

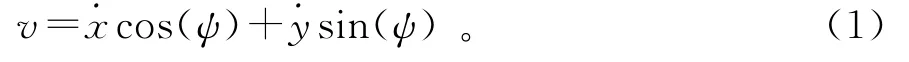
运动学约束方程为

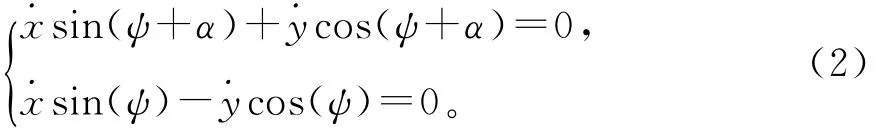
由式(1)和式(2)可得

车辆的横摆角速度w为

由式(4)得到清扫车的运动学模型:

1.2 系统线性化

由式(3)可以看出,前轮转角控制系统是与之前车辆航向角和前轮偏转角相关的非线性系统,可以等效表示为

其中,ψ(k,i)和u(k,i)分别为系统的输出和输入;k为系统的迭代循环次数,且k∈N*;i为系统的运行时间,且i＞0;f(…)为未知非线性函数;nψ,nu为正整数。

针对园区清扫车运动学模型,提出如下几点假设:

假设1受车辆前轮最大偏转角限制,非线性函数f(…)对于有界自变量是有界的。

假设2根据车轮横摆角速度限制,非线性函数f(…)对控制输入u(k,i)的偏导数是连续有界的,且偏导数的符号已知不变。

假设3式(4)所示非线性系统满足广义Lipschitz条件,即:当Δu(k,i)≠0,b＞0,存在:

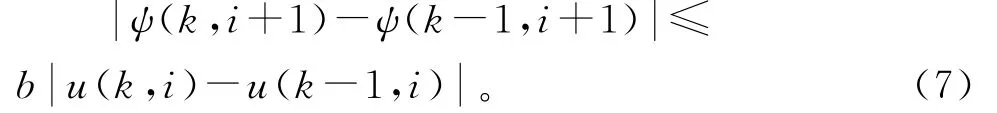
当系统满足上述假设1～3时,可将式(6)转化为如下紧格式局部线性化数据模型:

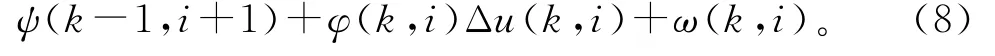
其中,φ(k,i)＝∂f*/∂u(k,i);

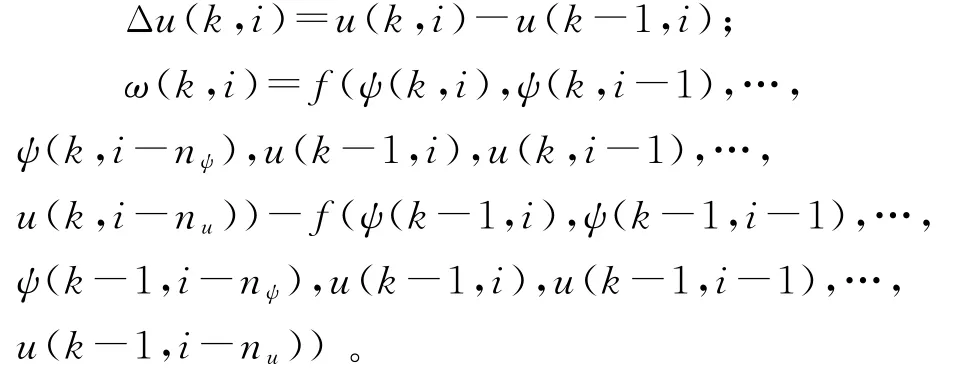
上述模型仅需要输入输出数据,不仅考虑了额外的误差信息,还加入非线性不确定项作为补偿,消除清扫车转向控制中的实时变化的不确定扰动影响,需要对其进行估计。

2 控制器设计

根据上述式(8)得到的紧格式局部线性化数据模型,由等价反馈原理得到

其中,λ＞0为权重因子。

为提高控制器的鲁棒性,设计智能PD型迭代学习控制方案,在上述控制算法中加入误差反馈项,其中跟踪误差为e(k,i＋1)＝ψd(k,i＋1)－ψ(k,i＋1),得到控制算法为

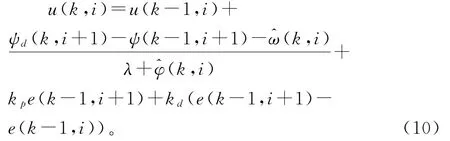
其中,kp,kd是学习增益。

在上述控制算法中,^ω(k,i),^φ(k,i)为ω(k,i),φ(k,i)的估计值,需要设计参数估计算法对其进行估计。

对于φ(k,i),给出如下估计准则:

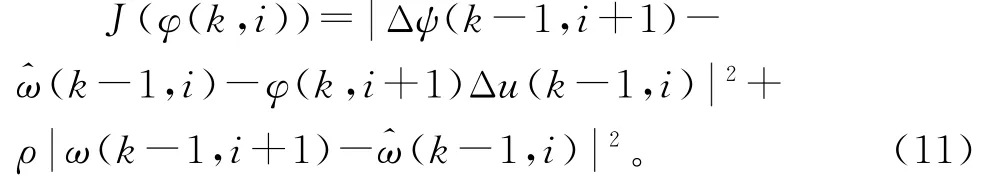
将式(8)代入式(11)中,两边对φ(k,i)求偏导,并令∂J/φ(k,i)＝0,得到φ(k,i)的估计值:

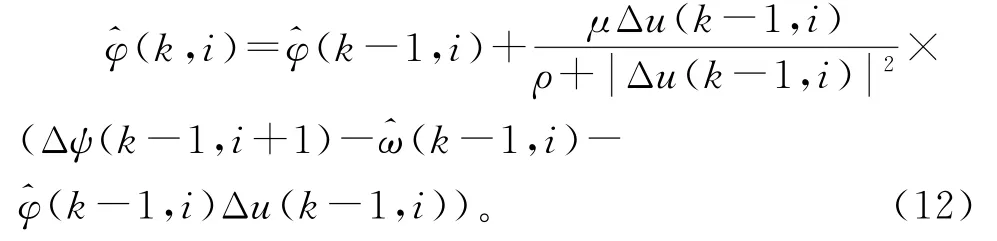
其中,ρ＞0为权重因子;μ∈(0,1]为步长因子。

ω(k,i)为未知非线性不确定项,利用时间差分估计算法对其进行估计,如下:

综上,基于紧格式局部线性化的智能PD型迭代学习控制方案如下:

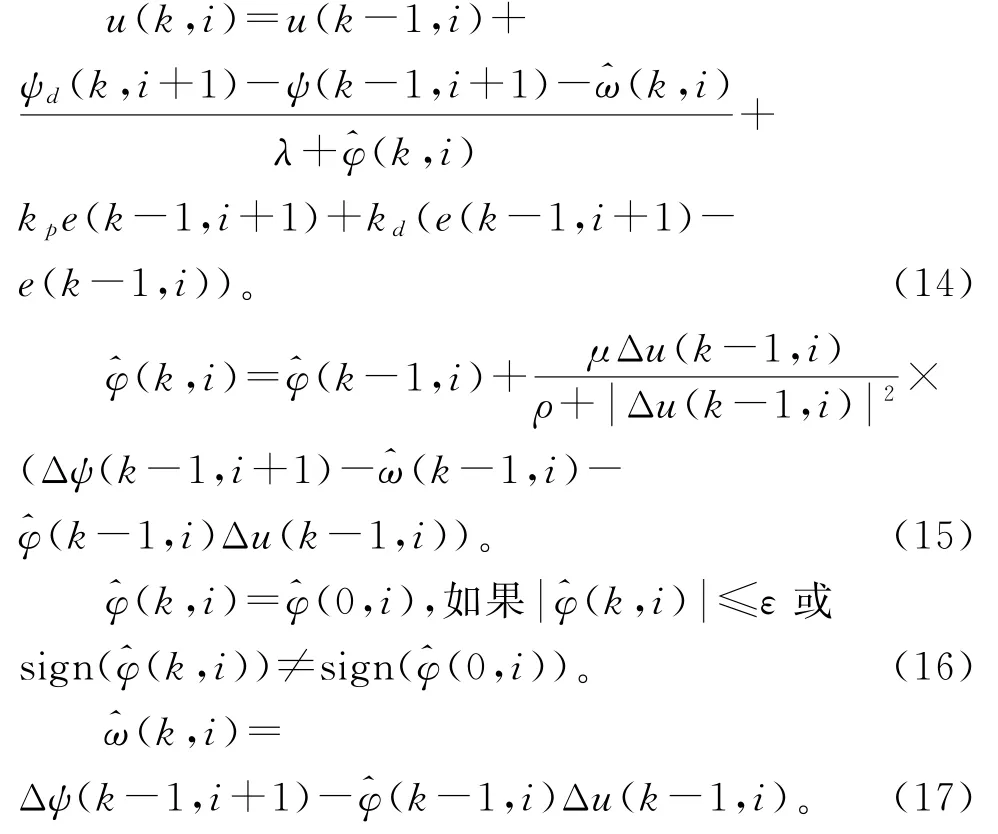
其中,^φ(0,i)为^φ(k,i)的迭代初值;ε＞0为一个极小的正值。

3 仿真分析

实际应用中,根据园区清扫车工作环境,主要由直线路径和曲线路径组成,本仿真主要针对直线路径跟踪和曲线路径跟踪展开研究,若上述控制器设计方法可以取得较好效果,那么对于实际应用中智能清扫车道路清扫工作的路径跟踪也是有效的。

3.1 直线路径跟踪仿真分析

假设清扫车的路径跟踪期望航向角为

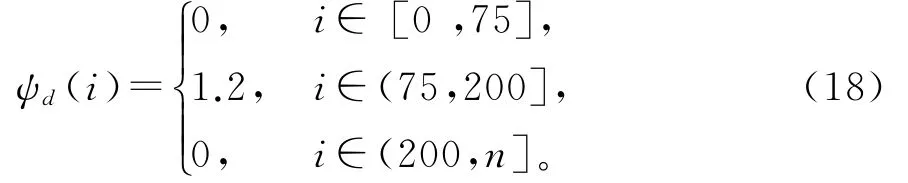
其中,车辆的期望初始航向角为0,期望初始位置为(0,0),因此,仿真中,将跟踪的初始条件设为ψ(k,0)＝0,(x(k,0),y(k,0))＝(0,0),第一次迭代时的控制输入u(0,i)＝0,在系统中加入非重复扰动,仿真时间n取500,控制器的参数主要包括:ρ＝0.8,μ＝0.9,η＝0.4,kp＝0.1,kd＝0.5,仿真结果如图2和图3所示,分别为不同迭代次数下直线路径跟踪的航向角-时间曲线和位置路径跟踪曲线。

由图2可以看出,随着迭代次数的增加,车辆航向角与期望航向角之间的误差不断减小,在经过10次迭代后,清扫车可以较好的跟踪直线路径的期望航线角变化,且扰动影响下,仍稳定跟踪。图3为不同迭代次数下的车辆位置路径跟踪曲线,通过对比可以看出:在2次、3次、5次迭代时,车辆位置与期望跟踪路线坐标误差不断减小,在10次迭代时,跟踪误差逐渐趋于0,实现了高精度的位置路径跟踪,且扰动影响下,未出现明显偏差,具有较强鲁棒性。

图2 不同迭代次数下的航向角-时间曲线Fig.2 Course angle-time curve under different iteration times

图3 不同迭代次数下的车辆直线路径跟踪位置曲线Fig.3 Vehicle linear trajectory tracking position curve under different iteration times

3.2 曲线路径跟踪仿真分析

假设清扫车的路径跟踪期望航向角为

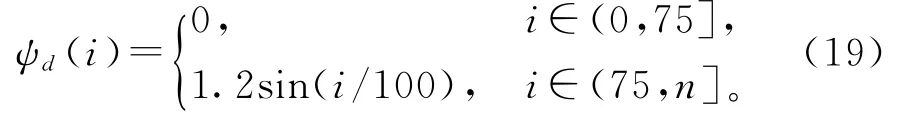
在曲线跟踪时,采用与直线跟踪时相同的初始条件、控制算法及参数,车辆的期望初始航向角为0,期望初始位置为(0,0),因此,仿真中,将跟踪的初始条件设为ψ(k,0)＝0,(x(k,0),y(k,0))＝(0,0),第一次迭代时的控制输入u(0,i)＝0,系统中加入非重复扰动仿真时间n取550,选用与直线路径跟踪时相同的控制器参数,仿真结果如图4和图5所示,分别为不同迭代次数下曲线路径跟踪的航向角-时间曲线和位置路径跟踪曲线。

由图4可以看出,经过不断迭代,曲线路径航向角的跟踪误差不断减小,在10次迭代时,基本可以较好的跟踪车辆期望航向角曲线,且扰动影响下,仍稳定跟踪;图5为不同迭代次数下的车辆位置估计跟踪曲线,通过对比可以看出:在2次、3次、5次迭代时,车辆位置与期望位置跟踪误差不断减小,在10次迭代时,跟踪误差逐渐趋于0,系统是收敛的,且扰动影响下,未出现明显偏差,具有较强的鲁棒性。

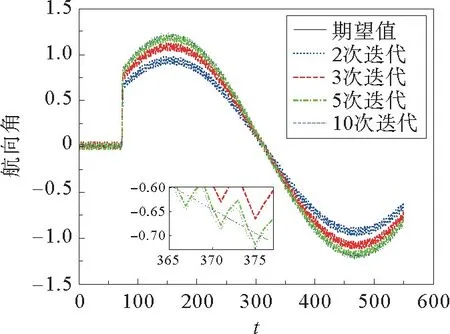
图4 不同迭代次数下的航向角-时间曲线Fig.4 Course angle-time curve under different iteration times

图5 不同迭代次数下的车辆曲线路径跟踪位置曲线Fig.5 Vehicle curve trajectory tracking position curve under different iteration times

两种期望路径的跟踪仿真基本可以涵盖园区清扫车实际应用中的行驶路径,仿真分析说明,迭代学习控制可以较好的利用清扫车循环运行的信息,并且利用智能PD型迭代学习控制算法,提高了路径跟踪精度,可达到无偏差跟踪,满足路径跟踪的高精度要求。

4 结 语

园区清扫车主要是在园区固定路段周期性地循环清扫工作,具有很高的重复性特点,利用循环运行中的重复性信息,来不断提高路径跟踪的控制精度,主要研究了基于迭代学习控制算法的园区清扫车路径跟踪控制问题。采用智能PD型迭代学习控制算法,引入非线性不确定项作为补偿,消除清扫车转向控制中的实时变化的不确定扰动影响,具有很高的实际应用价值。仿真研究表明,迭代学习控制可以较好的利用清扫车循环运行的信息,提高路径跟踪的控制精度,且具有较强的抗扰能力,实现园区清扫车的高精度稳定跟踪控制。