基于橡胶减震器目标刚度曲线的多参数优化

王竹清,王 伟

(青岛科技大学 橡塑材料与工程教育部重点实验室,山东 青岛 266042)

一般,优化分为拓扑优化和参数优化,两种优化方式既可以同时应用于某一零件,也可单独用于产品设计。拓扑优化常用于刚度较大的金属零件及混凝土结构等,如胡海明等[1]对轮胎模具弓形座进行拓扑优化,李东斌等[2]基于应变能对桥梁结构进行拓扑优化。由于含有橡胶材料的数学模型有着复杂的非线性行为,很难通过解析求解的方法进行优化。因此,橡胶制品常需借助有限元方法进行参数优化,如黄祖宇[3]和孙蓓蓓等[4]以刚度曲线为目标函数分别对橡胶减震器和橡胶悬架进行参数优化。但同时对橡胶制品的尺寸和材料属性进行优化的相关文献较少,本研究通过在Isight平台上集成Abaqus和Data Matching模块,在仅知道橡胶本构模型参数范围和制品规定尺寸范围的情况下,同时对某车用橡胶减震器的本构模型参数和尺寸进行参数优化,使橡胶减震器的载荷－位移曲线符合目标刚度曲线。

1 橡胶减震器有限元建模

1.1 几何模型和有限元模型

本研究采用的橡胶减震器结构如图1所示。该橡胶减震器安装在汽车前桥和车架之间,在汽车行驶过程中,起到维持行驶高度和缓冲减震的作用。上下两部分为金属框架,用于连接汽车前桥和车架,嵌在金属架内的为橡胶结构,起到支撑和缓冲的作用。

图1 橡胶减震器的结构Fig.1 Structure of rubber damper

由于该橡胶减震器是上下对称的轴对称结构,因此仅需要提取其中一个四分之一截面,建立轴对称分析模型,网格模型如图2所示。橡胶属于不可压缩材料,故网格类型选用杂交单元CGAX4H。上下金属套简化为刚体。

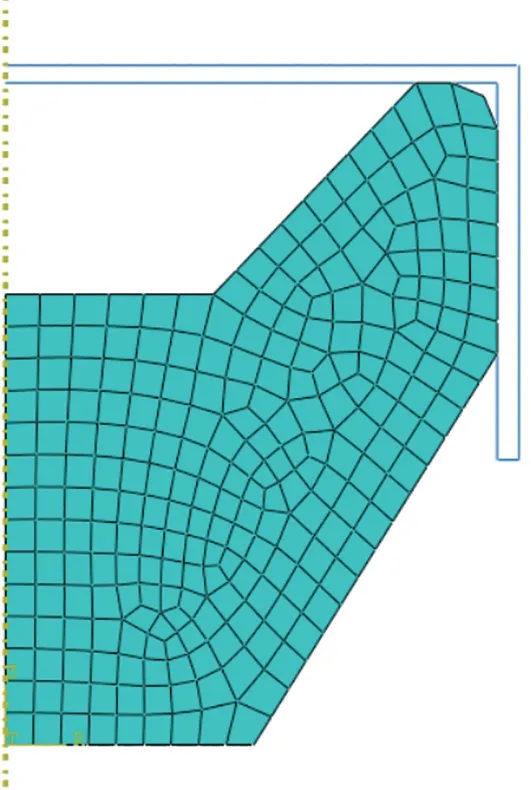
图2 橡胶减震器的有限元模型Fig.2 Finite element model of rubber damper

1.2 橡胶本构模型

橡胶是一种超弹性材料,具有应变大非线性强的特征。目前,用来描述橡胶材料最常用的本构模型是基于唯象理论的Yeoh模型和Ogden三阶模型。其中Yeoh模型是广义Mooney-Rivlin多项式的一种特殊形式,如式(1)所示:

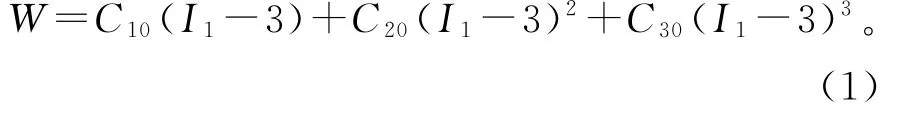
式(1)中:C10、C20、C30为材料常数,它们分别反映橡胶的模量、橡胶形变过程中的软化现象、橡胶的硬化现象,I1为第一Green应变不变量。

Ogden模型是采用主拉伸作为基准变量的本构模型,如式(2)所示:

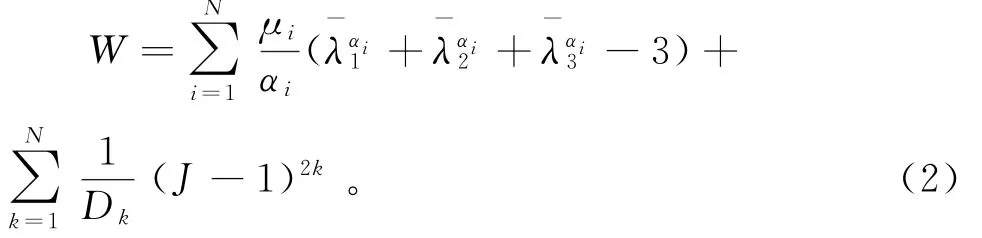
式(2)中:N为模型的阶数,J为弹性体积比,λ1、λ2、λ3为应变张量3个方向上的主伸长率,μi、αi为材料常数,Dk为反映橡胶不可压缩的参数。

要准确拟合上述两个本构模型,需要通过试验得到橡胶材料的拉伸、剪切和压缩状态下的力学性能。这些性能分别通过单轴拉伸试验、剪切试验和压缩试验获得,但在压缩试验中,橡胶试件表面摩擦力无法消除,侧面无法实现自由膨胀,误差较大,故常用等轴拉伸试验代替压缩试验。等轴拉伸试验通过一定数量等间距的夹子对橡胶试样进行多个方向等轴拉伸,可消除摩擦力带来的剪应变影响。由于能同时完成上述试验的国内单位很少,且测试价格昂贵。因此,若能根据橡胶制品的性能要求,反推出橡胶本构模型的参数,则具有非常重要的工程应用价值。由式(2)可知,Ogden三阶模型共有6个参数,会极大地增加反演计算难度,且Ogden模型在计算大应变时,易出现不收敛的情况[5]。由式(1)知,Yeoh模型仅含有3个参数C10、C20和C30,且其在大应变下收敛性好,计算效率高,故本研究采用Yeoh模型来描述橡胶减震器中的橡胶材料的非线性力学行为。

2 优化过程

2.1 优化三要素

优化在数学上被定义为:满足限定条件,求得最优解。求解优化问题有3大要素,分别为设计变量、目标函数和约束限制。在优化过程中允许改变的参数,被称为设计变量。目标函数是设计变量的函数,它是设计目的的具体体现。在优化过程中,设计变量的改变不是随意的,它必须符合数学逻辑以及一些工程规定。因此需要对设计变量施加约束条件,这些条件被称为约束限制。优化问题可以用式(3)简单描述如下:

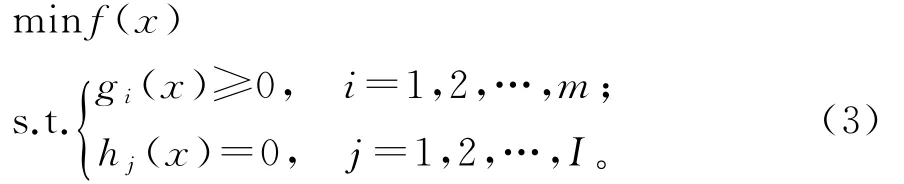
式(3)中,x为设计变量,f(x)为目标函数,gi(x)和hj(x)为约束限制。

在本研究中,橡胶本构参数和橡胶减震器关键尺寸为设计变量,评价橡胶减震器的刚度曲线与目标刚度曲线的差距为目标函数,橡胶本构参数和橡胶减震器关键尺寸的优化范围即为约束限制。

2.2 优化方法

在Isight中有3类优化方法,分别为梯度法、直接法和全局法。梯度法适用于线性函数求解,而含有橡胶材料的数学模型常具有非线性,故梯度法不适用于求解橡胶制品。全局法理论上能求得全局最优解,但随着参数数量增加,其计算时间成本大幅度增加,且易出现失败解[6]。直接法计算效率高,求解步长大,可用来求解非线性问题。因此,直接法在工程中得到广泛应用,但其缺点是计算结果一定程度上仰赖初值[7]。优化算法对初值的选择十分敏感,一个好的初值选取可在很大程度上降低优化计算量,增加计算精度。可通过DOE(design of experiments)试验方法,较方便地为直接法寻找一个合适的初值。

在Isight中直接法共有两种算法,分别为Downhill Simplex算法和Hooke-Jeeves算法,其中Downhill Simplex算法使用单纯形(simplex)的概念,通过改变单纯形的尺寸及顶点位置以探索设计空间,该方法求解跳跃性较大,而橡胶材料的参数优化不能进行很大的尺寸变动,这会产生较多失败解,影响计算精度。Hooke-Jeeves算法是通过一个罚函数值来探索设计空间,求解过程较为稳定,故本研究采用的直接法是Hooke-Jeeves算法[8],其最优解的求解步骤如下:

步骤1:给定初始点、初始步长和坐标向量分别为x(1)、t和e1,e2,…,en,令加速因子α≥1,缩减率0＜β＜1,使k＝i＝1,y(1)＝x(1);

步骤2:若f(y(i)＋tei)＜f(y(i)),正方向离散步探索成功,令

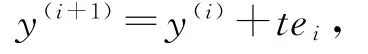
转步骤4;若f(y(i)＋tei)≥f(y(i)),正方向离散步探索失败,转步骤3;

步骤3:若f(y(i)－tei)＜f(y(i)),令

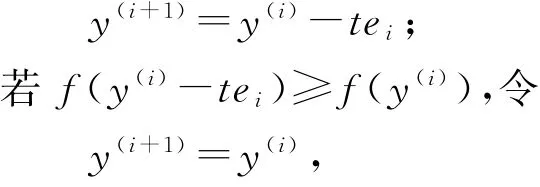
转步骤4;

步骤4:若i＜n,令i＝i＋1,返回步骤2;否则i＝n,若f(y(n＋1))≥f(x(k)),转 步 骤6;若f(y(n＋1))＜f(x(k)),则转步骤5;

步骤5:使x(k＋1)＝y(n＋1),令

使k＝k＋1,i＝1,返回步骤2;

步骤6:若t≤β,则迭代停止,得点xk;否则,令

使k＝k＋1,i＝1,返回步骤2。

2.3 本构模型的参数范围

在Yeoh模型中,C10反映橡胶的模量,C20反映橡胶形变过程中的软化现象,C30反映橡胶的硬化现象。根据常规橡胶的力学性能,给出这3个参数大致范围[9],如表1所示。

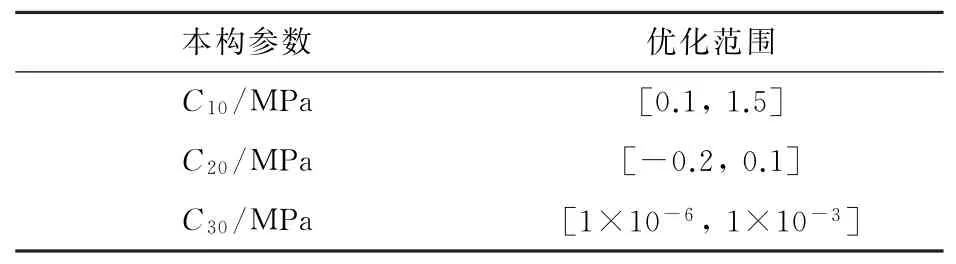
表1 本构模型参数的优化范围Table 1 Optimization range of constitutive model parameters

2.4 橡胶减震器的尺寸范围

对橡胶减震器的空腔高度H、空腔半径L以及橡胶体与下截面的外倾角R3个关键设计参数进行优化,各尺寸参数位置如图3所示。本研究参照文献[3]中给定的尺寸设计范围,如表2所示。

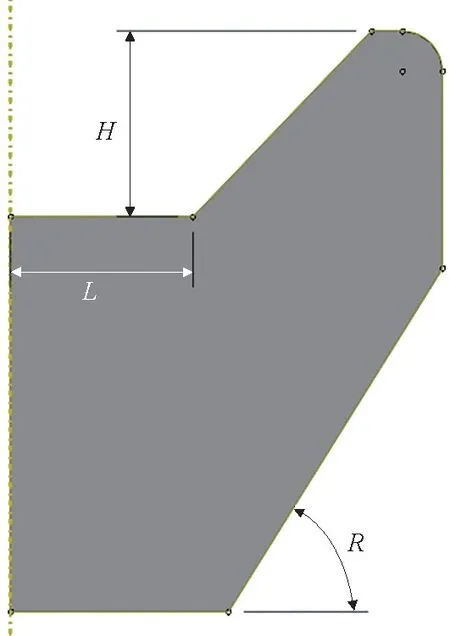
图3 橡胶减震器待优化尺寸Fig.3 Size of rubber damper to be optimized

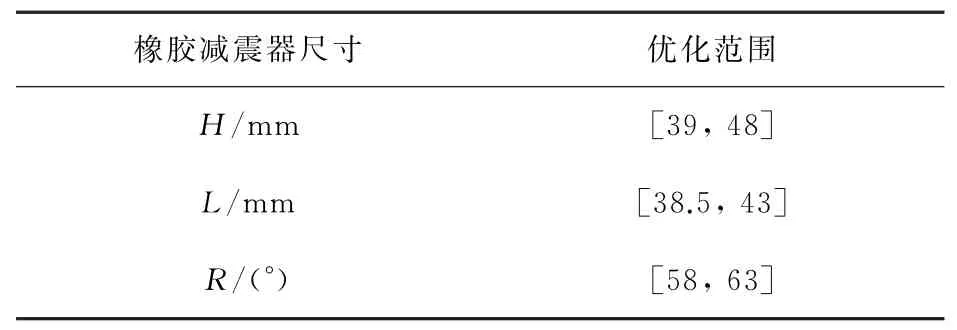
表2 橡胶减震器尺寸参数的优化范围Table 2 Optimization range of size parameters of rubber damper

2.5 正交试验预估初始值

由于设计变量有6个参数,它们包含橡胶减震器本构模型参数3个和尺寸参数3个。这会导致优化的计算量极其庞大,且不易找到全局最优解。因此,若能找到一个逼近全局解的初始值,会大大提高计算效率,增加求解准确度。通过DOE试验的方法可以快速地确定初始值,本研究采用正交数组方法(Orthogonal Arrays)安排这6个设计变量之间的试验组合[10],如表3所示。正交表格中共设计16组试验,其中C10、R、H和L参数采用4因子水平,C20和C30采用2因子水平。

表3 L 16(44×22)设计变量正交表Table 3 L 16(44×22)Orthogonal table of design variables

经过16组试验后,确定第6组试验组合求得的刚度曲线与目标刚度曲线最接近,故将第6组试验参数作为初值。此时橡胶减震器的初始刚度曲线与目标刚度曲线如图4所示。

图4 橡胶减震器初始刚度曲线与目标刚度曲线Fig.4 Initial stiffness curve and objective stiffness curve of rubber damper

3 目标函数及优化结果分析

在橡胶减震器的优化过程中,优化目标是缩小橡胶减震器的刚度曲线与目标刚度曲线之间的差距。本研究采用橡胶减震器刚度曲线与目标刚度曲线的面积差绝对值之和(sum of the absolute area difference)来衡量二者之间的差距,初始面积差绝对值之和为260.5。

利用Hooke-Jeeves算法进行优化迭代,共迭代101次,并在第95次迭代获得最优解,此时面积差绝对值之和为33.9。橡胶减震器刚度曲线与目标刚度曲线间的面积差绝对值之和在迭代过程中的变化如图5所示。

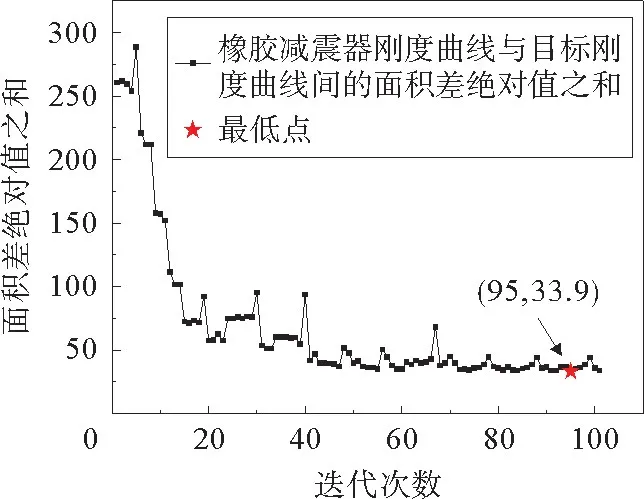
图5 橡胶减震器刚度曲线与目标刚度曲线间的面积差绝对值之和在迭代过程中的变化Fig.5 Variation of the absolute area differences between the rubber damper stiffness curve and the objective stiffness curve during iteration

在第95次迭代时,仿真刚度曲线与目标刚度曲线间的面积差绝对值之和的值最小,即为最优解,此时橡胶减震器的本构模型参数和尺寸参数见表4。利用经验公式E＝6C10和HA＝(100E－15.75)/(2.15＋E)可知[11],当C10为0.542 MPa时,杨氏模量E为3.252 MPa,邵A硬度HA为57.284(初步估计橡胶的邵A硬度在60左右),从而可以指导进行橡胶配方设计,给出满足橡胶减震器刚度性能要求的合理配方,这样会大幅度降低进行配方试验和力学性能测试的次数,缩短开发周期。

表4 橡胶减震器的最优本构模型参数和尺寸参数Table 4 Optimal constitutive model parameters and dimension parameters of rubber damper

当橡胶减震器的本构模型参数和尺寸参数均采用最优解时,橡胶减震器的仿真刚度曲线与目标刚度曲线如图6所示,此时两条曲线的相对误差为4.9%。

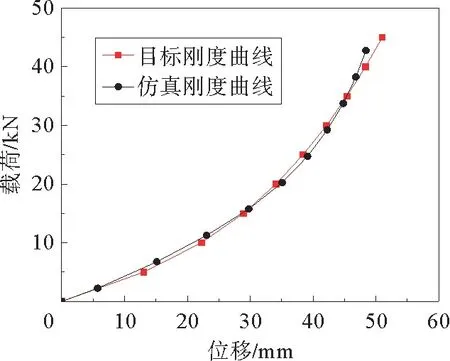
图6 优化后橡胶减震器刚度曲线与目标刚度曲线对比图Fig.6 Comparison of optimized rubber damper stiffness curve and objective stiffness curve

对比橡胶减震器优化后的刚度曲线与目标刚度曲线,可以看到二者尽管不能完全一致,但无论是在高压缩量还是低压缩量范围内,与目标刚度曲线的误差均较小。

4 结 论

1)通过Isight平台集成Abaqus和Data Matching模块,对橡胶减震器的本构模型参数和关键尺寸参数进行了多参数优化;

2)采用正交试验方法,确定多参数优化初值,大大提高了优化效率和准确度;

3)在正交试验的优化初值下,采用Hooke-Jeeves算法进行优化迭代,并得到了一组符合橡胶减震器目标刚度曲线的最优解。

通过对橡胶减震器的刚度曲线优化分析,本研究提出了一种可同时优化橡胶本构模型参数和橡胶制品结构参数,进而满足制品性能为目标函数的新方法,借助优化预测的本构模型参数可以反推橡胶的模量和硬度,为橡胶配方设计提供指导。