基于时间序列的结构应力监测信号预测方法
孙 晓,王清梅,楚敬敬
(1.青岛科技大学 自动化与电子工程学院,山东 青岛 266061;2.中国科学院国家天文台,北京 100012)
500 m口径球面射电望远镜FAST(five-hundredmeter aperture spherical telescope)为具有主动反射面的球冠状大型射电望远镜[1],建设于我国贵州,望远镜空间跨度大、结构复杂,为确保结构安全,使用传感器对其支撑钢结构关键点应力信息进行监测以评价其健康状态。其中,用于主索及圈梁钢结构应力监测的光纤Bragg光栅传感器共计416个[2]。应力信号可根据历史数据的变化趋势,对未来的结构应力进行预测,有助于提早发现结构可能存在的故障,进行预警或排查处理,提高结构安全性能。
目前国内外对于信号预测的主要方法有人工智能法、物理模型参数法、时间序分析列法等[3]。ZHANG等[4]利用有限元建模的方法,根据荷载来预测金属构件焊接面处的应力,用于识别薄板粘结构件的破坏。OZGUR等[5]使用机器学习中全卷积网络模型,结合材料本身特性对弹性材料中应力进行了预测,利用断裂力学可评估材料的强度。王培德等[6]提出利用多个当前荷载作为输入,基于位置神经网络模型预测风电机组应力极值的方法,来提高风电机组的应力预测精度。王苏健等[7]使用历史数据与随机森林的方法对矿井围岩应力进行了预测,将其用于监测数据缺失插值,取得了较好的插值效果。薛磊等[8]基于BP神经网络和改进后的PSO-BP神经网络、GABP神经网络研究了风电塔筒应力预测,通过测试选取了最优的预测模型。相关研究均取得了较好的预测效果,但部分方法需要详细的结构特性信息,或相关荷载信号作为参考输入。其中人工智能法容易陷入局部最优,影响预测精度;物理模型参数法参数评估较为困难且建模过程复杂;时间序列法应用中运算速度较快,但在长期预测中精度易受影响。
时间序列分析法[9]是从自相关的角度揭示信号序列的发展规律,认为任何一个时间序列都可以分解为确定性序列和随机项序列的叠加,拟合恰当的数学模型来描述序列值之间的统计规律,挖掘时间序列数据的趋势、周期性、循环规律等,进而利用这个模型来预测序列未来的趋势。ARIMA模型(autoregressive integrated moving average model)即差分自回归移动平均模型[10],用于描述依赖于时间的随机变量之间的延续性和相关性[11],是单变量的时间序列预测分析方法之一。与传统方法相比,不仅考虑了数据时间上的依存性,也考虑了随机波动的干扰,具有模型构建简单,只依赖数据本身内生变量即可实现预测等优点。
FAST大型射电望远镜在工作过程中,若望远镜工作状态发生改变,如进行主动反射面变形,结构拓扑将发生改变,同一测点的结构受力规律将有较大变化。其结构应力监测信号的预测,主要关注短期内的信号估值,即数分钟后的结构信息,以此进行状态估计与预警,而非长期预测。本研究选择时间序列分析法,基于ARIMA模型,研究FAST结构应力监测信号的预测方法,使用二阶差分将信号平稳化,结合信号自相关与偏自相关图以及赤池信息准则对模型完成定阶,并应用实测数据评价了模型预测效果。
1 数据预处理
光纤Bragg光栅应变计输出原始信息为调制的波长信号,与被测点应变值存在对应关系,当温度、应变变化范围不大时,传感器输出波长信号为
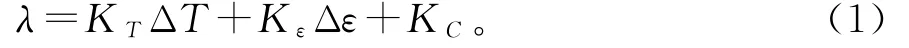
其中:ΔT为温度荷载变化值,Δε为监测应力变化值,KT为温度灵敏系数,Kε为应变灵敏系数,KC为常数。实际应用中,温度项对应变的干扰可通过温度补偿剔除,为简化分析,本研究直接使用传感器输出原始波长信号进行预测。
提取2019年7月17日1号测点原始输出波长信息,由于监测信息采样周期较短为1 s,经数据采集系统剔除无效异常值后,数据库中每日数据累计近7万条,为降低数据量,先对数据进行采样压缩处理。作为结构应力测点,其主要有效负荷变化周期较长,选择采样压缩周期Ts为120 s,满足采样定理fs>2fmax要求。设原始数据样本索引为i,原始数据序列为λorigin,序列长度为Norigin,保留每个数据点对应的实际采样时刻,采样后数据序列λs为

原始测量信号中,常包含测量误差、系统误差、噪声干扰和局部跳变等问题,致使数据存在不平滑异常。对压缩数据使用移动平均(moving average,MA)[12]消除压缩数据中此类异常的影响,使数据曲线更为平滑。移动平均可过滤系统中存在的高频和周期性误差,常用计算方法有,简单移动平均和加权移动平均等类型,使用简单移动平均法,计算公式为
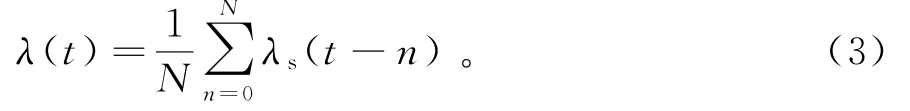
其中:λ(t)为变量λs(t)移动平均后的值,N是移动平均窗口的大小。选择N=10,对压缩数据序列λs进行移动平均后,得到移动平均信号数据序列λ作为本研究实际监测值,压缩数据与移动平均数据如图1所示。
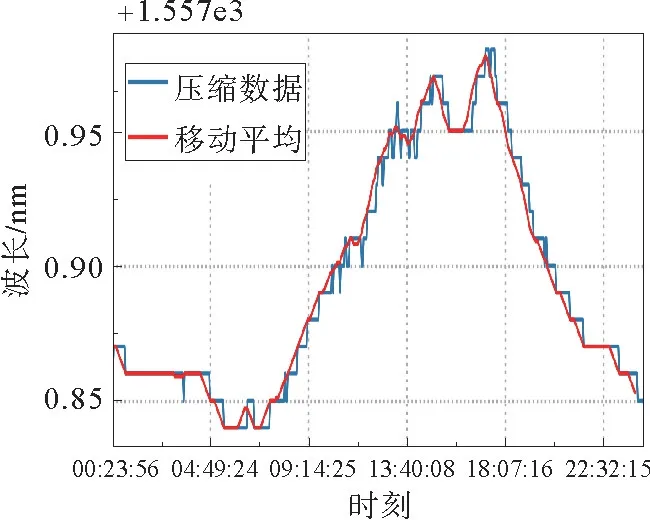
图1 压缩数据与移动平均数据Fig.1 Compressed data and moving average data
2 ARIMA预测模型算法
ARIMA模型是在自回归模型(AR)和滑动平均模型(MA)基础上发展出的方法,通过差分法将非平稳时间序列平稳化,克服AR模型和MA模型仅可处理平稳时间序列的缺点,广泛应用于经济增长、人口数量变化、市场价格变化、工程监测信号预测等领域[13-14]。ARIMA模型记为ARIMA(p,d,q)算法模型一般表达式为
其中:B为差分延迟算子,Φ(B)为自回归系数多项式,Θ(B)为移动平均系数多项式,Xt为原始信号,εt是均值为0的白噪声序列,p为AR模型阶数,q为MA模型阶数,d为差分阶数,当q为0时模型退化为AR模型,d为0时退化为ARMA模型,p为0时模型退化为MA模型,其更一般的表达形式为
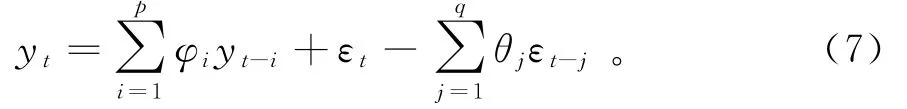
其中:yt为算法在t时刻的输入信号的预测值,可输入差分信号,φi,θj均为待估参数。在实际应用中,主要包括检验时间序列平稳性与处理,模型定阶,模型检验及预测4个步骤。
2.1 平稳性检验与处理
观察作为实际值的原始信号数据序列λ可见其存在明显的趋势并不平稳,对其做一阶与二阶差分,组成两个新的序列,d次差分方程:

其中:B为延迟算子,ωt为差分后的数列。
利用单位根检验法(ADF检验)对其进行平稳性检验,若存在单位根,说明序列不平稳。检验结果如表1所示,分析可知,一阶与二阶差分信号检验结果为-3.979 292与-6.636 427,均小于各水平临界值,检验统计量接近于0,拒绝原假设,不存在单位根,属于平稳信号,其中二阶差分平稳性更好,本例选二阶差分作为输入信号,定阶d为2。
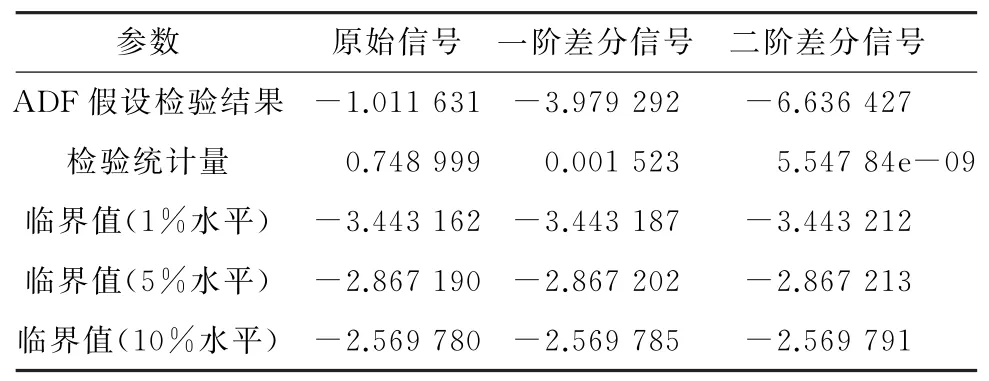
表1 ADF单位根检验Table 1 ADF Test
2.2 模型定阶与训练
通过绘制自相关ACF与偏自相关PACF图像,分析偏自相关函数图的拖尾性、截尾性,通过曲线第一次穿过上置信区间的横坐标确定p、q值,自相关ρk与偏自相关φkk函数表达式[15]为
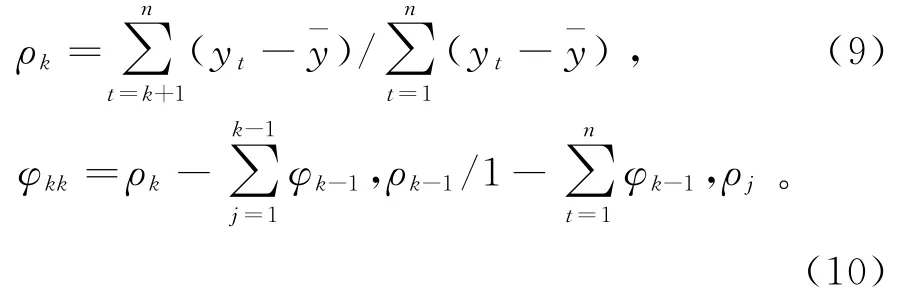
其中:yt表示t时刻随机序列取值,¯y表示其均值,φkk=φk-1,φkkφk-j,二阶差分信号自相关图(ACF)与偏自相关图(PACF)如图2所示。
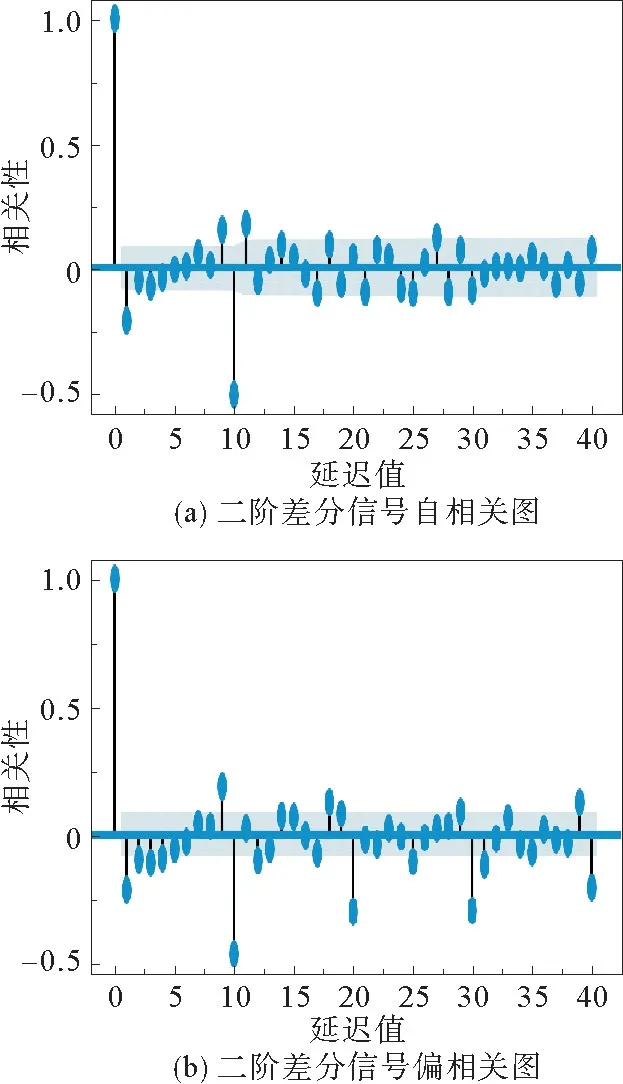
图2 二阶差分信号自相关与偏自相关图Fig.2 ACF and PACF of second order differential signal
可见ACF图在9、10、11阶有异常凸起,PACF在9、10、20、30、40处也有明显凸起,并非完全截尾。进一步确定参数可结合最小AIC准则即赤池信息准则[16]确定,选择AIC值最小的模型,AIC一般计算公式为

其中:K为参数数量,L为似然函数。
最终选择p,q为4,9,建立ARIMA(4,2,9)模型,其AIC值为-6 453.6。使用信号二阶差分序列进行训练得模型系数为
常数项:0.224 871 8;
AR系数:-28.824 789 52,-17.974 262 53,-16.771 701 12,-21.589 047 91;
MA系数:0,0,0,0,0,1.836 826 01,0,3.078 208 63,3.798 704 94。
3 预测与结果评价
为评价模型预测结果,使用均方根误差RMSE进行评价,考虑了真实值与误差值的差值与样本容量的比值,公式为
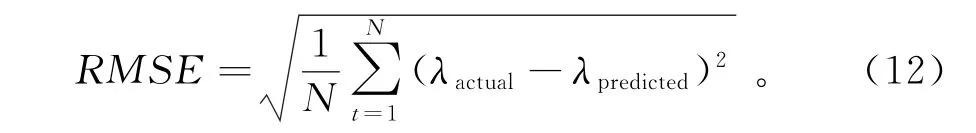
其中:λactual为真实值序列即λ,λpredicted为模型预测差分值还原后对应的预测信号序列。差分信号实际值与预测值如图3所示。
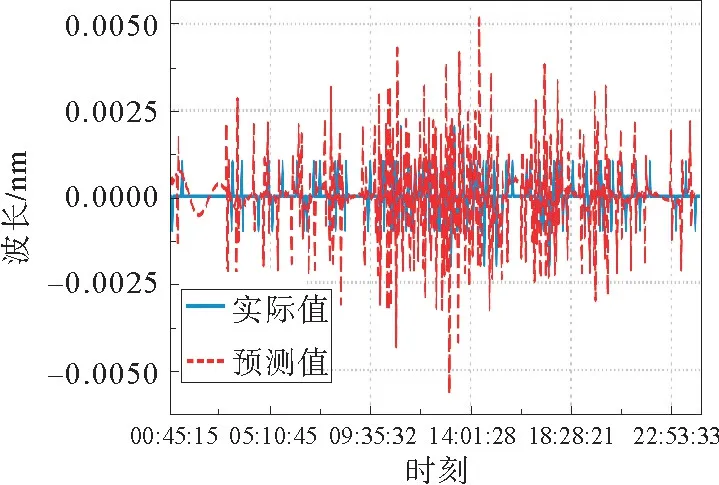
图3 二阶差分信号实际值与预测值Fig.3 Actual value and predicted value of second order differential signal
可见差分信号的实际值与预测值规律一致,但是幅值有较大差别,实际上,差值与原始信号比值非常小,还原为原始序列后,如图4所示,图中为方便区别,预测值向左平移绘制。还原后模型拟合曲线与真实值几乎完全重合,RMSE=0.001 3 nm,可见模型预测效果良好。
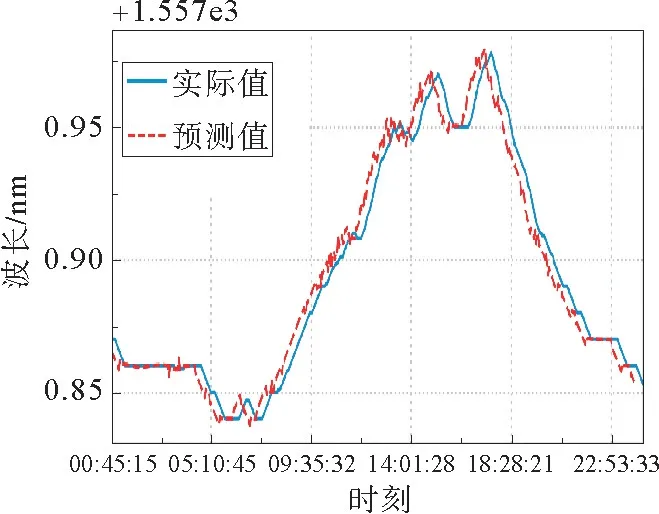
图4 实际值与模型拟合预测值Fig.4 Actual value and model predicted value
应用该模型进行短期预测,每次预测为使用历史数据对下一采样周期值的预测,对应实际信号,预测的提前时间为120 s,可见短期内信号预测效果良好。也可使用模型预测值本身,对未来较长一个时间段内进行预测,应用ARIMA(4,2,9)模型,将实际值数据序列λ进行分割,前70%数据作为训练集进行训练,使用模型对剩下30%的测试集部分进行预测并比较,重复前述步骤,结果如图5所示。

图5 长期预测实际值与预测值Fig.5 Actual value and model predicted value in long-term
预测结果在一定程度上可反映信号变化趋势,但是预测值与真实值之间存在较大偏差,RMSE=0.179 1 nm。主要由于数据采样点较密集,30%测试序列包含了160个数据点,监测值变化与数值本身数据量比值较小,接近千分之一,差分信号内在趋势规律不够明显。长期预测中,预测结果与对模型阶数非常敏感,容易出现过拟合状态,需合理定阶。
4 结 语
使用ARIMA模型对FAST结构应力监测信号进行预测,需对信号进行差分平稳化,预测结果还原后,在长期预测中,ARIMA模型可以反应信号变化趋势,但存在较大误差。但短期内预测结果RMSE=0.001 3 nm,模型预测精度高。本研究中预测提前时间为2 min,若想延长预测时间,在数据压缩阶段可增加采样周期,如改为600 s,即可实现提前10 min的预测,测试依然具有较高的预测精度,满足FAST结构应力监测信号的应用需求。
方法利用结构应力信号时序上的依存性,采用ARIMA模型,仅依赖监测数据本身内生变量实现结构应力的预测,不需要复杂的结构物理模型建模或其他相关荷载信息的支持,既考虑了应力的发展趋势规律,也考虑了随机波动信号的干扰,其预测结果有利于结构异常状态的早期预警。

