考虑粗糙度下的三叉杆万向联轴器的热弹流润滑特性分析

魏建宝,李松梅

(青岛科技大学 机电工程学院,山东 青岛 266061)

本课题组发明的三叉杆滑块式万向联轴器是一种具有自主知识产权的新型等角速万向联轴器,该联轴器具有结构紧凑、传输能力强、安装方便等显著特点[1-3]。三叉杆联轴器的滚珠轴承与滑块之间的点摩擦会降低联轴器的传输能力,影响联轴器的工作效率,而润滑是降低摩擦阻力的一项重要技术举措。弹性流体动力润滑理论是研究在相互滚动或伴有滑动的滚动条件下,两弹性物体接触间的流体动力润滑膜的力学性质,热弹流理论中进一步考虑了剪切热的影响,通过建立接触面间的弹性方程、黏压方程和流体润滑的主要方程,来获得接触区域的油膜压力分布、润滑膜厚度分布、温度分布及摩擦系数。

文献[4]采用顺解法对椭圆接触进行了数值求解并对点接触膜厚计算公式进行了拟合。LUBRECH[5]首次提出采用多重网格法来求解点接触的EHL问题,通过改变网格密度来提高求解精度并降低计算量。EVANS等[6]发表了点接触问题逆解法的研究报告。LIU等[7-8]分别基于Newtonian流体模型运用有限长线接触热弹流理论对倾斜滚子副进行了研究。王优强等[9]在LARSSON的基础上考虑了热效应的影响,在不考虑轮齿表面粗糙度的情况下求解了渐开线直齿轮非牛顿瞬态热弹流润滑的完全数值解。徐雨田等[10-11]针对三叉式联轴器在没有考虑粗糙度的情况之下进行了点接触等温及热弹流润滑分析,得到了接触区的油膜膜厚、压力、温度的变化曲线。由以上分析可以看出对于点接触式摩擦润滑分析做了很多相关研究,由于三叉杆滑块式联轴器在实际应用当中,滚珠与滑块的接触,在现有的技术当中难以做到将表面加工成理想光面,所以在考虑粗糙度的情况下进行润滑性能分析是非常有必要的。因此本工作以弹流润滑点接触理论为基础,在考虑粗糙度的情况下,对三叉杆滑块式万向联轴器进行了热弹流润滑性能分析研究。

1 点接触模型

新型三叉式万向联轴器的滑块与三叉槽接触面间通过滚珠结构将滑动摩擦改变为滚动摩擦,滑道内润滑油充足,工作过程中滑块滑动带动滚珠滚动,接触面间可看作点接触[12],简化模型如图1所示。图1中,滚珠为球体,滑块表面指向三叉槽轴线方向为x方向,滑块表面垂直于三叉槽轴线方向为y方向,垂直于滑块表面且指向滚珠球心为z方向,滑块沿三叉槽轴线往复运动,亦即沿x方向进行移动。

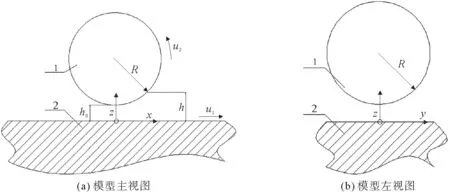
图1 三叉式万向联轴器滑块滚珠润滑简化模型Fig.1 A simplified model of ball lubrication for the sliding block of the trigeminal universal joint

2 控制方程

2.1 Reynolds方程

主要以点接触类型进行润滑分析,给出二维Reynolds方程[13],如式(1)所示:

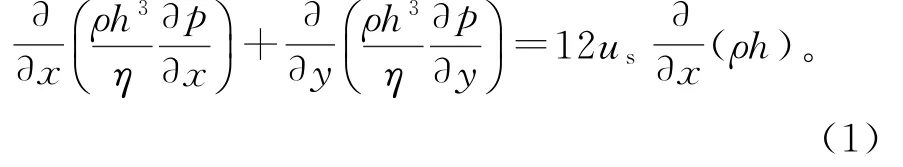
其中,2us＝u1＋u2。us为相 对速度,u1、u2为 滑块,滚珠速度。ρ为润滑油密度,η为润滑油黏度,h为膜厚。

膜厚方程[14]如式(2)所示:

其中,R为滚珠半径,v(x,y)表示的是弹性变形,如式(3)所示,r(x,y)表示的是粗糙度变形,正弦粗糙度r(x,y)＝DAsin(2πx)。

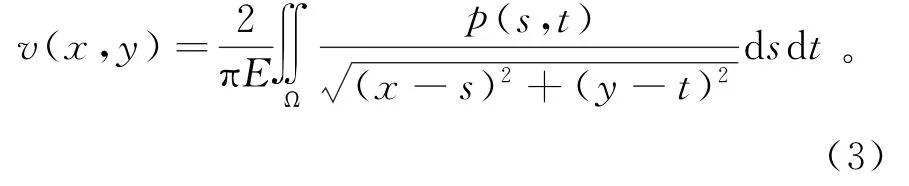
能量方程如式(4)所示:

式(4)中:cp为润滑油比热容,T为温度,u为x方向上速度分量,ww为z方向上速度分量。

黏压温方程如式(5)所示:

其中:η为润滑油黏度,η0初始润滑黏度,ρ0为初始润滑油密度。

密压温方程如式(6)所示:

其中:D为密温系数;T0为初始温度。

2.2 量纲一化方程

能量方程量纲一化,式(7)所示:

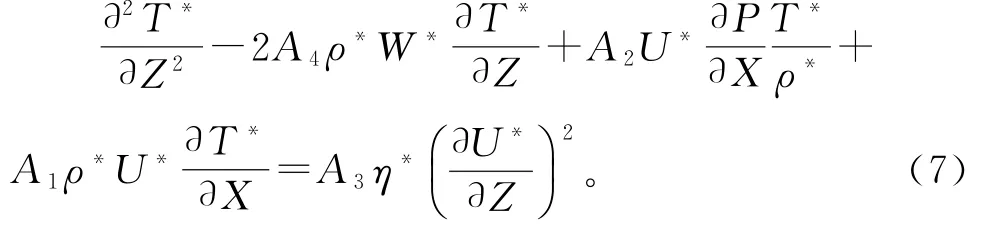
压力量纲一化方程:

膜厚量纲一化方程:

黏压温量纲一化,如式(10):

密压温量纲一化,如式(11):

2.3 差分方程

Reynolds方程离散形式,如式(12)所示:

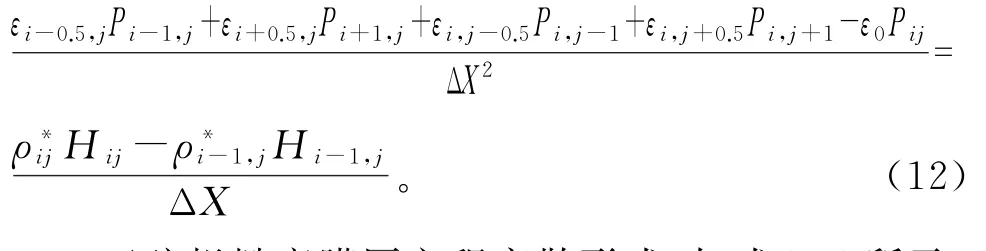
正弦粗糙度膜厚方程离散形式,如式(13)所示:

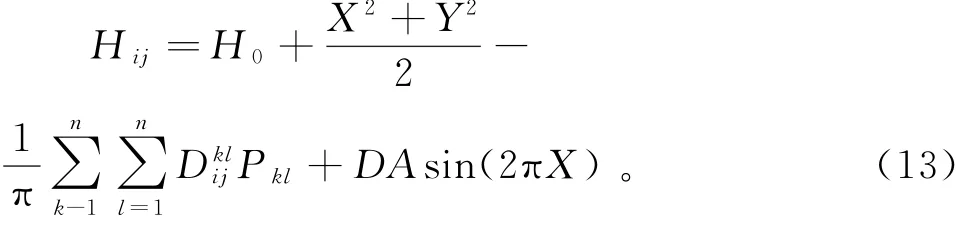
载荷方程离散形式,如式(14)所示:

3 边界与初始条件

节点数N＝65×65,量纲一化处理X方向起终点坐标为X0＝－2.5和XE＝1.5;量纲一化处理Y方向起终点坐标为Y0＝－2.0和YE＝2.0;R取0.002 m,Us为1.0 m·s－1。在进行润滑特性求解时采用多重网格法进行计算,每一瞬时压力计算的迭代初值使用前一瞬时压力迭代的结果,迭代收敛判据为每个瞬时压力和载荷的相对误差小于0.001。润滑油应用P100型号,具体参数为:η0＝0.214 Pa·s,α＝2×10－8Pa－1,ρ0＝870 kg·m－3。

考虑粗糙度时,用正弦粗糙度进行考察[15-16],考虑粗糙度的幅值取值时,本研究所述三叉式万向联轴器属于传动零件,在实际的应用当中,滚珠与滑块会产生相对滑动,本研究对3个批次的三叉杆万向联轴器的滑块表面粗糙度进行了测量。得到了3个批次表面粗糙度的平均值分别为0.025,0.023,0.028μm。为了使分析更符合实际测量情况以及方便考察粗糙度值对联轴器润滑程度的影响,分别使粗糙度幅值(DA)取0.01、0.02和0.03μm,频率设置为1 Hz,粗糙度的图像如图2所示。

图2 正弦粗糙度幅值变化幅值Fig.2 Sinusoidal roughness variation amplitude graph

4 结果与讨论

通过膜厚三维图难以看出粗糙度对膜厚的影响,给出的最大粗糙度幅值为0.03 mm的膜厚分布与幅值为0的膜厚分布趋势几乎相同;由图3(b)～(e),在X方向上,接触区的膜厚值围绕理想膜厚值产生波动。随着粗糙度幅值升高,接触区膜厚变厚,在接近中心区域的位置产生了凸起峰值,这是由于此处的压力值增大处于峰值;Y方向膜厚呈对称分布,且膜厚的变化量很小。由图3(d)可知,膜厚在接触区始端边缘随粗糙度幅值增大而变厚,接触中心点附近膜厚随粗糙度幅值升高而变厚,整个凸起的部分略有变窄。热效应下对膜厚的影响不是很大,主要是在于温度升高不利于膜厚的形成。

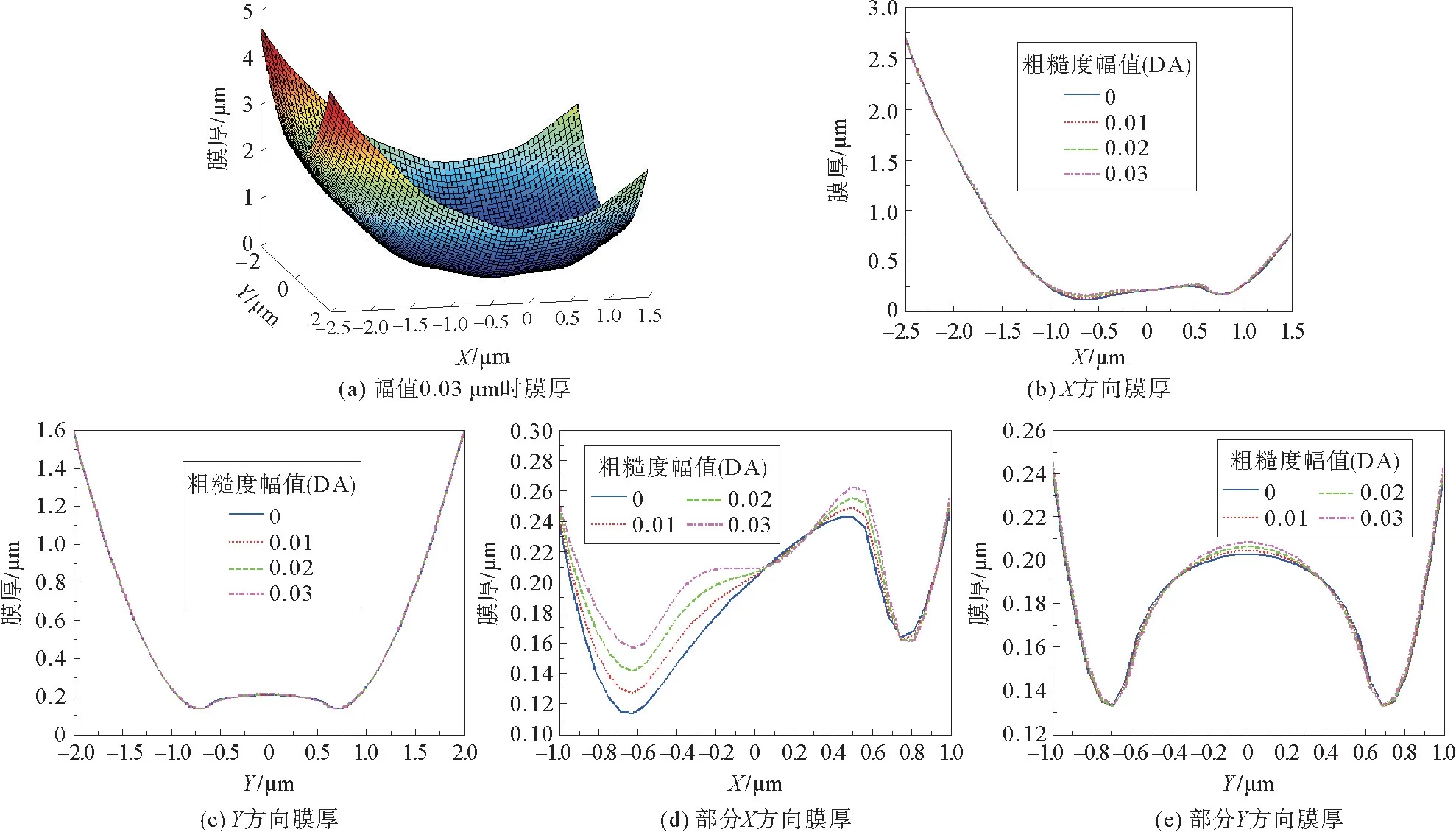
图3 正弦粗糙度幅值下的膜厚分布曲线Fig.3 Graphs of film thickness distribution curve under sine roughness amplitude

由图4(a)～(c)发现,随着正弦粗糙度幅值的升高,接触区的压力峰和二次压力峰间的沟壑深度加大;由图4(b)可知,在X方向上,随着粗糙度幅值的升高,第一压力峰的位置明显向入口区移动,且压力值明显增大,二次压力峰位置往出口区移动明显,而且压力值呈增大趋势,靠近接触中心至二次压力峰之前的部分压力有所降低;由图4(c)可知,Y方向的压力呈对称分布且略有降低。说明在考虑粗糙度的热效应下对点接触区压力产生的影响较明显。

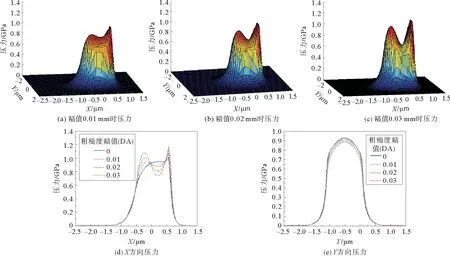
图4 正弦粗糙度幅值下的压力分布曲线Fig.4 Graphs of pressure distribution curve under sine roughness amplitude

由图5(a)～(c)可知,温度分布趋势与压力分布趋势相似,随着粗糙度幅值的增大,接触区域的温度峰和二次温度峰之间的沟壑深度加大;由图5(b)可知,在X方向上,温度值随着粗糙度幅值的增大而升高,温度值明显增加,在接近中心区域处形成第一温度峰,并且温度峰位置随着粗糙度的增加明显向入口区移动。二次温度峰位置向出口区移动明显,接触中心至二次温度峰之间的部分温度有所下降,由图5(c)可知,Y方向的温度以接触中心对称且上升。说明在考虑粗糙度的热效应下对点接触区温度产生的影响较明显。

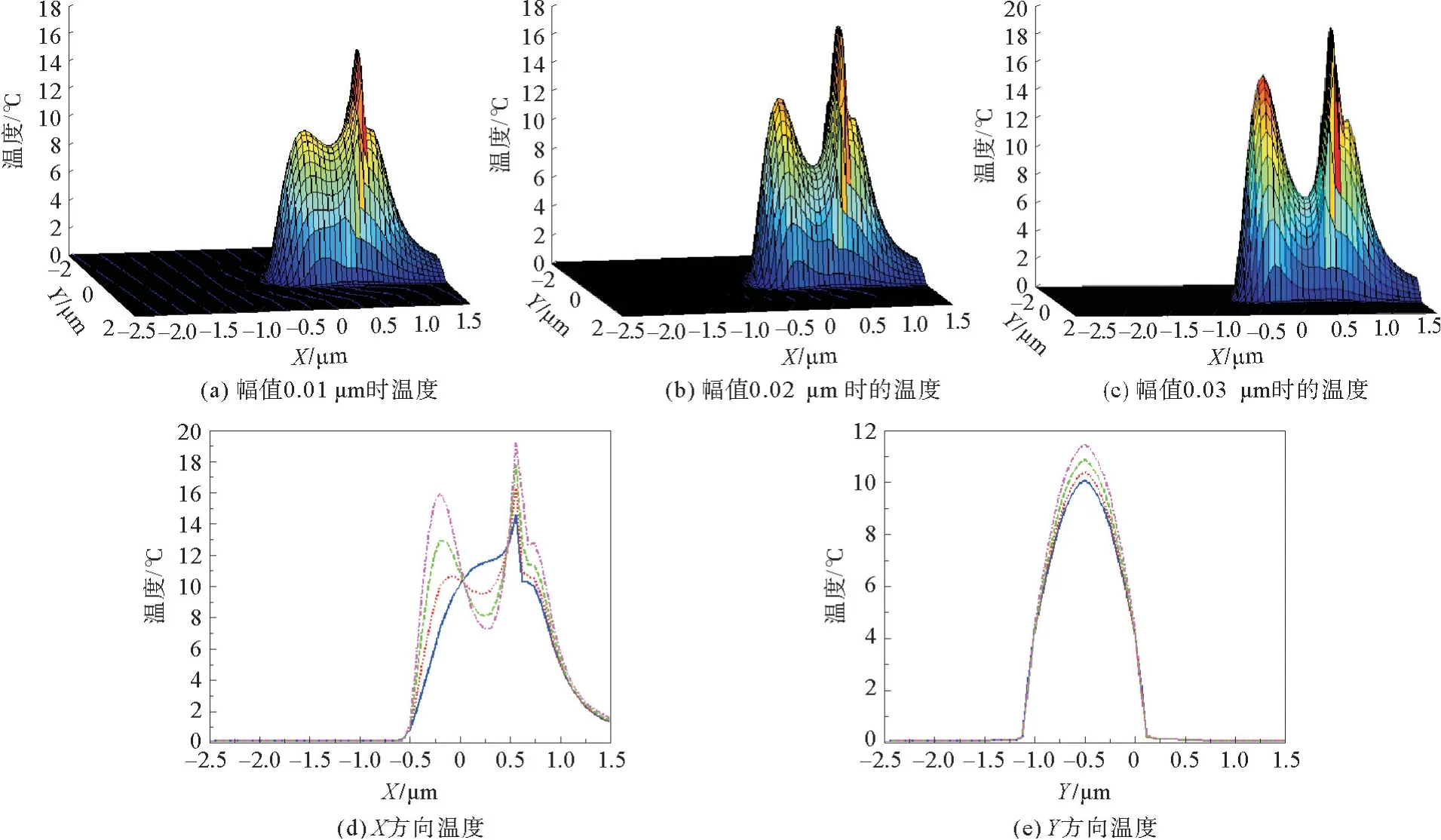
图5 正弦粗糙度幅值下的温度变化曲线Fig.5 Graphs of temperature change curve under sine roughness amplitude

由以上分析可知,与以往未考虑表面粗糙度的热弹流润滑分析相比,由于计入了粗糙度的影响因素,接触区的膜厚、压力、温度均发生了明显变化,尤其是压力与温度出现了明显的波动现象,且随着表面粗糙度的增大,波动的程度也在增大。而且在接触区域的中间以及末端位置,膜厚的变化量最大,压力与温度出现峰值,在实际的应用当中粗糙度是非常值得注意的因素。

4.1 速度因素影响分析

粗糙度设置频率为1 Hz正弦波,幅值为0.02 μm,在进行考察滚珠与滑块相对速度对润滑特性影响时,为了符合实际应用,按照汽车传动轴的日常应用合适的转速在1 500～3 000 r·min－1,以及通过对三叉式万向联轴器的滚珠速度的实际测量,可求得滚珠与滑块的相对速度范围为0.25～0.4 m·s－1。在分析时,为了贴合实际情况采用控制变量法分别取相对速度为0.2,0.3和0.4 m·s－1来考察速度对润滑特性的影响。膜厚、压力和温度的变化趋势如图6～图8所示。

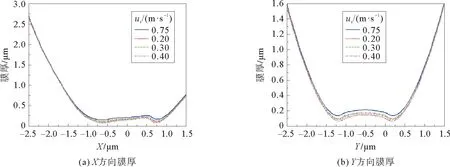
图6 正弦粗糙度幅值下的膜厚随速度变化的曲线Fig.6 Graphs of film thickness change with speed under sinusoidal roughness

图8 正弦粗糙度幅值下的温度随速度变化曲线Fig.8 Graphs of temperature distribution with speed under sinusoidal roughness

由图6可以看出,在粗糙度幅值为0.02μm的情况下,随着相对速度的增加,X方向的接触区膜厚明显越来越厚;Y方向膜厚对称分布,且随相对速度的加快而变厚,形状几乎不变。由图7可以看出,随着相对速度的提升,X方向接触中心区以前的压力明显增强,整体位置向出口区移动;Y方向压力对称分布,且随相对速度的提升而增大。由图8可以看出,随着相对速度的提升,X方向接触区温度值明显上升,温度峰出现的位置向入口区移动,二次温度峰向出口区移动;Y方向压力对称分布,且随相对速度的提升而升高,形状越陡峭。因此在实际的应用当中,高速情况下考虑热效应是非常有必要的。

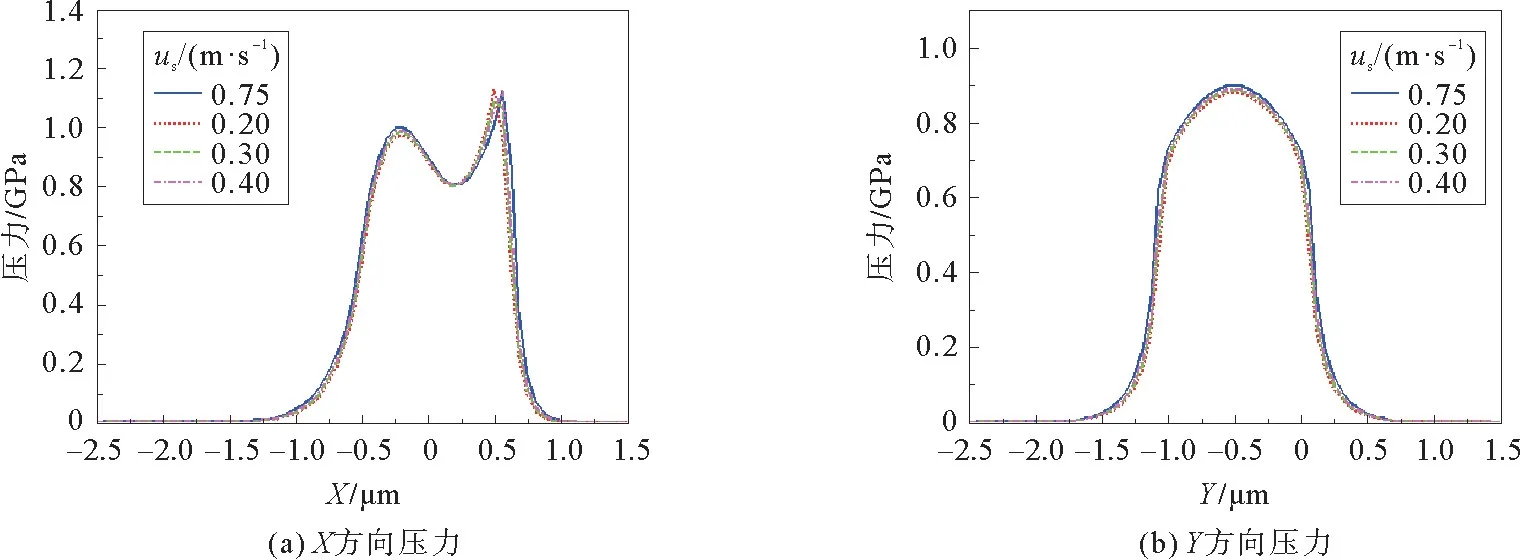
图7 正弦粗糙度幅值下的压力随速度变化曲线Fig.7 Graphs of pressure distribution with speed under sinusoidal roughness

4.2 滑滚比因素影响分析

滑滚比受到三叉杆万向联轴器滚珠与滑块速度的影响,但是由于加工工艺和制造条件的不同,即使是在相同的滚珠与滑块速度下,滑滚比也会有所不同。对不同批次的三叉式万向联轴器进行滑滚比测量时发现滑滚比的测量值范围为0.3～0.6之间,为了使分析更符合实际情况,采用控制变量法改变滑滚比分别取0.3,0.4,0.5和0.6,考察改变滑滚比对润滑特性的影响趋势。膜厚、压力和温度分布如图9～图11所示。

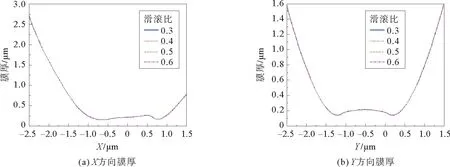
图9 正弦粗糙度幅值下的膜厚随滑滚比变化曲线Fig.9 Graphs of film thickness change with slip-roll ratio under sinusoidal roughness

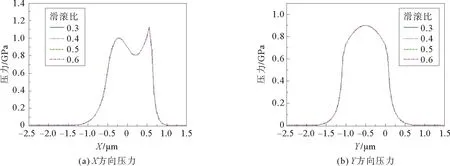
图10 正弦粗糙度幅值下的压力随滑滚比变化曲线Fig.10 Graphs of film pressure distribution with slip-roll ratio under sinusoidal roughness

图11 正弦粗糙度幅值下的温度随滑滚比变化曲线Fig.11 Graphs of temperature distribution with slip-roll ratio under sinusoidal roughness

由图9～10可以看出,随着滑滚比的增加,膜 厚、压力在X方向和Y方向没有出现明显变化,由图11可以看出,随着滑滚比的增加,接触区域的温度明显升高;在X方向上,随着滑滚比的增大,温度值不断升高,第一温度峰向入口区移动,第二温度峰向出口区移动;在Y方向上呈现对称分布,且温度随滑滚比的增大而升高。

5 结 论

1)以正弦粗糙度为分析条件进行了粗糙度考察,通过对点接触润滑方程进行量纲一化处理,然后对处理后的方程进行差分处理,利用多重网格法进行了求解,得到了润滑特性满意的收敛解。

2)随着表面粗糙度的增大,压力和温度也随之增大。从滑块长度方向看,在接触区域的中间及出口区位置,膜厚的变化量最大,压力与温度出现峰值。油膜膜厚、温度受滚珠与滑块的相对速度影响较大,随着速度的增加,膜厚、温度随之增加。滚滑比对温度影响较大,对膜厚、压力影响较小,滚滑比越大,温度越高。

3)在汽车传动轴上应用三叉杆滑块式万向联轴器时应当注重滑块的表面质量,严格控制其表面粗糙度值,选用合适的滚珠与滑块之间的滑滚比值,以达到最优的的润滑性能。