双螺母滚珠丝杠副导程误差与摩擦力矩关系研究
祖 莉 林炜国 张鲁超,2 欧 屹 王 凯,2
(1.南京理工大学机械工程学院, 南京 210094;2.数控机床功能部件共性技术工业和信息化部重点实验室, 张家港 215600)
0 引言
双螺母滚珠丝杠副通过改变垫片厚度控制滚珠丝杠副预紧力,具有传动效率高、定位精度好、反向间隙小等优点[1-2],被广泛应用于数控机床和农业机械传动与执行系统。但滚珠丝杠存在导程误差,这直接影响滚珠丝杠副的定位精度和使用性能。摩擦力矩是滚珠丝杠副的重要性能指标之一[3],直接决定滚珠丝杠副的使用情况。因此,不可忽视导程误差对滚珠丝杠副摩擦力矩的影响。
滚珠丝杠副摩擦力矩的计算多从预紧力计算入手。胡建忠等[4]通过坐标变换计算了双螺母滚珠丝杠副的轴向预紧力;崔高尚等[5]分析了双螺母滚珠丝杠副预紧力与垫片预紧量的关系;ZHOU等[6]基于经验公式提出新的摩擦力矩计算模型;王恒等[7]分析了反向器对摩擦力矩的影响。上述研究将滚珠视为受力相同,且未考虑导程误差的影响,而实际情况并非如此。
为准确描述各滚珠受力情况需对滚珠丝杠副进行载荷分析。MEI等[8]分析了丝杠、螺母变形以及几何误差对载荷分布的影响;刘畅等[9]分析了加载前后滚珠接触角的变化;CHEN等[10]通过载荷计算发现,相位角不同的滚珠,其载荷分布情况也不同;ZHEN等[11]基于载荷分布计算了滚珠丝杠副的疲劳寿命;基于文献[11]理论,LIN等[12]、ZHAO等[13]研究了考虑倾覆扭矩和滚道形状误差的滚珠载荷分布;BERTOLASO等[14]通过试验测量了滚珠接触角与接触载荷,但将各滚珠视为均匀受力,导致测量存在偏差;DU等[15]通过测量接触刚度间接反映滚珠变形量。上述对载荷分布的研究着重于滚珠变形和受力,忽略了尺寸误差尤其是丝杠导程误差对载荷分布和接触角的影响,同时,对载荷分布结果缺乏试验验证。
本文基于载荷和变形协调理论,分析导程误差对载荷分布的影响,通过分析提出双螺母滚珠丝杠副导程误差与摩擦力矩的关系模型,对不同精度等级丝杠的导程误差进行测量,并将各丝杠分别与同一套螺母、垫片、滚珠装配组成丝杠副,测量其摩擦力矩,并进行试验验证。
1 导程误差对载荷分布的影响
1.1 载荷分布模型
图1为垫片式双螺母滚珠丝杠副,垫片使左右螺母轴向移动进而挤压滚珠发生形变,产生预紧力,调整垫片厚度可改变预紧力。导程误差为滚珠丝杠单个导程的实际长度与理论长度的差值,图2为滚珠丝杠导程误差曲线,反映包含多个导程的一段行程内的导程误差之和,由于各导程误差有一定的波动性,通过直线拟合得到平均导程误差ET,ET的斜率即为滚珠丝杠导程误差ΔPh。为克服工作过程中由温度升高或负载引起的轴向伸长[16],导程误差一般小于0。
图3为双螺母滚珠丝杠副受力分析图,只承受预紧力时,左右螺母受力大小相等方向相反,均为FP,进行载荷分析时,可将左右螺母看作2个单螺母滚珠丝杠副进行受力分析,本文以右螺母为研究对象。以滚珠丝杠副常见的受力方式(丝杠轴受拉,螺母固定在基座上受压)为例,如图4所示,设加在滚珠丝杠轴上的轴向力为Fa,将第i-1个滚珠和第i个滚珠与丝杠、螺母接触点之间的丝杠、螺母部分分别称为丝杠和螺母的第i个单元,Fsi和Fni分别为丝杠、螺母第i个单元受到的轴向力。ΔLsi和ΔLni分别为丝杠和螺母第i个单元的轴向长度,不考虑导程误差时有
ΔLsi=ΔLni=Ph/Z
(1)
式中Ph——丝杠导程
Z——单圈滚道有效承载滚珠数
由赫兹接触理论及标准ISO 3408-4[17]得滚珠丝杠副轴向力平衡方程为
(2)
其中
(3)
(4)
式中Fai——各滚珠所受轴向力
cE——材料常数,对于滚珠的材料轴承钢,取0.464 3
Qi——第i个滚珠与滚道接触点的法向力
δni——第i个滚珠与滚道的法向接触变形量
α——螺母螺旋升角
ck——刚度系数
αi——滚珠与滚道接触角
λ——丝杠螺旋升角
N——有效承载滚珠数
Ys、Yn——丝杠、螺母赫兹接触理论第一类和第二类椭圆积分的辅助值
ρs、ρn——滚珠-丝杠滚道、滚珠-螺母滚道接触点处的曲率半径倒数
rb——滚珠半径
frs、frn——丝杠、螺母滚道适应比
rm——滚珠丝杠公称半径
由图4可得丝杠和螺母第i个单元受到的轴向力为[18]
(5)
丝杠、螺母单元轴向变形量Δsi、Δni为[8]
(6)
式中Es、En——丝杠、螺母弹性模量
As、An——丝杠、螺母横截面积
ΔL——相邻两滚珠之间的丝杠或螺母部分沿轴向的长度
滚珠、螺母受到压力,丝杠受到拉力且三者均发生弹性变形,根据滚珠和丝杠螺母接触关系,把第i、i-1个滚珠,螺母和丝杠轴沿螺旋角方向接触状态放大,如图5所示,可得到滚珠丝杠副第i单元丝杠、螺母、滚珠三者在轴向载荷下变形协调关系
(7)
化简得
(8)
式中δai、δai-1——第i、i-1个滚珠和滚道的轴向接触变形量
整理可得
(9)
化简得
(10)
其中K={[(EsAs)-1+(EnAn)-1]Ph/Z}-1
(11)
图6为第i个滚珠受力变形图,Os、On、Ob分别为滚珠受力变形前丝杠滚道、螺母滚道、滚珠曲率中心,O′n、O′b分别为滚珠受力变形后螺母滚道、滚珠的曲率中心,As、A′s与Bn、B′n分别为滚珠变形前后与丝杠、螺母滚道的接触点,rs、rn分别为丝杠、螺母滚道曲率半径,计算式为
(12)
滚珠的法向变形量与接触角为
(13)
式中α0——初始接触角
1.2 载荷分布结果
对3210型内循环垫片式双螺母滚珠丝杠副进行载荷分析,预紧载荷4 000 N,由于左右螺母受力状态相同,对右螺母进行仿真分析,参数如表1所示。

表1 滚珠丝杠参数
根据国标GB/T 17587.3—2017要求,滚珠丝杠的精度由P1~P5逐渐降低,P5级时有效行程550~630 mm的丝杠对应导程误差为±32 μm,相当于55~63圈滚道的导程误差为±32 μm,平均每圈滚道导程误差ΔPh约为±0.5 μm,相应地,P4~P1级精度对应的导程误差ΔPh分别为±0.4 μm、±0.3 μm、±0.2 μm、±0.1 μm,因此,导程误差ΔPh须在-0.5~0.5 μm范围内进行精度等级划分。
图7、8为各滚珠接触角、接触载荷仿真结果,导程误差直接导致接触角以及载荷分布的不均匀,误差越大分布越不均匀;滚珠丝杠导程误差ΔPh<0时,丝杠滚道与螺母滚道之间的间隙减小,滚珠被挤压,随着滚珠编号的增加,丝杠和螺母滚道之间的偏移越大,滚珠和滚道挤压变形也越大,导致载荷分布呈现上升趋势;ΔPh>0时,丝杠滚道与螺母滚道之间的间隙增加,滚珠变形量减小,随着滚珠编号的增加,丝杠和螺母滚道之间的间隙越大,滚珠和滚道挤压变形越小,载荷分布呈现下降趋势。
表2为滚珠轴向接触变形量总和与丝杠、螺母弹性变形量总和的仿真结果对比,∑δai为滚珠轴向接触变形量总和,∑(Δsi+Δni)为丝杠与螺母弹性变形量总和。
由表2可知,丝杠与螺母弹性变形量总和远小于滚珠轴向变形量总和,占比0.149 0%~0.167 7%,因此,分析滚珠载荷分布时可忽略丝杠、螺母的弹性变形量影响进行简化计算,仿真结果如图9所示。

表2 滚珠轴向接触变形量与丝杠、螺母弹性变形量仿真结果对比
由图9可知,不考虑丝杠、螺母弹性变形以及其他误差时,各滚珠的轴向变形量呈线性分布,且导程误差ΔPh=0时,各滚珠轴向变形量相同。因此,忽略丝杠、螺母弹性变形量计算各滚珠载荷分布情况时,设第1个滚珠变形量为δa1,则各滚珠轴向变形量为
δai=k(i-1)+δa1
(14)
只需计算第1个滚珠的轴向变形量以及各滚珠之间的几何关系即可计算各滚珠的轴向变形量,将极大地简化计算模型,提升计算速度。
2 导程误差与摩擦力矩关系模型
不考虑其他误差影响,滚珠丝杠导程误差ΔPh=0时,各滚珠之间的轴向距离Pa=Ph/Z,根据载荷分布结果,各滚珠受力相等,当垫片厚度使各滚珠与丝杠滚道刚好接触时,此时各滚珠接触变形量为0,预紧力FP0=0,当垫片厚度增加,左右螺母会左右偏移,设偏移量为σa,预紧力为FP,各滚珠受力状态相同,如图10所示。
对单个滚珠的变形量进行分析,如图11所示,σa为螺母滚道曲率中心偏移量,则各滚珠的变形量σn、接触角αP、接触力QP为
(15)
则滚珠丝杠副预紧力为
FP=NQPsinαPcosλ
(16)
如图12所示,当m圈滚道的平均导程误差为ET(ET<0),单一滚道的导程误差为ΔPh=ET/m,则各滚珠之间的导程误差为ΔPa=|ET/(mZ)|以及轴向距离为Pa-ΔPa;设L0为无误差时左右螺母第1颗滚珠的丝杠曲率中心与两螺母中间平面的距离,ΔPh<0时,设第1个滚珠丝杠曲率中心的轴向偏移量为a,则第i个滚珠的丝杠滚道曲率中心的沿丝杠轴线的轴向偏移量为
ΔLi=(i-1)ΔPa+a
(17)
对第i个滚珠的变形量进行分析,如图13所示,ΔPh<0时,滚珠轴向变形量δai为
δai=σa+ΔLicosλ=σa+[(i-1)ΔPa+a]cosλ
(18)
法向变形量δni及接触角αi为
(19)
同理可得,ΔPh>0时
(20)
则滚珠丝杠副预紧力为
(21)
文献[6]提出的摩擦力矩计算模型为
(22)
式中μ——摩擦因数
式(22)将滚珠丝杠副各滚珠受力和接触角视为定值,并未考虑由误差或者变形引起的接触角的变化,使得摩擦力矩计算值与实际存在误差;基于该模型,进行单个滚珠的受力分析,第i个滚珠预紧力与螺母、丝杠的摩擦力矩的关系为
(23)
由于双螺母内的滚珠载荷分布情况相同,则丝杠副的摩擦力矩为两个螺母摩擦力矩之和,即
(24)
综上所述,滚珠丝杠副导程误差与摩擦力矩的关系模型为
(25)
通过计算以及查找厂家手册可知,垫片刚度为75 000~85 000 N/μm,滚珠丝杠副的轴向预紧力为3 000~6 000 N,则由轴向预紧而导致的垫片弹性变形量为0.035~0.08 μm,远小于滚珠变形量,在此忽略不计,因此,相同型号且垫片厚度相同的双螺母滚珠丝杠副其螺母滚道曲率中心偏移量σa相等,同时,螺母与垫片直接接触,则左右螺母的滚道曲率中心偏移量σa不会随着滚珠丝杠的导程误差发生变化。
3 试验与结果分析
3.1 试验台
为了验证本文的模型,通过滚珠丝杠副行程误差、摩擦力矩试验台测量导程误差以及摩擦力矩。图14为滚珠丝杠副行程误差试验台,该试验台由伺服电机、气浮工作台、激光位移传感器和圆光栅组成。伺服电机驱动丝杠旋转,工作台由气浮支撑,可沿轴向无阻力平稳移动,工作台安装有可与丝杠滚道啮合的球形测量头。丝杠旋转带动工作台轴向移动,激光位移传感器通过采集工作台的轴向位置测量丝杠的实际轴向位置,而圆光栅通过采集丝杠的角度位置变化计算出丝杠的理论轴向位置,实际轴向位置与理论轴向位置的差值即为丝杠导程误差。
图15为滚珠丝杠副摩擦力矩试验台,该试验台由伺服电机、工作台、一对滚动直线导轨和力传感器组成。伺服电机驱动丝杠旋转,工作台装有可与丝杠滚道啮合的支撑座,使丝杠在无附加力的条件下带动工作台沿直线导轨轴向移动。滚珠丝杠副螺母法兰装有螺栓,伸出法兰端面的螺栓与力传感器接触,通过软件计算得到滚珠丝杠副的摩擦力矩。
3.2 试验流程
图16为试验流程图,在不安装螺母的情况下,测量一系列不同精度等级丝杠的导程误差,将各丝杠分别匹配同一套螺母、垫片、滚珠组成丝杠副,更换丝杠而不更换螺母、垫片、滚珠,根据ISO(3408—5:2006)测量各丝杠与螺母组成丝杠副的摩擦力矩,丝杠、螺母、滚珠、垫片相关参数如表3所示。
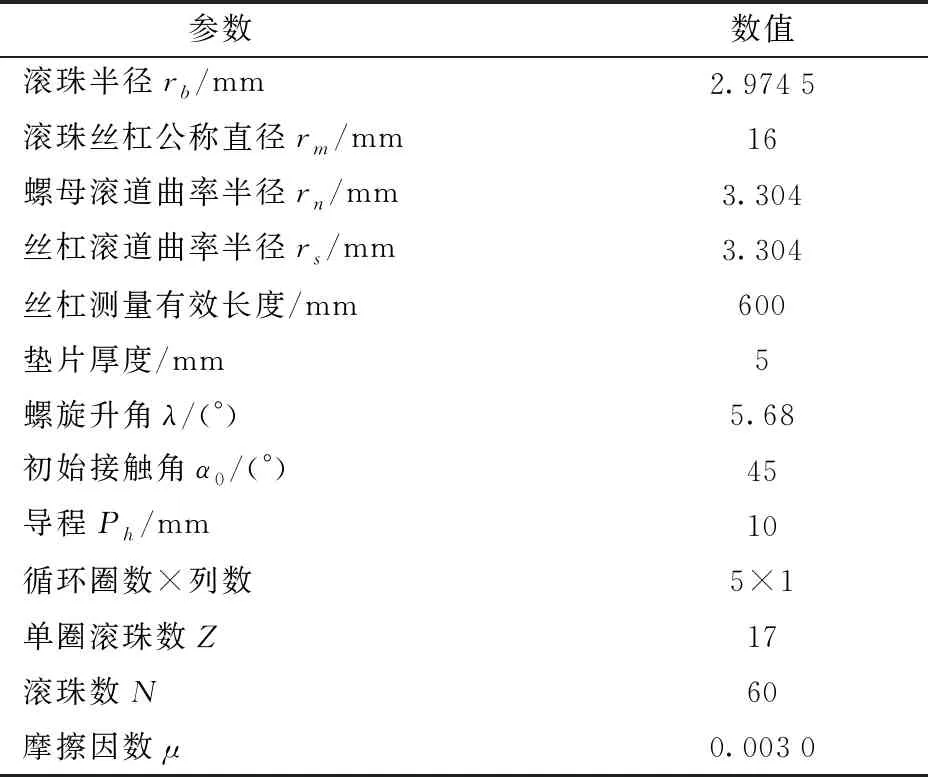
表3 丝杠、螺母、滚珠、垫片参数
常温下丝杠的导程误差一般都小于0,在实际加载工况下,不同加工精度的丝杠在一定温升之后会存在热伸长导致导程误差大于0;但由于行程误差和摩擦力矩试验台需在20℃恒温条件下完成测量,无法针对热伸长后的丝杠进行测量,因此,考虑到试验的可操作性,本文只对导程误差小于0的多种情况进行验证分析。
3.3 试验结果与分析
存在导程误差时,螺旋升角为
λ′=arctan((Ph+ΔPh)/(2πrm))
(26)
本次试验中,测得滚珠丝杠副导程误差ΔPh为-0.612 3~-0.128 7 μm,则螺旋升角变化范围为5.680 3°~5.680 5°,变化微小,忽略螺旋升角的变化。
根据滚珠丝杠的导程误差及摩擦力矩可求出左右螺母的滚道曲率中心偏移量σa,σa不会随着导程误差的变化而变化;第1颗滚珠接触位置的丝杠曲率中心距离两螺母中间平面的轴向偏移量a为第1个滚珠接触的丝杠滚道曲率中心距离两螺母中间平面的滚道数n与导程误差的乘积,即a=nΔPh,设a1=σa+acosλ,则此时滚珠法向变形量与接触角为
(27)
当垫片厚度一定时,滚道数n不发生变化,则a、a1与导程误差呈线性关系。根据试验结果计算a1,如图17所示,经直线拟合得:a1=2.569ΔPh+3.187,则试验丝杠组成的丝杠副第1颗滚珠的轴向偏移量a=2.569ΔPh/cosλ=2.582ΔPh,螺母滚道曲率中心偏移量σa=3.187 μm。
表4为摩擦力矩、预紧力的试验数据与理论计算数据对比,各丝杠的导程误差均小于0,摩擦力矩的理论计算值与试验值的相对误差不大于8.79%,理论模型与实际摩擦力矩的一致性较好。

表4 摩擦力矩和预紧力试验数据与理论计算数据
图18、19分别为摩擦力矩、预紧力与导程误差关系曲线。由图18、19可知,通过本文模型计算的预紧力、摩擦力矩更接近试验测量值,而文献[6]的计算值与试验测量值相差较大;结合表5,文献[6]模型计算的摩擦力矩误差为11.75%~54.69%,而本文模型计算摩擦力矩的相对误差范围为0~8.79%,表明计算摩擦力矩时,未考虑导程误差以及滚珠变形引起的接触角变化,且将各滚珠视为受力相同,会产生较大误差。
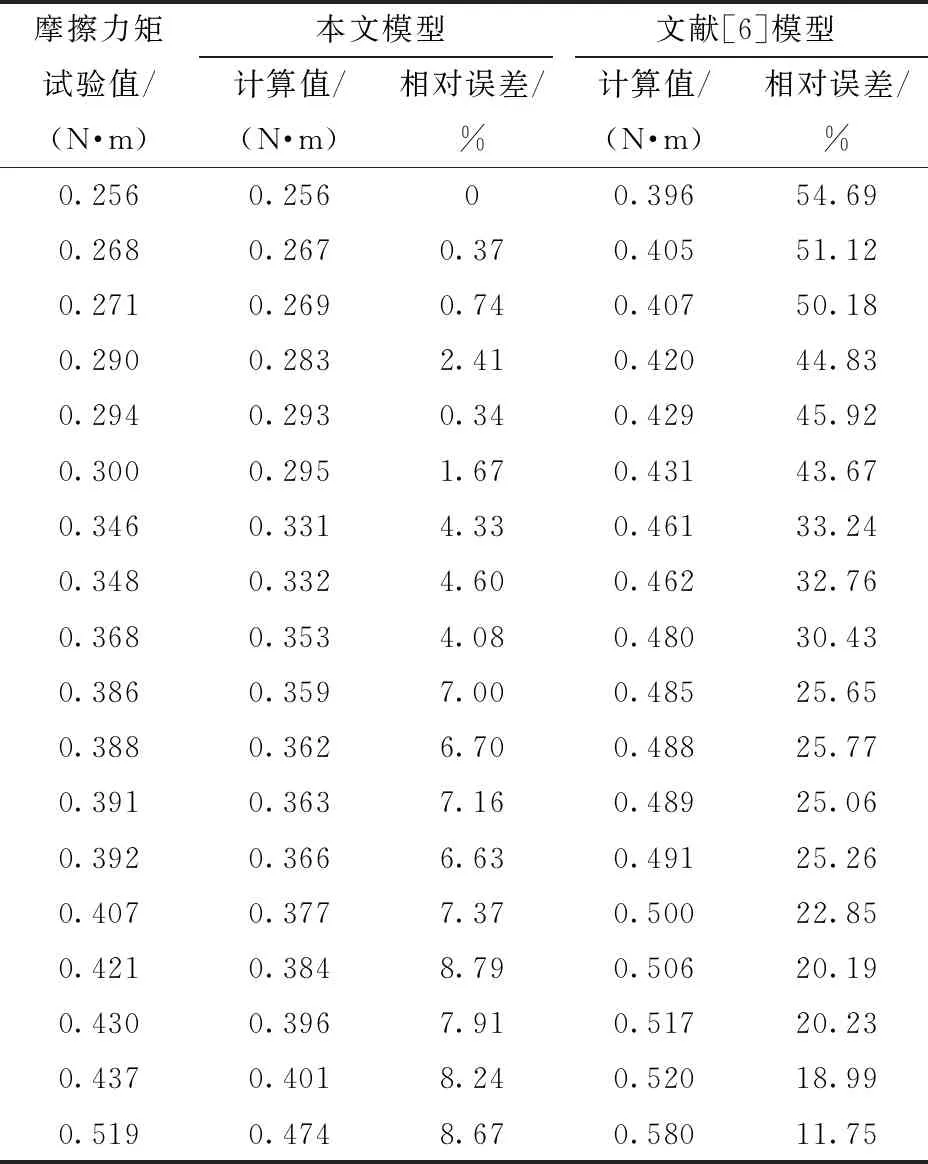
表5 本文模型、文献[6]模型计算摩擦力矩相对误差对比
综合对比表4、5以及图18、19,双螺母滚珠丝杠副的预紧力以及摩擦力矩均会随着导程误差的增加而加大,且近似于线性相关。本文理论计算的摩擦力矩值与测量值之间的相对误差随着导程误差的增加而增加,而文献[6]则呈相反趋势。这是由于滚珠的接触角随着导程误差的增加而减小,摩擦力矩随着接触角的减小而增大,但由于丝杠螺母存在弹性变形,使得本文模型计算的接触角与实际值存在偏差,丝杠导程误差越大,丝杠螺母弹性变形量越大,接触角计算值与实际值差值越大,导致本文模型的摩擦力矩计算值与试验值的相对误差出现增大的趋势;而文献[6]计算摩擦力矩时,将各滚珠的接触角视为常数45°,导致摩擦力矩计算值与导程误差的斜率小于试验值与导程误差的斜率,使得文献[6]摩擦力矩计算值相对误差出现减小的趋势。但是依据国标GB/T 17587.3—2017,滚珠丝杠副导程误差允许值在-0.500 μm以内,因此本文模型的相对误差最大值为8.79%,优于文献[6]模型,验证了本文模型的有效性。
4 结论
(1)通过对只承受预紧载荷的双螺母滚珠丝杠副进行载荷分布分析发现,导程误差直接导致接触角、载荷分布的不均匀,误差越大,分布越不均匀;滚珠丝杠导程误差小于0时,丝杠滚道与螺母滚道之间的间隙减小,滚珠被挤压,滚珠编号递增,丝杠和螺母滚道之间的偏移越大,滚珠和滚道挤压变形也越大,导致载荷分布呈上升趋势;导程误差大于0时,载荷分布呈下降趋势。
(2)在不考虑丝杠、螺母弹性变形及其他误差时,各滚珠的轴向变形量呈线性分布,只需计算第1个滚珠的轴向变形量和各滚珠之间的导程误差即可得出各滚珠的轴向变形量,进而计算预紧力与摩擦力矩。
(3)双螺母滚珠丝杠副左右螺母的滚道曲率中心轴向偏移量σa与垫片厚度有关,第1个滚珠接触的丝杠滚道曲率中心至两螺母中间平面的轴向偏移量a与导程误差线性相关,σa与a可通过导程误差与摩擦力矩拟合求出。
(4)试验表明,摩擦力矩与导程误差呈线性关系,摩擦力矩实际值大于理论计算值,这主要因为螺母内滚道导程误差使滚珠的变形量较计算值偏大,摩擦力矩理论值与实际值相对误差不大于8.79%。
(5)对比本文模型和文献[6]模型发现,文献[6]模型摩擦力矩计算值的相对误差范围为11.75%~54.69%,而本文模型摩擦力矩计算值的相对误差范围为0~8.79%,相对误差明显减小。这表明在计算摩擦力矩时,不考虑导程误差和滚珠变形引起的接触角变化,且将各滚珠视为受力相同,会产生较大误差,从而验证了本文模型的有效性。

