核心素养视角下的数学测评研究

农桂香 李映辉 王守峰

摘 要：本文以2021年八省联考数学试题为例，基于喻平教授提出的数学核心素养评价框架，剖析了试卷中的数学核心素养分布。通过对试题的研究发现：2021年新高考八省联考数学试题在2020年新高考数学试卷的基础上，有较大的创新，总体上对学生的数学核心素养提出了更高的要求，但试题对数学建模和数据分析素养的考查有待进一步加强。

关键词：新高考;数学测评;数学核心素养

1 问题提出

教育部在2014年3月发布的《关于全面深化课程改革，落实立德树人根本任务的意见》中明确提出落实课程改革的关键领域和主要环节是研究制订学生发展核心素养体系和学业质量标准、修订课程方案和课程标准、改进学科教学的育人功能[1]。2016年9月，教育部公布《中国学生发展核心素养》，正式确定学生发展核心素养的框架、维度和指标[2]。紧接着，教育部在2018年1月印发的《普通高中数学课程标准（2017年版）》中将数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析作为数学学科核心素养的六大成分，这是新课标对学科核心素养的一次凝练[3]。随着课程改革的不断深入，越来越多的研究者把关注点放在了学生数学学科核心素养的评价和发展上。2019年11月教育部考试中心颁布的《中国高考评价体系说明》强调了学科素养在高考考查中的导向作用[4]。当前，数学学科核心素养已经成为数学教育研究的热点，而数学核心素养的测评是数学核心素养研究的关键。

数学学习评价的一个重要内容是数学核心素养的评价，目前影响最大并且应用最广泛的评价模型有PISA测试、SOLO分类理论和布鲁姆的学习评价模型。喻平教授在文献[5]中对上述三个评价模型进行了分析，指出数学知识学习表现为知识理解、知识迁移、知识创新三种形态。在喻平教授数学核心素养评价理论的指导下，许多学者对高中数学测评试卷进行了数学核心素养的考查分析[67]。

2019年4月，我国第三批实施高考综合改革方案的8个省市正式向外界发布了最新的高考改革方案，并在该方案的指导下，产生了八省联考。目前，八省联考数学试题在全国范围内已有一定影响。本文以喻平教授的理论框架为指导，对2021年八省联考数学试题中数学核心素养的考查情况及考查特点进行研究。

2 数学核心素养考查情况分析

2021年八省联考数学试题主要考查了函数、导数、平面向量、三角函数、数列、立体几何、解析几何、概率统计等知识点。试卷共有22道考题，其中1～8题为单项选择题，9～12题为多项选择题，13～16题为填空题，17～22题为解答题。本节将对该试卷中数学核心素养的考查内容特点进行分析。

2.1 试题中数学抽象素养的考查分析

数学抽象素养是指通过对数量关系与空间形式的抽象，得到数学研究对象的素养[3]。

第8题：已知a<5且ae5=5ea，b<4且be4=4eb，c<3且ce3=3ec，则（ ）。

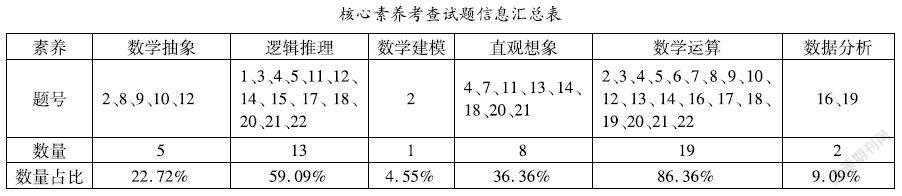
A.c

核心素养考查分析：本题考查的知识点是用导函数求函数单调性和比较函数值的大小。为了解决该题，学生需要仔细观察题目给出<的代数式，找出其特点，并抽象出函数H（x）=exx，对H（x）=exx求导得出函数单调性，就可以比较大小。该题的关键在于将ae5=5ea，be4=4eb，ce3=3ec这三个式子分别转化成e55=eaa，e44=ebb，e33=ecc构造函数H（x）=exx，得到函数模型，用具体思想方法得出结果。

2.2 试题中逻辑推理素养的考查分析

逻辑推理素养是指从一些事实和命题出发，依据规则推出其他命题的素养。主要包括两类：一类是从特殊到一般的推理，一类是从一般到特殊的推理[3]。

第3题：关于x的方程x2+ax+b=0，有下列四个命题：

甲：x=1是该方程的根  乙：x=3是该方程的根

丙：该方程两根之和为2 丁：该方程两根异号

如果只有一个为假命题，则该命题是（ ）。

A.甲 B.乙 C.丙 D.丁

核心素养考查分析：本题考查了对真假命题的判断，学生要根据二次函数根与系数的关系来对甲、乙、丙、丁四个选项进行判断。因为四个命题中只有一个为假命题，所以要对四个命题进行组合。对于甲、乙、丙这三个命题，由于这三个命题不能同时成立，故假命题在甲乙丙中;对于甲、乙、丁这三个命题，由于这三个命题不能同时成立，故假命题在甲乙丁中;对于甲、丙、丁这三个命题，由于这三个命题不能同时成立，故假命题在甲丙丁中。綜上所述，假命题为命题甲。该题以二次函数根与系数的关系为背景，探究并判断命题真假，从而进行逻辑的表达与交流，对学生的逻辑推理素养的考查落到了实处。

2.3 试题中数学建模素养的考查分析

数学建模素养是对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的素养[3]。

第2题：在3张卡片上分别写上3位同学的学号后，再把卡片随机分给这三位同学，每人1张，则恰好有一位学生分到写有自己学号卡片的概率为（ ）。

A.16 B.13 C.12 D.23

核心素养考查分析：该题以实际问题中的“分配问题”为背景，考查了排列知识。学生需要在理解题目的前提下，把这个生活中的实际问题转化成一个抽象的数学问题，而这个数学问题需要用排列知识解决，建立起一个数学模型，并写出解答过程：1-1+2A33=12。这里1+2A33的分子中1表示三位学生都分到写有自己学号卡片的情况有1种，2表示三位学生都没有分到写有自己学号卡片的情况有两种。但是有些学生在对实际问题进行数学抽象，从而构建数学模型的过程中会遇到不同程度的障碍。

2.4 试题中直观想象素养的考查分析

直观想象素养是指借助几何直观和空间想象感知事物的形态与变化，利用空间形式特别是图形，理解和解决数学问题的素养[3]。

第13题：圆台上、下底面的圆周都在一个直径为10的球面上，其上、下底面半径分别为4和5，则该圆台的体积为（ ）。

核心素养考查分析：本题考查了外接球问题和圆台的体积公式，对学生的直观想象素养提出了一定的要求。学生首先要根据题目信息进行空间想象，画出相应的直观图，确定圆台上下底面与球面半径的关系，再根据几何关系求出圆台的高度，最后根据圆台的体积公式V=13πh（R2+r2+R·r）即可得出本题的答案。

2.5 试题中数学运算素养的考查分析

数学运算素养是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养[3]。

第6题：（1+x）2+（1+x）3+…+（1+x）9的展开式中x2的系数是（ ）。

A.60 B.80 C.84 D.120

核心素养考查分析：本题考查二項式相应项的系数之和，需要学生灵活运用组合公式Cm-1n+Cmn=Cmn+1进行运算。要求学生具备一定的数学运算求解能力。据二项式定理可知（1+x）2+（1+x）3+…+（1+x）9的展开式中x2的系数为：

C22+C23+C24+…+C29=C33+C23+C24+…+C29

=C34+C24+…+C29

=…

=C310

=120

本题的关键在于灵活运用组合公式进行计算。

2.6 试题中数据分析素养的考查分析

数据分析素养是指针对研究对象获取数据，运用数学方法对数据进行整理、分析和推断，形成关于研究对象知识的素养[3]。

第19题：一台设备由三个部件构成，假设在一天的运转中， 部件1、 2、 3需要调整的概率分别为0.1、0.2、0.3，各部件的状态相互独立。

（1） 求设备在一天的运转中，部件1、2至少有一个需要调整的概率;

（2）记设备在一天的运转中需要调整的部件个数为X，求X的分布列和数学期望。

核心素养考查分析：该题以设备调整这一生活情境为问题背景，渗透了对数据分析素养的考查。为了解决该题，要求学生能够利用对立事件概率公式求解以及根据离散型随机变量的概念求分布列和数学期望。

对于第一小问，题目要求求出部件1、2至少有一个需要调整的概率。学生可以采用两种方式进行解题。部件1、2至少有一个需要调整的概率意味着有三种情况：部件1需要调整，部件2不需要调整;部件1不需要调整，部件2需要调整;部件1需要调整，部件2需要调整。则部件1、2至少有一个需要调整的概率：

P=0.1×（1-0.2）+（1-0.1）×0.2+（1-0.1）×（1-0.2）

=0.28

除了采用直接的方法来进行求解，还可以先求出部件1、2都不需要调整的概率，再用1减去所求得的概率即为部件1、2至少有一个需要调整的概率。

对于第二小问，分布列和数学期望的求法有一个较为固定的解题方式，解题的关键在于将调整的部件个数X一一列出来，再根据数学期望公式计算求解。

本节的最后，我们将每道题的素养考查情况列成下表。

从上表中的数据中可以发现，2021年八省联考数学试题对六大数学核心素养均有不同程度的考查。其中对数学运算素养的考查比重最大，其次是逻辑推理素养，数学建模和数据分析素养考查的试题较少。此外，多个题目考查了多种核心素养。

3 结论与建议

通过对2021年八省联考数学试题中数学核心素养考查情况的具体分析，可以得到如下结论：

在核心素养考查情况上，2021年八省联考数学试题以数学学科知识为载体，强化了对数学学科核心素养的综合考查。试卷中有多个试题都涉及了多种素养的考查。但数学建模和数据分析的考查力度需要进一步加强。

在题型结构上，本次试卷打破了以往试卷结构的固定形式，增加了开放题和创新性试题。开放题体现在第15题，题目要求写出最小周期为2的奇函数，这道题目的答案有很多种，考查学生平时的数学积累。创新试题体现在第20题，该题以北京大兴国际机场空间弯曲性为背景，考查了高中数学立体几何方面的知识，该题打破了固有的形态，直接给出关于曲率的定义，学生需要在读懂定义的前提下去解题。

在知识内容上，出现了学科和跨学科综合性试题。此次考试中不仅出现了数学学科综合试题，如第12题，该题是三角函数和导函数的综合试题，还出现了跨学科试题，如第16题，是物理学科与数学学科相融合的试题。这两道试题体现了学科与学科之间大融合的理念，对学生的综合素养提出了较高的要求。

另一方面，为了解决新高考中对数学核心素养考查存在的问题，基于前面核心素养考查的具体分析，提出以下几点建议：

命题应适当增加试题对学生数学建模和数据分析的考查比例。数据分析作为一门重要的数学技术，主要用于随机现象的研究，成为大数据时代数学应用的一个主要方法。而数学模型作为一座桥梁，搭建了数学与外部世界的联系，是数学应用的重要形式。数据分析和数学建模素养作为六大数学核心素养的两大重要组成部分，在培养学生获取信息和处理数据能力，提升逻辑推理能力等方面起到至关重要的作用。因此，加强这两大核心素养的考查力度是必要的。

教师要培养学生的开放性思维。高考试题中出现开放性试题是未来高考的命题导向。作为一线教师应该转变自身的数学教育教学方式，培养学生的发散思维。各类模拟考试也应适应这一趋势，加强以开放性问题为载体的数学核心素养的考查。

数学教师在教学过程中要注重数学与其他学科之间的交叉性与融合性。在数学的教学当中适当融入其他学科的知识，这不仅有利于培养学生的学科融合意识，还对学生的学科核心素养的持续发展有很大的促进作用。各类高考模拟考试应该强化以跨学科问题为依托的数学核心素养的考查。

参考文献：

[1]中华人民共和国教育部.关于全面深化课程改革，落实立德树人根本任务的意见[EB/OL].基教二[2014]4号.

[2]核心素养研究课题组.中国学生发展核心素养[J].中国教育学刊，2016（10）：13.

[3]中华人民共和国教育部.普通高中数学课程标准（2017年版）[M].北京：人民教育出版社，2018：48.

[4]教育部考试中心.中国高考评价体系说明[M].北京：人民教育出版社，2019：2930.

[5]喻平.数学核心素养评价的一个框架[J].数学教育学报，2017，26（2）：1923.

[6]覃创，严忠权.核心素养为导向的数学测评研究——以2019年高考全国Ⅲ卷为例[J].数学教育学报，2020，29（02）：2428.

[7]李爽，杨泽恒，王彭德.核心素养视角下云南高中学业水平考试和高考数学试卷分析[J].数学教育学报，2020，29（06）：2531+91.

基金项目：云南师范大学本科线下一流课程建设项目（2019xxkc28）

作者简介：农桂香（1997— ），女，壮族，广西靖西人，硕士，研究方向：学科教学（数学）。

*通讯作者：王守峰（1979— ），男，汉族，山东济南人，博士，教授，研究方向：学科教学（数学）、代数。