补偿法解题初探

云南 王子谦

补偿法是一种有效的解题方法，但高中物理对补偿法的介绍却比较少，学生对微元法、整体法、隔离法了解和应用得较多。由于补偿法本身具有灵动跳跃、思维敏捷的特点，学生较难掌握，因此在高中阶段介绍不多，教师在课堂上慢慢道来却另有一番风味，下面我们作一些有益的尝试。

1.力学中的补偿法

伽利略的很多实验都是“天才”之作，最美丽的十大物理实验伽利略就占了两个：“伽利略的自由落体实验”和“伽利略的加速度实验”，这两个实验都是神来之笔，其中“伽利略的自由落体实验”就是以上所说的补偿法的具体表现。

具体内容是这样的：当时人们普遍认为从同一高度自由下落的重球先落地，轻球后落地。伽利略就设想把轻球和重球连在一起，此时连接体变成一个更重的球，这个球应比原来两个球更快落地，但连接体中轻球会牵扯重球，重球的速度将减慢，这样连接体下落的反而比重球还慢。伽利略利用这一矛盾驳斥重球先落地、轻球后落地的结论。从这一论证过程看，伽利略是做了一个条件补偿后得到另一结论来否定原结论的。

补偿法在力学中的应用还有：求被挖掉一个小圆的大圆薄板的质心；求不规则物体的转动惯量；求重力矩；求不规则物体之间的万有引力等。

2.电学实验中的补偿法

采用伏安法测未知电阻时，通常的实验方法会因电压表分流给测量结果带来误差。在伏安法测电阻中要想进一步减小电压表内阻对测量结果的影响，可采用电流补偿法。假设增加一个电源并组成如图1虚线框中的电路，Rx与电压表V有一端直接连在一起，另一端通过开关K2和检流计G连在一起。调节R1使电压表中电压值恰与待测电阻Rx两端的电压相等时，流过检流计G的电流为零，这时无论电压表内阻大小如何，都不会影响被测量电路中的电流，从而达到精确测量的目的，这种方法就叫电流补偿法。

图1

3.交变电流中的补偿法

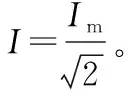
假设有两个交变电流，其电压变化规律如图2所示，它们的最大值与周期都相同，它们的瞬时表达式分别为u1=Umsinωt、u2=Umcosωt，把它们分别加在两个阻值相同的电阻上，设电阻的阻值为R，在一个周期内两个交流电产生的焦耳热相同，都为Q，产生的总的焦耳热Q总=2Q。设它们交流电压的有效值为U，则有：

另外，在任一时刻t，这两个电阻上的热功率分别为：

两个电阻上总的发热功率为：

可以看出，两个电阻上发热的总功率是定值，与时刻t无关，所以在一个周期内两个电阻上总的发热量为：

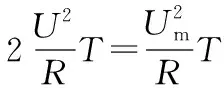
把正弦交流电和余弦交流电巧妙地结合在一起，起到一个化变为不变的效果，把原来需要高深数学知识才能解决的问题化解为简单问题。

4.在物理竞赛中使用补偿法

在物理竞赛试题中利用补偿法能取得意想不到的效果，能让学生感受到巧妙的构思。

【例2】如图3所示，A1A2是面积很大、互相平行又相距较远的带电金属板，相距为d，两板间的电势差为U。同时，在两板间还有方向与匀强电场正交且垂直纸面向外的均匀磁场。一束电子通过左侧带负电的板A1上的小孔，沿垂直于金属板的方向射入，为使该电子束不碰到右侧带正电的板A2，问所加磁场的磁感强度至少多大?设电子所受重力及从小孔进入时的初速度均可不计。

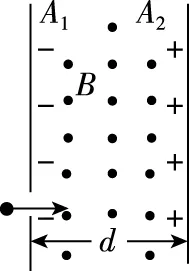
图3

【分析】电子在复合场中仅受两个力，即电场力和洛伦兹力，由于洛伦兹力为变力，故合力亦为变力。该变力大小及方向均在随时间变化，故运动既非匀变速运动，也不是匀速圆周运动或简谐运动。这里我们就可用补偿法解题，首先设想一个力F1来平衡电场力以消除电场力F2引起的电子速率变化，将问题简化，然而添加一个力后必须要另加一个反向的力才能和原来的运动效果完全相同，我们可以设电子沿y轴有大小相等方向相反的初速度，其合速度仍为0，其中一个分速度对应的洛伦兹力平衡掉电场力，运动情境就变为有初速度且仅受一个洛伦兹力的情况了。

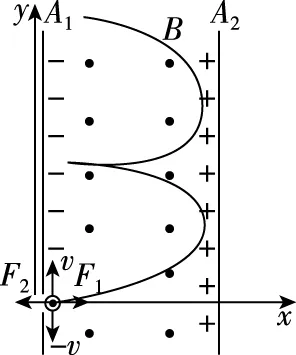
图4

图5

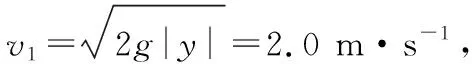
5.应用补偿法的易错点

虽然补偿法能够将复杂的问题变得简单，但不是所有情况都能使用补偿法来解决，如在电磁感应问题中，如果在分析问题时考虑的不够全面，就很容易出现错误。

【例3】一正方形线框以速度v1进入一有界匀强磁场区域，线框边长L，磁场宽度也为L。线框电阻R，磁感强度为B，求线框离开磁场时的速度v2。

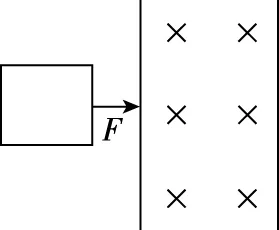
图6

【错解】这道题中的线框通过匀强磁场区域时受变力作用而做非匀变速运动。如果采用补偿法解题，假设线框进入匀强磁场区域时受一恰与此时安培力相等的恒定外力作用，线框就可匀速通过该磁场区域。在此过程中F做功W=2FL，这一过程跟不受F力作用时差异在于F力的功保证了动能不变，所以有如下解答。

造成错解的原因是对问题的分析不够全面，造成补偿后运动过程中的安培力变大，产生的焦耳热增加，补偿之后条件已经改变，所以由此计算出的结论是错误的。因此使用补偿法时要谨慎。