2021年高考全国乙卷物理第25题解法探析

宁夏 朱巧萍 张永刚

1 真题呈现

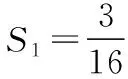
(1)金属棒在磁场中运动时所受安培力的大小；

(2)金属棒的质量以及金属棒与导体框之间的动摩擦因数；

(3)导体框匀速运动的距离。

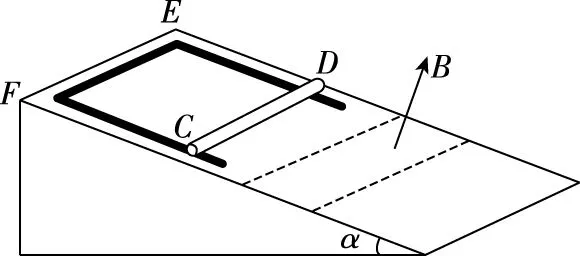
图1

2 考题解析

此考题属于“动力学+电磁学”的综合性试题，共分为三个小问题，涵盖物理学科核心素养的四个维度，随着考查维度的变化，问题难度不断提升，但是难易程度的层次分明，具有很好的选拔功能。从高考试题的作用来看，此考题很好地体现了高考试题从“考知识”向“通过知识考查能力”的转变，特别是通过对分析能力、运算能力、推理能力、模型建构能力的考查，来检测学生科学思维中模型建构、科学推理、科学论证、质疑创新等要素，彰显出高考试题对学生物理学科核心素养发展水平的全面系统、深入综合的测试意图。

考题以“匀强磁场中导体切割磁感线运动”的问题情境为载体，通过三个物理过程给出考题的全部信息和隐含条件。为了便于研究和分析考题，现将三个物理过程分析如下，其中金属棒CD和导体框EF分别用CD和EF予以代替。

2.1 第一个物理过程(CDEF匀加速直线运动过程)

2.2 第二个物理过程(CD匀速EF匀加速运动过程)

设CD的质量为m，CD与EF间的滑动摩擦力及其动摩擦因数分别为f和μ，EF的加速度为aEF，CD受到的安培力为FCD。CD以v1=1.5 m/s的速度进入磁场并匀速运动；同时EF以v1=1.5 m/s的初速度，做加速度为aEF的匀加速直线运动。CD和EF间的滑动摩擦力为f=μmgcosα；运用右手定则(或楞次定律+右手螺旋定则)和左手定则，可知CD上的感应电流方向由D到C(即垂直纸面向外)，FCD的方向沿斜面向上。对CD受力分析如图2所示：

图2

因EF沿斜面向下匀加速运动(CD所受滑动摩擦力的方向沿斜面向下)且CD匀速运动，则有：

mgsinα+μmgcosα=FCD(1)

2.3 第三个物理过程(CD加速EF匀速运动过程)

设CD的加速度为aCD，EF匀速运动的速度为v2，所受安培力的大小为FEF，方向沿斜面向上，磁场的宽度为D，EF在磁场中匀速运动的距离为d。

当CD以速度v1离开磁场的瞬间，EF正好以速度v2进入磁场，分析EF从v1到v2的匀加速运动过程可知：

EF进入磁场后匀速运动(EF受滑动摩擦力的方向沿斜面向上)，EF受力分析如图3所示：

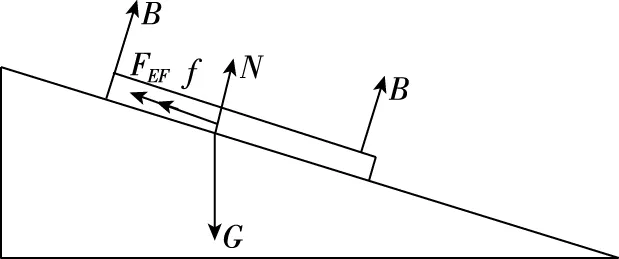
图3

则有：Mgsinα-μmgcosα=FEF(2)

在线框进入磁场前，设线框所受合力为F合

F合=Mgsinα-μmgcosα=FEF

由(2)式和(3)式可得关系式：aEF=2 s-1×v2；

可以求得：v2=2.5 m/s；aEF=5 m/s2。

将f代入(1)式可求得：

3 第三个小问题的三种解法

考题的前两个小问题，考生可以通过对重力、安培力、滑动摩擦力进行受力分析，围绕速度、位移、加速度的关系，采用运动学公式、动能定理、动量定理等多种方法进行求解。但是，考题的第三个小问题就需要考生运用模型思维进行求解，考查学生分析判断、严谨认真的思维品质和科学态度。

3.1 基于模型思维分析错误解法

关于考题的第三个小问题(求解EF匀速运动的距离)，常见的错误解法有：

错解1：设CD离开磁场匀加速运动的时间为t2，EF匀速运动的距离为d，求出CD的加速度

aCD=gsinα+μgcosα=9 m/s2

由此可得：

错解2：CD向下匀加速运动，EF在磁场中匀速运动，当二者共速时EF不再匀速，则有：

定义7 设X为一非空集合，υ1=(A1,λ1),υ2=(A2,λ2)是定义在X上的两个智立方集，则υ1和υ2之间的可能度公式为

错解3：对CD进行受力分析，对其运用动量定理求解：

错误的原因是没有对CD和EF的受力与运动状态进行深入分析，然后再做出判断。简言之，没有判断EF匀速运动的距离d与磁场宽度D之间的关系，就理所当然地认为EF的匀速运动和匀加速运动都发生在磁场中，这是错误的。这样的解法缺少严谨认真的科学态度和科学思维中的科学推理、科学论证的判断环节。

考题原文“当金属棒离开磁场的瞬间，导体框的EF边正好进入磁场，并在匀速运动一段距离后开始加速……”，这样的表述并没有明确地说明EF的匀速运动和随后的加速运动是发生在磁场中还是磁场之外，所以，上述解法都是不科学、不严谨的。其实，考题是有意地以这样的文字表述，考查学生科学推理和科学论证的严谨性。因此，在解答第三个小问题时应该先判断磁场宽度D和EF匀速运动距离d之间的关系。

物理模型建构是科学思维的重要组成部分，模型进阶的过程正是科学思维发展的过程。建构物理模型的目的是对研究对象进行抽象，理解物理现象中所包含的科学思维，进而运用模型思维解决问题，即模型思维是运用已有的和已知的物理模型解决问题的思维方式。在运动学中非常典型的一个问题模型是“刹车问题陷阱模型”，这个问题模型与考题中第三个小问题的模型极其相似，可谓是“异曲同工”。

图4

3.2 受力分析法

根据CD的受力可知，EF匀速运动的距离d取决于磁场宽度D和CD的受力情况，当EF以v2=2.5 m/s的速度在磁场中匀速运动，同时CD以v1=1.5 m/s的初速度离开磁场，开始匀加速运动。由二者间摩擦力f的方向可知：

当f沿斜面向下时，则有maCD=mgsinα+μmgcosα，解得：aCD=9 m/s2；

当f=0(即二者共速没有摩擦力)时，则有maCD=mgsinα，解得：aCD=6 m/s2；

当f沿斜面向上时，则有maCD=mgsinα-μmgcosα，解得：aCD=3 m/s2；

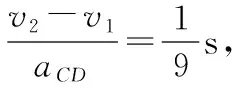
(2)如果D=d，则EF匀速运动的距离等于磁场的宽度D，说明磁场中仅存在着匀速运动的状态。EF离开磁场后不再受到沿斜面向上的安培力和滑动摩擦力的作用，CDEF整体仅在重力和支持力的作用下共同加速运动，EF也符合题意“匀速运动一段距离后开始加速”的运动状态。

综上分析可知，在磁场宽度足够的条件下，EF匀速运动的距离取决于滑动摩擦力的作用时间。当磁场宽度不足时，如果按照滑动摩擦力存在的时间来求解EF匀速运动的距离，显然就是错误的。

3.3 图像对比法

上述的受力分析法需要详细地分析物体的受力情况，然后再分情况讨论，解题过程显得繁琐。其实，将此问题视为两个物理过程更为简洁，即开始时CD匀速运动、EF匀加速运动和结束时EF匀速运动、CD匀加速运动的两个过程，再根据速度位移关系即可求解。

设：CD离开磁场做加速度aCD=9 m/s2的匀加速直线运动，运动位移为dCD，时间为t2；磁场宽度足够大，EF的匀速运动完全发生在磁场中，绘制两个运动过程的速度时间(v-t)图像如图5所示。根据图5可以得出图6所示的，能够表示EF与CD的速度位移关系(a)式和(b)式。

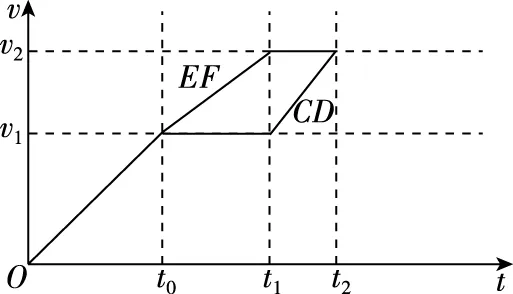
图5

图6

3.4 能量转化法

如果把CDEF视为一个整体，运用能量守恒定律通过一个物理过程来求解，可使解题思路更为简洁。先分析滑动摩擦力做功及其产生的摩擦热，CD和EF间两次的相对滑动位移求解过程如下：

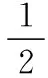
考题中安培力做功是将一部分重力势能转化为电能，滑动摩擦力所做的功数值上等于产生的摩擦热，也会损耗一部分重力势能。将整个过程视为重力、滑动摩擦力、安培力做功的过程，运用能量守恒定律和功能关系可以列出如下的方程式：Wg+Wf+WFCD+WFEF=ΔEk

重力对CDEF系统做功为Wg；滑动摩擦力对系统做功为Wf；安培力做功分别为WFCD和WFEF；系统动能变化为ΔEk。

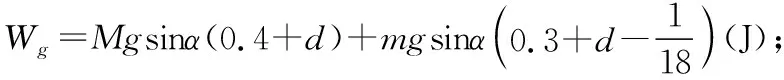
解题过程如下图所示：

图7

4 结束语

由概念和规律构成的物理观念是人脑对物理知识及其结构的升华和概括。高考试题综合性比较强，每一道试题要考查多个物理概念和规律，通过挖掘高考试题考查概念规律之间关联和进阶关系，可以让学生深刻理解概念和规律，由知识网络和进阶关系构建物理观念。此考题所涉及的物理观念包括：含有速度位移关系的运动观念；含有受力分析的相互作用观念；含有楞次定律、安培力做功、功能关系的能量转化观念。可谓是全面、深入、综合地考查了学生的物理观念。

观察、实验与科学思维相结合，是物理学科的基本特征，科学思维是具有意识的人脑对科学事物的本质属性、内在规律及事物之间的相互联系和关系的间接与概括的反映，是物理学科核心素养的核心内容。科学思维能力更是物理学科的灵魂所在，认识、解读和运用物理规律多角度、深层次、全方位地发现问题、分析问题和解决问题更应该是科学思维的一种体现和要求。此考题突出地考查了学生科学思维能力的发展水平，这为今后高中物理教育教学的核心工作指明了方向。