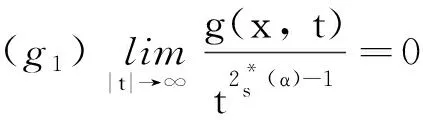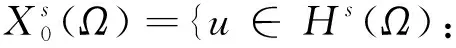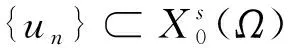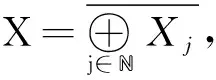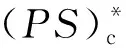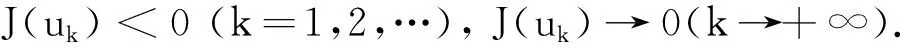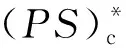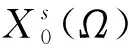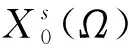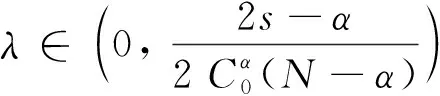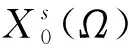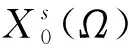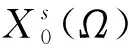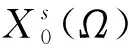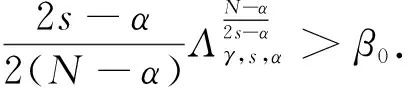一类分数阶奇异椭圆方程无穷多解的存在性

吴卓伦，商彦英

西南大学 数学与统计学院，重庆 400715

本文中，我们研究如下问题：

(1)

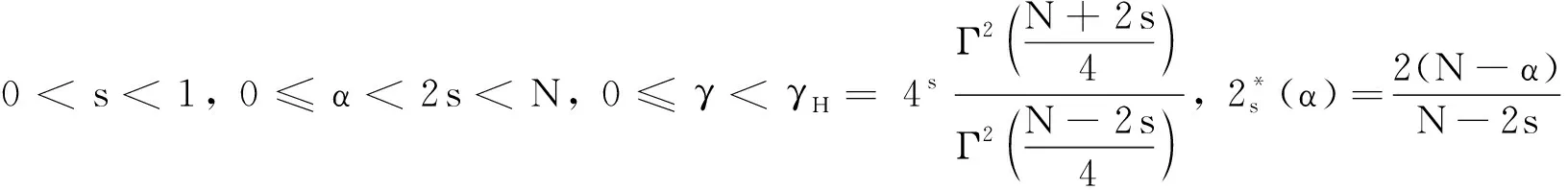
近年来，带有Sobolev-Hardy临界指数的奇异椭圆方程受到广泛关注.当s=1时，方程即是整数阶方程，文献[1-3]利用山路引理得到了这类整数阶方程存在正解，文献[4]利用极大极小值原理得到了其变号解.文献[5-6]在g(x，u)满足关于u是奇函数的条件下，得到了这类整数阶方程无穷多解的存在性.

当0

条件(G)保证了PS序列的有界性.我们在文献[10]的基础上，考虑了分数阶椭圆方程在Sobolev-Hardy临界情况下无穷多解的存在性.在Sobolev-Hardy临界情况下不需要条件(G)也能证明PS序列有界.本文通过文献[11]的方法，在没有条件(G)的情况下，证明了能量泛函在某一范围内满足(PS)c*条件，运用对偶喷泉定理，得到了方程(1)存在无穷多个弱解.

(g3)g(x，-t)=-g(x，t)对所有t∈R和x∈Ω成立.

我们用Hs(Ω)表示分数阶Sobolev空间[12]，其范数定义为

泛函空间为

记空间的范数为

当γ<γh时，Sobolev-Hardy最佳常数[13]定义为

(2)

方程(1)对应的能量泛函为

方程的解与泛函的临界点一一对应.本文中用C，Ci表示各种正常数.

我们的主要结果如下：

引理3假设g满足条件(g1)，则存在常数C>0，使得

(3)

证由条件(g1)可以得到

所以

记

则(3)式成立.

(4)

(5)

(6)

由(5)式和(6)式可知

因为Ω⊂RN是有界区域，所以存在常数C0>0，使得Ω⊂B(0，C0)，且

(7)

由(3)式和(7)式可得

(8)

由条件(g1)可得

因为

所以

故

结合(8)式可得

‖unj‖2≤C6‖unj‖+C7

根据Vitali定理和引理1，有

(9)

由Brezis-Lieb引理和引理1，可以得到

(10)

结合(3)式和(8)式可得

(11)

令

则对任意λ∈(0，λ*)，有

J(u)≥-β0

(12)

(13)

根据(9)式和(10)式可得

根据Λγ，s，α的定义，有

定理1的证明

(B1) 根据条件(g1)，存在常数C8>0，满足

所以

(14)

由Sobolev不等式和Sobolev-Hardy不等式，存在常数R1，R2>0，使得

(15)

则对u∈Yk，‖u‖=rk，有J(u)<0.选取rk<ρk，(B2)成立.

(B3) 根据(15)式，当k≥k0时，u∈Zk且‖u‖≤ρk，满足

J(u)≥-λC8φk‖u‖≥-λC8φkρk