一类传送带问题解的存在性

鲁雄，王跃

1. 贵阳职业技术学院 基础教育部，贵阳 550081；2. 贵州大学 数学与统计学院，贵阳 550025

根据文献[1]的介绍，D’Alembert和Euler首次提出了用来描述弹性弦在横向上微小振动过程中弦的变化模型.后来，文献[2]考虑了由固定端点间弦的长度变化而引起的张力微小变化，形成了著名的Kirchhoff模型

(1)

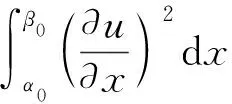
(2)

这里v表示传送带轴向速度，vT>0是常量，f(x，u)≡0.受此影响，令ε=1-v2，我们考虑模型(2)受异号源和反作用控制下的一种推广，即研究问题

(3)

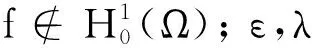
本文的主要结果如下：

证

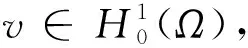
(4)

也就是说泛函I的临界点与问题(3)的解等价.

下面我们分3部完成定理1的证明.

第一步 泛函I满足P.S.条件.

(5)

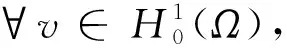
(6)

取v=un，则由(5)式得

注意到0<λ<λ1，

则由

从而有

(7)

由(7)式可知

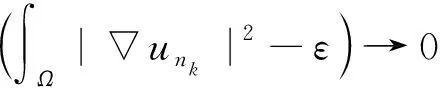
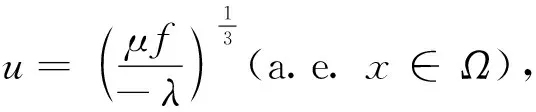
因此

于是

因此{unk}是{un}中强收敛的子列，故满足P.S.条件.

第二步 在定理1的条件下，当ε≥0时，对任意μ>0，可证问题(3)有一个正解.

因此有

由此可知

其中

由f(x)∈L2(Ω)和0<λ<λ1，通过直接计算，得

由此可见，I(u)是强制的且下方有界的连续泛函.

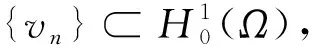
因此，对任意μ>0，由于f∈L2(Ω)且f(x)>0(a.e.x∈Ω)，那么当n→∞时，有

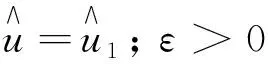
并且I(u*)=0，即u*是I的一个全局极小点.显然u*≠0.从而问题(3)至少有1个非平凡解.

第三步 在定理1的条件下，当ε>0时，存在μ*=μ*(ε，λ)>0，对任意的μ∈(0，μ*)，问题(3)至少存在3个非平凡解.

u+=max{u，0}u-=min{u，0}

那么

u+u-≡0u=(u++u-)

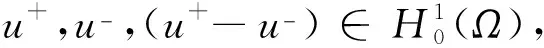
即I(v*)

其次，令

对任意μ∈(0，μ*)，有

也就是说

因此在H-上，类似u*的证明，可得问题(3)存在解u**∈H-.更进一步，根据Pucci三解定理[24]知，泛函I存在异于u*和u**的第三个临界点u***.因此，在定理1的条件下，问题(3)存在3个不同解，这就完成了定理1的证明.

本文根据Ekeland变分原理证明了问题(3)在适当假设条件下解的存在性和多重性.另外，根据文献[22]的介绍，当ε=0时，问题(3)称为临界转速问题，此时的基本固有频率消失，具有发散不稳定性.通常的研究中会假设ε属于次临界的转速范围，即ε>0，这种转速可以理解为发动机在额定功率内的转速.对于燃油或者燃气等材料作为发动机原料的装置，一般来说技术人员的稳定操作总可以使得速度低于临界速度.然而，在电力系统特别是交变电流控制的发动机中，由于电压、电流的不稳定，会导致速度的不稳定，当电流过强时，速度可能会超过临界速度，即ε<0，此时会有烧坏发动机的危险.而当电流过弱时，又可能因为速度过慢而导致发动机线圈发热而烧坏.注意对于燃油或者燃气等材料作为发动机原料的装置，速度过低便会自动熄火而不会烧坏发动机.人们总希望添加适当的同号源或者异号源以及其他形式的装置(非线性项g(x，u)≠0)，来自动控制速度不高于临界速度，同时又不低于可能烧坏发动机的最低速度，以保证发动机正常运行.u3表示异号源，f(x)为反向作用，系数λ，μ可以理解为控制系数.异号源和反向作用主要用来控制发动机过快的速度，以使得转速不超过临界速度.根据问题的需要，并注意到ε=0时的临界速度，因此在物理意义上，问题(3)中的参数ε应该属于区间[0，1]，但从数学研究的角度，将研究范围稍加扩宽也无妨，因此问题(3)的研究是有实际意义的.