n-强投射余可解Gorenstein平坦模

钟魁晨，张翠萍

西北师范大学 数学与统计学院，兰州 730070

文献[1]在左、右Noether环上引入了G-维数为0的有限生成模.文献[2]在任意结合环上引入了Gorenstein投射(内射)模的定义，推广了G-维数为0的有限生成模.文献[3]引入了强Gorenstein投射(内射、平坦)模，并且证明了一个模M是Gorenstein投射模当且仅当它是某个强Gorenstein投射模的直和因子.文献[4]引入了n-强Gorenstein投射(内射、平坦)模，并研究了这类模的一些性质.随着人们对Gorenstein同调理论更为深入细致的研究，文献[5-7]引入了Gorenstein AC投射模、n-强Gorenstein AC投射模，并得出了很好的性质.

文献[8]定义了强Gorenstein平坦模，即Ding投射模.文献[9]研究了PGF模，给出了这类模的一些等价刻画.文献[10]研究了PGF模和Gorenstein平坦模、Ding投射模之间的关系，证明了PGF模的类等于Ding投射模的类和Gorenstein平坦模的类的交集，给出了PGF模的类与Ding投射模的类相等的等价条件.文献[11]研究了强PGF模.文献[12]研究了强Ding投射模，文献[13-14]对这类模进行了深入研究，并证明了这些模类具有许多与n-强Gorenstein投射模类似的性质.

受以上思想的启发，本文引入n-强投射余可解Gorenstein平坦模，研究它的性质，讨论这类模与n-强 Gorenstein平坦模及n-强Ding投射模之间的关系.

本文中的环R均指有单位元的结合环，模指左R-模.设M是R-模，M+表示M的示性模Homz(M，Q/Z)，M⊥表示M的右正交.pdR(M)，idR(M)，fdR(M)分别表示M的投射维数、内射维数、平坦维数.P(R)，GP(R)，DP(R)分别表示投射模类、Gorenstein投射模类、Ding投射模类.

1 预备知识

定义1[9]如果存在投射模的正合序列

定义2[11]如果存在投射模的正合序列

定义3[4]设n是正整数.如果存在R-模的正合序列

其中每个Pi是投射模，且对任意投射模P，HomR(-，P)保持以上序列正合.则称R-模M是n-强Gorenstein投射模，记M为n-SGP模.所有n-SGP模的类记为n-SGP(R).

定义4[13]设n是正整数.如果存在R-模的正合序列

其中每个Pi是投射模，且对任意平坦模F，HomR(-，F)保持以上序列正合.则称R-模M是n-强Ding投射模，记M为n-SDP模.所有n-SDP模的类记为n-SDP(R).

定义5[4]设n是正整数.如果存在R-模的正合序列

其中每个Fi是平坦模，且对任意内射右R-模I，I⊗R-保持以上序列正合.则称R-模M是n-强Gorenstein平坦模，记M为n-SGF模.所有n-SGF模的类记为n-SGF(R).

定义6[4]设n是正整数.如果存在R-模的正合序列

其中每个Ii是内射模，且对任意内射模I，HomR(I，-)保持以上序列正合.则称R-模M是n-强Gorenstein内射模，记M为n-SGI模.所有n-SGI模的类记为n-SGI(R).

我们有

PGF(R)⊆GP(R) PGF(R)⊆DP(R)

P(R)⊆1-SGP(R)⊆n-SGP(R)⊆GP(R)

P(R)⊆1-SDP(R)⊆n-SDP(R)⊆DP(R)

2 主要结果

定义7设n是正整数.如果存在R-模的正合序列

其中每个Pi是投射模，且对任意内射右R-模I，I⊗R-保持以上序列正合.则称R-模M是n-强投射余可解Gorenstein平坦模，记M为n-强PGF模.所有n-强PGF模的类记为n-SPGF(R).

命题1设n为正整数.则：

证设M是强PGF模，则存在R-模的正合序列

其中P是投射模，且对任意内射右R-模I，I⊗R-保持以上序列正合.从而有正合序列

且I⊗R-作用后还是正合的.故M是n-强PGF模.

其中每个Pi是投射的，且对任意内射右R-模I，I⊗R-保持以上序列正合.从而有正合序列

且I⊗R-作用后仍正合.故M是PGF模.

易得以下结论：

命题2设n是正整数，则n-SPGF(R)关于直和封闭.

下面给出n-强PGF模的等价刻画.

定理1设M是R-模，n是正整数.则以下结论等价：

其中每个Pi是投射模，且对任意内射维数有限的R-模H，H⊗R-保持以上序列正合；

其中每个Pi是投射模，且对任意内射右R-模E和某个正整数j，有

其中每个Pi是投射模，且对任意内射维数有限的右R-模H和某个正整数j，有

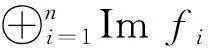
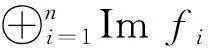
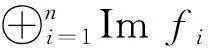
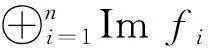
证⟹显然.

其中每个Pi是投射模，且对任意内射右R-模I，I⊗R-保持以上序列正合.

设idR(H)=m<∞.当m=0时，H⊗R-保持以上序列正合.

假设对内射维数等于m-1的右R-模K，K⊗R-保持以上序列正合.考虑正合序列

其中E是内射右R-模，idR(K)=m-1.于是有复形的短正合列

因为E⊗RP和K⊗RP是正合的，所以H⊗RP正合.

所以结论成立.

是R-模的正合列.令Ki=Kerfi(i=0，…，n-1)，Kn=M.对任意内射右R-模，由维数转移可得

其中i为任意正整数.因为

所以

故I⊗R-保持以上序列正合.所以M是n-强PGF模.

其中每个Pi是投射模，且对任意内射右R-模，I⊗R-保持以上序列正合.则对任意1≤i≤n，有正合列

且对这些正合序列作直和，得正合列

其中α=diag{α1，α2，…，αn-1，αn}，f=diag{fn，fn-1，…，f1，f0}.显然

从而有正合列

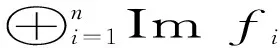
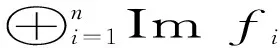
显然，对任意正整数n，强PGF模一定是n-强PGF模，反之不成立.注意到n-强PGF模定义中的每个Imfi也是n-强PGF模.

以下讨论n-强PGF模、n-强Ding投射模及n-强Gorenstein平坦模之间的关系.

引理1n-SPGF(R)⊆n-SDP(R).

证设M是n-强PGF模，则存在R-模的正合列

其中每个Pi是投射的.由命题1知，M是PGF模.由文献[10]的推论1知，M是Ding投射模，所以对任意平坦模故M是n-强Ding投射模.

命题3n-SPGF(R)=n-SDP(R)∩n-SGF(R).

证设M是n-强PGF模.由定义，M是n-SGF模.由引理1知M∈n-SDP(R)∩n-SGF(R).

反之，设M∈n-SDP(R)∩n-SGF(R).因为M∈n-SDP(R)，所以存在R-模的正合序列

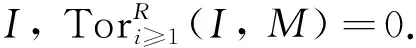
定理2设R是环，以下结论等价：

其中每个Pi是投射模，从而有正合序列

因为图中第一行正合，所以第三行正合.从而有正合列

故M∈n-SGF(R).

其中每个Pi是投射模，从而有正合列

(1)

其中每个Pi+是内射模.设I是内射模，且

P-1=M

从而

则HomR(I，-)保持序列(1) 正合.故M+∈n-SGI(R).