2K1∪In的匹配等价图类

高尚，马海成

青海民族大学 数学与统计学院，西宁 810007

本文仅考虑有限无向的简单图.设G是一个n阶图，G的一个匹配是指G的一个生成子图，它的每一个分支是孤立边或者孤立点，k-匹配是指其中有k条边的匹配.文献[1]定义了图G的匹配多项式为

这里，p(G，k)是G的所有k-匹配的数目，并且约定p(G，0)=1.在文中为了方便，将μ(G，x)简记为μ(G).若图G和H有μ(G，x)=μ(H，x)，则称图G和H是匹配等价的，记为G～H.设G是一个图，以[G]表示图G的匹配等价图的集合，以σ(G)表示集合[G]的元的个数，即|[G]|.若σ(G)=1，称图G是匹配唯一的.

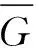
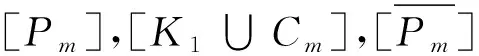
文献[14]的定理1给出了K1∪Pm的匹配等价图类.为了方便，我们将与K1∪Pm的匹配等价的图的集合记为Φ1，则|Φ1|=σ(K1∪Pm).

文献[15]的定理1和定理2给出了2K1∪Pm的匹配等价图类.通过观察我们发现，除了m+1=3×2n-1(n≥3)的情形外，2K1∪Pm的每一个匹配等价图包含且仅包含一个路分支.而当m+1=3×2n-1(n≥3)时，2K1∪Pm的匹配等价图中含有Q(2，1)分支的等价图是：Q(2，1)∪H，H∈Δ4，其中的每一个H有且恰有两个不同的路分支.用Φ2表示2K1∪Pm的每一个匹配等价图中删去一条路分支后得到的图的集合.于是

为了方便，本文用σ(G，H)表示图G的所有匹配等价图中含有分支H的等价图的个数.

引理1若m+1=3×2n-1对某个正整数n成立，则

证H～3K1∪Pm，H1是H的连通分支，使得

M1(H1)=M1(Pm)H=H1∪H2

对n用数学归纳法.当n=1时，结论明显.当n=2时，由文献[16]的引理2，3和4得，H1=P5，C3，T1，1，1，相应地，H2～3K1，3K1∪P2，2K1∪P2，则

σ(3K1∪P5，P2)=0+1+1=2

σ(3K1∪P5，P2∪P3)=0+0+0=0

当n=3时，由文献[16]的引理2，3和4得，H1=P11，C6，T1，1，4，Q(2，1)，T1，2，2，相应地，H2～3K1，3K1∪P5，2K1∪P5，2K1∪P3∪P5，2K1∪P3∪C3，由文献[16]的引理10得

σ(3K1∪P11，P2)=0+2+2+2+0=6

σ(3K1∪P11，P2∪P3)=0+0+0+2+0=2

当n≥4时，由文献[16]的引理2，3和4得，H1=Pm，Cm2+1，T1，1，m2-1(m2+1=3×2n-2)，相应地，H2～3K1，3K1∪Pm2，2K1∪Pm2，由文献[16]的引理10得

设H～3K1∪Pm，H1是H的连通分支，使得

M1(H1)=M1(Pm)H=H1∪H2

(a)m+1=2n+1.当n=1时，σ(3K1∪P3，P2)=0，假设结论对m2+1=2n成立，且对n用数学归纳法，H1=Pm，Cm2+1，T1，1，m2-1，相应地，H2～3K1，3K1∪Pm2，2K1∪Pm2，则

σ(3K1∪Pm，P2)=0+0+0=0

(b)m+1=9×2n-1.当n=1时，σ(3K1∪P8，P2)=0.当n=2时，H1=P17，C9，T1，1，7，T1，2，3，相应地，H2～3K1，3K1∪P8，2K1∪P8，2K1∪C3∪P8，则

σ(3K1∪P17，P2)=0+0+0+0=0

假设结论对m2+1=9×2n-2成立，且对n用数学归纳法，H1=Pm，Cm2+1，T1，1，m2-1，相应地，H2～3K1，3K1∪Pm2，2K1∪Pm2，则

σ(3K1∪Pm，P2)=0+0+0=0

(c)m+1=15×2n-1.当n=1时，σ(3K1∪P14，P2)=0.当n=2时，H1=P29，C15，T1，1，13，T1，2，4，相应地，H2～3K1，3K1∪P14，2K1∪P14，2K1∪C3∪P14，则

σ(3K1∪P29，P2)=0+0+0+0=0

假设结论对m2+1=15×2n-2成立，且对n用数学归纳法，H1=Pm，Cm2+1，T1，1，m2-1，相应地，H2～3K1，3K1∪Pm2，2K1∪Pm2，则

σ(3K1∪Pm，P2)=0+0+0=0

(d)m+1=2n-1(2k+1)，k(≠0，1，4，7)为整数.当n=1时，σ(3K1∪P2k，P2)=0.假设结论对m2+1=2n-2(2k+1)成立，且对n用数学归纳法，H1=Pm，Cm2+1，T1，1，m2-1，相应地，H2～3K1，3K1∪Pm2，2K1∪Pm2，则

σ(3K1∪Pm，P2)=0+0+0=0

引理2若m+1=3×2n-1对某个正整数n成立，则3K1∪Pm的匹配等价图中含有分支P2的图是下面的图：

2K1∪P2∪T1，1，1∪C6∪C12∪…∪C3×2n-2，…，2K1∪P2∪C3∪C6∪C12∪…∪T1，1，3×2n-2-2；

K1∪P2∪T1，1，1∪T1，1，4∪C12∪…∪C3×2n-2，…，K1∪P2∪C3∪C6∪C12∪…∪T1，1，3×2n-3-2∪T1，1，3×2n-2-2；

P2∪T1，1，1∪T1，1，4∪T1，1，10∪…∪C3×2n-2，…，P2∪C3∪C6∪C12∪…∪T1，1，3×2n-4-2∪T1，1，3×2n-3-2∪T1，1，3×2n-2-2；

2K1∪P2∪P3∪Q(2，1)∪C3∪C12∪…∪C3×2n-2；

K1∪P2∪P3∪Q(2，1)∪T1，1，1∪C12∪…∪C3×2n-2，…，K1∪P2∪P3∪Q(2，1)∪C3∪C12∪…∪T1，1，3×2n-2-2；

P2∪P3∪Q(2，1)∪T1，1，1∪T1，1，10∪…∪C3×2n-2，…，P2∪P3∪Q(2，1)∪C3∪C12∪…∪T1，1，3×2n-3-2∪T1，1，3×2n-2-2.

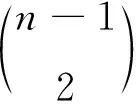
引理3若m≥2是整数，σ(3K1∪Pm，2P2)=0，σ(3K1∪Pm，P2∪P4)=0.

证由引理1和引理2，结果显然.

为了方便，用Φ3表示3K1∪Pm的含有分支P2的所有匹配等价图中删去P2后得到的图的集合，即引理2中的每张图删去P2后得到的图的集合，则|Φ3|=σ(3K1∪Pm，P2).用Φ4表示3K1∪Pm的含有分支P2∪P3的所有匹配等价图中删去P2∪P3后得到的图的集合，即引理2中的每张图删去P2∪P3后得到的图的集合，则|Φ4|=σ(3K1∪Pm，P2∪P3).

为了找到2K1∪Im(m≥6)的匹配等价图类，按m-3所含最大奇因数是1，3，9，15或其他奇数分为5类.

定理1若m-3=2n+1对某个正整数n成立，则

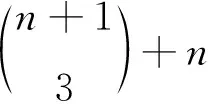
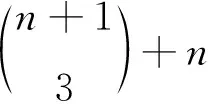
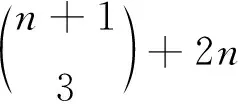
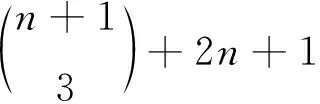
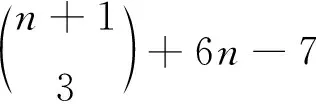
证设H～2K1∪Im，由M1(H)=2及文献[16]的引理2(2)知，H必有一连通分支H1∈Ω2，H=H1∪H2.

(a) 若H1=It(t≥6)，则

2K1∪Im～H=It∪H2

两边并Pm-4，利用文献[16]的引理13(8)得

Pm-4∪2K1∪Im～Pm-4∪It∪H2～Pt-4∪Im∪H2

则

2K1∪Pm-4～Pt-4∪H2

由文献[15]的定理1和定理2知，这样的H2∈Φ2.

(b) 若H1=K1，4，则

2K1∪Im～H=K1，4∪H2

两边并Pm-4∪P2，利用文献[16]的引理13(7)，(8)得

Pm-4∪P2∪2K1∪Im～Pm-4∪P2∪K1，4∪H2～Pm-4∪K1∪I6∪H2～K1∪P2∪Im∪H2

则

K1∪Pm-4～H2

由文献[14]的定理1知，这样的H2∈Φ1.

(c) 若H1=Q(2，2)，Q(3，1)(～Q(2，2))，T2，2，2(～P2∪Q(2，2))，T1，3，3(～P3∪Q(2，2))，T1，2，5(～P4∪Q(2，2))，均可设

2K1∪Im～H=Q(2，2)∪H2

两边并K1∪Pm-4，利用文献[16]的引理13(3)，(8)得

3K1∪Pm-4∪Im～K1∪Pm-4∪Q(2，2)∪H2～Pm-4∪I6∪H2～P2∪Im∪H2

则

3K1∪Pm-4～P2∪H2.

(a) 若H1=It(t≥6)，与的情形(a)类似，这样的H2∈Φ2.

(b) 若H1=K1，4，与的情形(b)类似，这样的H2∈Φ1.

(c) 若H1=Q(2，2)，则

2K1∪Im～H=Q(2，2)∪H2

3K1∪Pm-4～P2∪H2

由引理2知，这样的H2∈Φ3.

(d) 若H1=Q(3，1)，由Q(3，1)～Q(2，2)，与情形(c)类似，这样的H2∈Φ3.

(e) 若H1=T1，3，3，由文献[16]的引理13(5)得

2K1∪Im～H=T1，3，3∪H2～P3∪Q(2，2)∪H2

3K1∪Pm-4～P2∪P3∪H2

由引理1和引理2知：当n≤2时，这样的H2不存在；当n≥3时，这样的H2∈Φ4.

(f) 若H1=T2，2，2.由文献[16]的引理13(4)得

2K1∪Im～H=T2，2，2∪H2～P2∪Q(2，2)∪H2

3K1∪Pm-4～2P2∪H2

由引理3知，这样的H2不存在.

(g) 若H1=T1，2，5，由文献[16]的引理13(6)得

2K1∪Im～H=T1，2，5∪H2～P4∪Q(2，2)∪H2

3K1∪Pm-4～P2∪P4∪H2

由引理3知，这样的H2不存在.

证由文献[16]的引理14，结论显然.