反应堆堆内构件流体激振力的数值模型研究

冯志鹏，黄 旋，刘 帅，沈平川，蔡逢春

中国核动力研究设计院核反应堆系统设计技术重点实验室，四川 成都 610213

引言

反应堆堆内构件（简称堆内构件）是核电站反应堆的主要设备，位于反应堆压力容器内，在高温、高压、强辐照下运行，并且长期承受冷却剂的冲刷[1]。冷却剂的循环流动会引起堆内构件的长期振动[2]，且总是伴随着反应堆的运行而存在，极易导致由流致振动引起的疲劳磨损[3]、噪声[4]等问题，为确保结构在使用寿期内的完整性，只能通过优化结构设计和调整流速，将流致振动引起的结构振动响应控制在可接受的范围之内。因此，堆内构件流致振动理论分析与计算是核电设备安全分析不可缺少的重要内容[5]。

针对核工程中的流致振动问题，国内外学术界和工程界开展了大量的理论、实验和数值分析研究。但由于流致振动问题十分重要但又十分复杂，且堆内构件结构复杂，包含了下部堆内构件、上部堆内构件、压紧弹簧和U 形嵌入件等，同时流致振动经常出现在高雷诺数、非定常、分离流和比较柔性的结构中[6-8]，很难从理论模型上来分析，设计主要依赖于经验系数和实验。Au-Yang 等[9]在反应堆1：9 水力回路上进行了流致振动实验，基于实验数据提出了适用于圆筒结构的随机湍流激励的功率谱密度（PSD）。喻丹萍等[10]针对秦山核电二期工程的堆内构件，做了大量的流致振动实验，其研究结果表明，吊篮流致振动主要是由湍流引起的各态历经的平稳随机振动，吊篮可能出现梁式和壳式振动。梁志坚等[11]应用极值载荷分布法分析了秦山600 MW 核电站堆内构件流致振动实验的实测载荷。张可丰等[12]以堆内构件防断组件为研究对象，研究了随机湍动力、拟静态湍动力、漩涡脱落、吊篮运动等流体激励机理对防断组件流致振动的影响。杨翊仁等[13-14]采用随机振动的模态分析方法研究了吊篮结构缩比模型的流致振动响应。姚伟达等[15]采用实验与计算相结合的分析方法，对秦山核电厂反应堆吊篮的流致振动响应进行了计算。席志德等[16-17]用大涡模拟（LES）方法计算了秦山核电站二期1：5 模型实验的压力容器和吊篮之间环腔内的流场，获取了流体作用在吊篮上的流体压力，Simoneau 等[18]详细介绍了大涡模拟在核能领域用于计算湍流方面的应用，从平均流场、波动的幅值和频率等方面来看，运用大涡模拟与实验结果吻合很好，但需要非常精细的网格，因此，极大地限制了其在实际工程中的应用。

综上所述，流致振动是关系到核反应堆结构设计安全性和可靠性的重要问题，目前要在理论上求解作用于堆内构件表面的脉动压力载荷十分困难，因此，需要采用实验与计算相结合的方法来研究堆内构件的流致振动问题。本文首先建立堆内构件流场区域的几何模型和网格模型，然后建立适用于工程的三维流场分析模型，最后研究各关键部件的流体激振力特性，为堆内构件流致振动分析评价提供关键参数和输入载荷。

1 数值模型

1.1 控制方程

本文中的流体为水，且流速较低，当作不可压缩流体处理。控制方程是N-S 方程，在直角坐标系下表示为[19]

连续性方程

下标：i，j=1,2,3。

1.2 湍流模型

本文主要采用大涡模拟方法[20]对湍流流场进行求解。对N-S 方程在物理空间经滤波即可得到大涡的控制方程

需要使用不同亚格子尺度模型进行建模，本文采用Boussinesq 假设[21]，由涡黏形式计算亚格子湍流应力

下标：k=1,2,3。

此外，在研究流场模型时，还用到了k-ε 及SST两种湍流模型，可参见文献[20]。

1.3 几何模型

堆内构件结构非常复杂，在建立流场分析模型时，须对实际结构进行适当的简化，如忽略局部结构特征、删除连接螺栓、删除螺栓孔、消除过小缝隙、平滑突出结构表面的小构件等，在合理降低计算规模的同时，又充分保留其流场特征。在反应堆压力容器内壁包围的总体空间中，通过布尔运算扣除堆内构件固体区域，即为堆内构件流场分析所需的流体区域，如图1 所示，其中，堆芯段内布置燃料组件，流场十分复杂，由于本文不关注堆芯段的流场细节，因此，通过多孔介质的方式模拟，以减小计算规模。

图1 流体域几何模型Fig.1 Geometry model of fluid domain

1.4 网格模型

流场网格采用ICEM CFD 软件来完成。为了使划分的网格能够尽可能捕捉几何上的精细结构，对关键的面和线创建部件，并对不同部件分别设置网格尺寸。本文将上部堆内构件分为17个部件、下部堆内构件分为46 个部件、堆芯曲面分为3 个部件。对不同的部件分别设置最大尺寸、最小尺寸和网格生长率等参数。参数的设置应保证该部件上的面网格能够较为精确地描述部件的几何边界，特别是对于重点关注区域或对流场影响较大的区域应该设置较小的网格尺寸，以捕捉流场特征。

上部堆内构件、下部堆内构件（不包含堆芯）的流体域结构复杂，采用非结构化网格划分，通过一体化生成方式生成网格，网格细节如图2a、图2b 所示。堆芯部分由于采用多孔介质来模拟，因此，采用六面体网格划分，如图2c 所示。

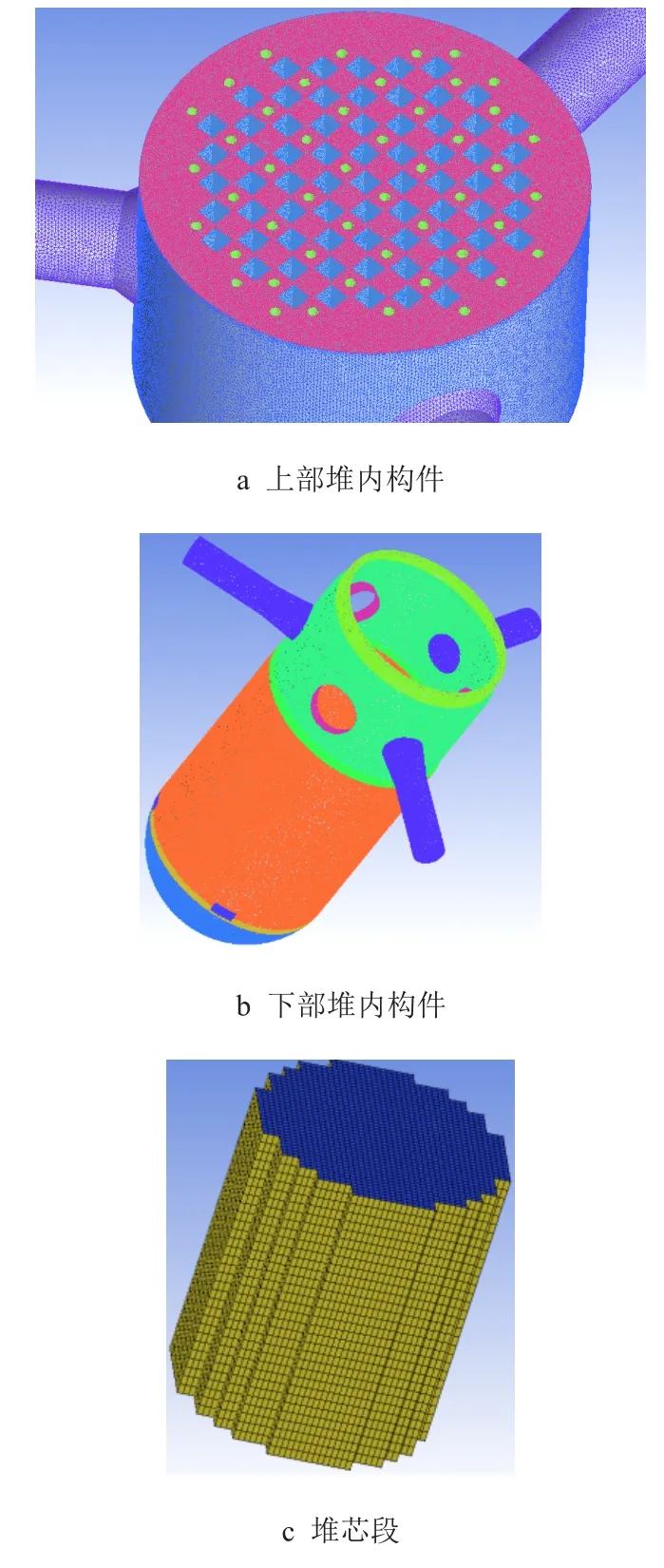
图2 网格模型Fig.2 Grid model

在综合考虑计算资源和计算效率的前提下，进行了一系列网格敏感性测试，以期在计算精度和计算效率之间取得平衡，最终确定了本文流场网格的划分方式和网格尺寸，网格总数为36 050 000。

1.5 计算参数

根据运行压力和进口温度，流体介质的密度为742 kg/m3，动力黏度为9.242×10-5Pa·s。

经过大量计算，本文选取预测结果比较好的3种湍流模型进行对比研究：大涡模拟模型、SST 模型、k-ε 模型。

入口采用速度入口边界条件，其值18.645 m/s。当湍流模型为SST 模型或k-ε 模型时，入口的湍流强度设置为1.5%，水力直径为697.8 mm。3 个出口采用压力出口，设置压强为0。重力方向为z轴负方向，大小为9.81 m/s2。

对堆芯模拟体的压降采用多孔介质模型模拟，由堆芯压降和堆芯模拟题长度可得到多孔介质模型的惯性阻力系数为16.62 m-1。

压力-速度耦合采用SIMPLEC 算法，动量离散为边界中心差分，瞬态求解格式是二阶隐式，采用双精度求解器。时间步长取为0.001 s。

2 三维流场模型分析

2.1 流场特征

以LES 的计算结果为例来分析堆内构件的流场特征。整体反应堆流场的流线分布如图3 所示，可以看出，在上部堆内构件和下部堆内构件的二次支承组件区域流线最为紊乱。

图3 反应堆结构流线图Fig.3 Streamline of reactor

过出、入口管的中心沿反应堆轴向作切面，并在该面上列出速度矢量分布图，分别见图4 和图5，可以看出，整个二次支承区域的流场最为紊乱，并有较大的漩涡产生，而对于上部堆内构件区域，出、入口处的流场较为紊乱，下降段环腔和堆芯部分的流场较为规整，主要是由于堆芯部分采用了简化的多孔介质来模拟，仅关注其压降，而忽略了堆芯的结构细节。从图4 和图5 还可以看出，吊篮与压力容器环腔的流体在两列入口交汇的区域内流体流速较大，作用在吊篮外表面的流体主要沿吊篮的轴向分布，吊篮外表面主要受到轴向流的作用。入口正对的吊篮壁面区域为驻点，压力最大。

图4 出口轴向切面上速度矢量图Fig.4 Velocity vectors in axial section of outlet

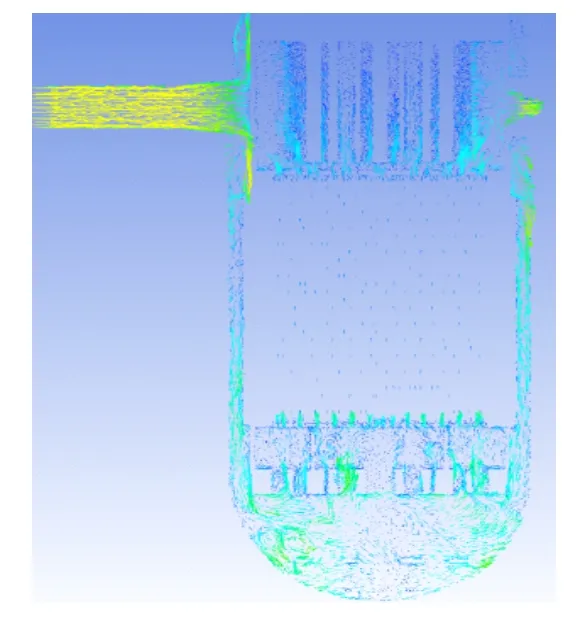
图5 入口轴向切面上速度矢量图Fig.5 Velocity vectors in axial section of inlet

2.2 压力脉动

为了对比研究不同湍流模型对压力脉动的预测能力，取位于吊篮、流量分配板、二次支承柱连接板上的3 个测点的脉动压力进行对比分析，其中，监测点如图6 所示。测点1：吊篮（125°）法兰下，测点2：流量分配板（135°），测点3：二次支承柱连接板（180°）。

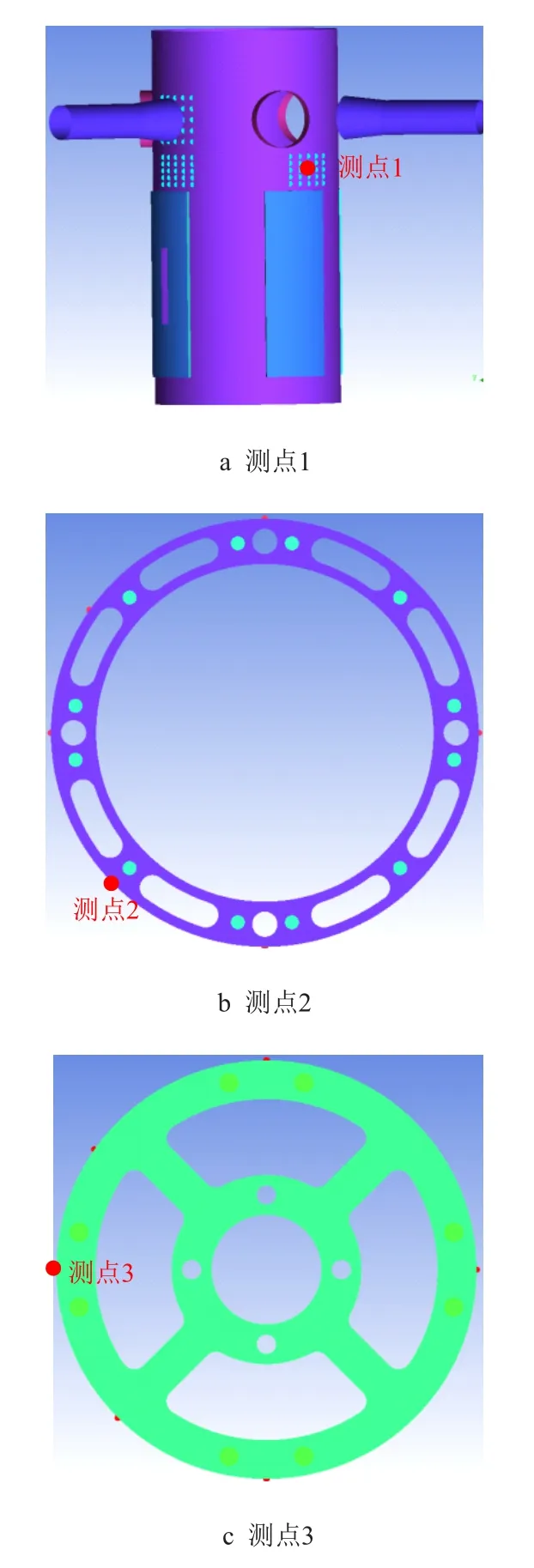
图6 脉动压力的监测点示意图Fig.6 Schematic diagram of monitoring points for pressure fluctuation

图7 给出了利用LES 模型计算出的测点1、测点2、测点3 的压力脉动时程及其功率谱密度曲线（PSD）。从压力脉动的频谱可以看出，各测点处的压力在频域中没有占优的频率，且频率的分布范围较宽，PSD 幅值随频率增加递减较快，这种特点符合宽带随机性，作用在堆内构件上的流体激励力是一种宽带随机过程。

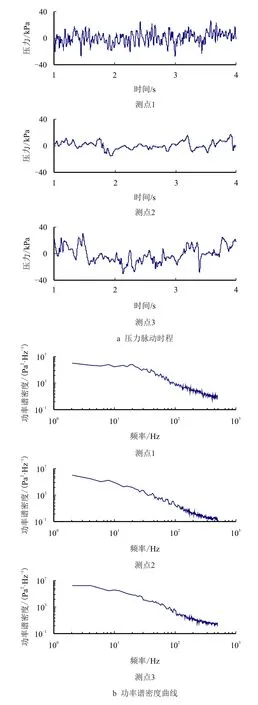
图7 LES 模型预测的各测点的压力脉动时程及PSDFig.7 Time history and PSD of pressure fluctuationfor each monitoring point predicted by LES model

图8 给出了采用SST 模型和k-ε 模型计算出的压力脉动时程及其功率谱密度曲线。可以看出，SST 模型和k-ε 模型计算得到的压力脉动时程比LES 模型计算得到的压力脉动时程平缓，原因在于SST 和k-ε 模型为雷诺时均模型，在计算过程中抹平了湍流的若干细节，而LES 模型可以获得比较精细的流场压力。

图8 SST 模型和k-ε 模型预测的测点1 的压力脉动时程及PSDFig.8 Time history and PSD of pressure fluctuationfor monitoring point 1 predicted by SST model and k-ε model

2.3 3 种湍流模型结果对比

为了更进一步对比这3 种湍流模型对反应堆堆内构件流体激振力的预测情况，将其统计值（均方根值）列于图9 中。

图9 各测点的压力脉动均方根值Fig.9 RMS(Root mean square)value of pressure fluctuation for each monitoring point

从图9 可以看出：（1）在预测吊篮测点的压力脉动时，SST 模型、k-ε 模型的压力脉动均方根值均远小于实验值，严重低估了吊篮上的压力激励水平，而LES 模型预测的结果与实验值吻合较好。（2）在预测流量分配板、二次支承柱连接板的压力脉动时，SST 模型、k-ε 模型、LES 模型的均方根值均比实验结果大，在工程设计时具备保守性。（3）综合对比分析各测点的压力脉动时程、PSD、均方根值，可以得出，LES 模型可以较好地预测反应堆堆内构件的流体激振力，同时又具有一定的保守性，可以用于堆内构件流体激振力的计算。

2.4 流体激振力特性

吊篮是堆内构件中的关键结构，包括吊篮法兰、圆柱形筒体、3 个出口管嘴和堆芯支承板等部件。以吊篮组件为代表结构，分析作用于其上的流体激振力特性。根据反应堆冷却剂的流动特点，流体激振力主要作用于吊篮筒体表面，因此，选择吊篮组件外壁布置监测点。吊篮组件外壁面共布置460 个压力监测点，在z方向分为23 层，每层20 个点，以圆心角18°均分，如图10 所示。

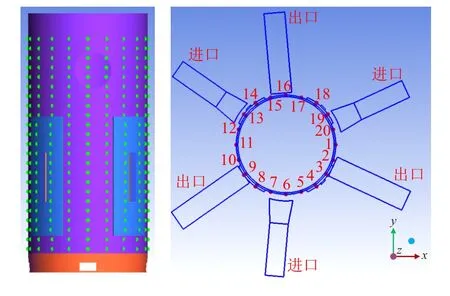
图10 吊篮组件表面上的监测点示意图Fig.10 Schematic diagram of monitoring points on the core barrel surface

图11 给出了吊篮组件表面所有测点脉动压力均方根值的分布情况，从图中可以看到，在进出口位置处（测点标高约-4～-1 m），压力脉动的均方根值变化剧烈且值较大。在远离进出口以下的位置处（测点标高约-8～-4 m），各测点的压力脉动均方根值较小且相差不大。

图11 吊篮组件表面测点的压力脉动均方根值分布情况Fig.11 The distribution of pressure fluctuation RMS value for monitoring points on the core barrel surface

为了进一步详细分析各个标高、各个周向角度处的压力脉动情况，选取位于进口处、出口处、进口与出口之间不同标高的典型测点以及第10 层、第18 层一周的测点进行分析。

图12a 给出了第6 个周向监测点（108°处，位于进口处）的压力脉动均方根值随监测点层数的分布情况，可以看到，压力脉动均方根值从吊篮组件底部到进口处逐渐增大，在靠近进口处下方达到峰值，然后随着监测点层数的增加先减小再增大。图12b 给出了第2 个周向测点（36°处，位于出口处）的压力脉动均方根值随监测点层数的分布情况，可以看到，压力脉动均方根值从吊篮组件底部到出口标高处逐渐增大，在靠近出口标高处下方达到最大值，然后随着标高增加先减小再增大，需要注意的是，由于监测点在层数18 及21 落入吊篮出口位置，所以该处没有监测点。图12c 给出了第5 个周向测点（90°处，位于进口与出口之间）的压力脉动均方根值随监测点层数的分布情况，流场在该部分区域发展的较为充分，受到的扰动也小，所以最具有代表性，可以看出，压力脉动从吊篮组件吊篮底部到进出口标高处逐渐增大，在靠近进出口标高下方处达到最大值，然后随着标高增加先减小再增大。

图12 典型周向测点的压力脉动均方根值随监测点层数的分布情况Fig.12 The distribution of pressure fluctuation RMS value at typical circumferential monitoring points with the layer of monitoring points

图13a 给出第10 层测点（吊篮组件下部）的压力脉动均方根值沿周向角度的分布情况，可以看出，第10 层各测点的压力脉动均方根值是有明显差别的，是由于各点的周向角位置不同，对应出、入口的位置不同导致的，大致为3 个波峰和3 个波谷，3 个波峰对应出口下方附近，3 个波谷对应入口下方附近。图13b给出了第18 层测点（进出口标高处）的压力脉动均方根值沿周向角度的分布情况，其分布规律与第10 层测点的类似，但由于其标高位于进出口标高处，所以各测点间的压力脉动值差异较大。

图13 典型测点的压力脉动均方根值沿周向角度的分布情况Fig.13 The distribution of pressure fluctuation RMS value with the circumferential angle of monitoring points

3 结论

（1）根据堆内构件的流致振动特性建立了堆内构件流场区域的几何模型，在平衡计算资源和计算效率的前提下，确定了流场网格的划分方式和网格尺寸，建立了合理的流场网格模型。

（2）大涡模拟模型可以较好地预测反应堆堆内构件的流体激振力，进而建立了堆内构件流致振动分析的流场模型，获得了三维流场特性。

（3）作用在堆内构件的流体激振力符合宽带随机性，并且计算得到的压力脉动均方根值与相应测点位置的实验值在同一量级，同时又具有一定的保守性，可以用于反应堆堆内构件的流致振动响应分析。