氢冷器回路调节阀开闭过程流场及噪声特性

张 宇，何 超，袁少波

中国核动力研究设计院，四川 成都 610213

引言

调节阀是一种用于调节管道回路压力、流量的典型水力设备[1-2]，广泛应用于核电站常规岛。在常规岛内的氢冷器换热回路中，水流通过氢冷器管束与周围的氢气进行热交换，以保证将氢气温度控制在规定范围内。随着季节或发电功率的变化，通过氢冷器的水流流量是不同的，例如，在夏季时，氢冷器内的换热量较大，此时需要更大的回路流量。因此，调节阀需要人为地或自动地改变其开度，以满足各种流量需求。

在开度调节过程中，由于阀门的过水面积持续变化，导致稳定的流动状态被破坏，势必造成阀门内部的压力波动。由此引发的水力噪声会对环境舒适性以及设备的安全性带来不利影响[3]。因此，有必要较为全面地探究氢冷器回路调节阀在开闭过程中的流场及噪声特性。随着计算机硬件及并行化技术的发展，计算流体力学（Computational Fluid Dynamics，CFD）方法已能较为高效准确地预测复杂流场[4]。崔铭超等[5]为最大限度降低阀芯的振动幅度，通过Fluent 对直角形截止阀的内部流场进行数值计算，进而对截止阀的内部流道形貌进行了优化，最终提高了阀杆的特定方向刚度。徐文涛等[6]使用Fluent 中的宽频噪声模型对大通径气动截止阀的动态流动特性进行了模拟，并依托计算结果对原有设备进行改进，使平均声功率级降低约10%。RYU 等[7]通过CFD 方法获得某节流阀在快速开启过程中的内部非定常流场，并通过Lighthill 声类比方法对内部气动噪声进行了分析。孙卓等[8]借助CFD 方法和LMS Virtual.Lab 声学分析程序对环控系统回路中的蝶形气动阀开展了联合仿真，结果表明蝶形阀开度和来流速度对噪声声压级有较大影响，应避免使蝶形阀长期小开度运行。SEMRAU 等[9]对空化阀内的声共振现象进行了实验和数值研究，他们以测试对象的CFD方法模拟结果对尖锐噪声产生的根本原因进行了探究。徐号钟等[10]结合Fluent 和Actran 软件，采取CFD 和CAA 混合计算方法，对某截止阀及其改进型号进行了数值模拟，总结提取了小孔消声装置的作用机理。

从以上文献中可以看出，应用合适的CFD 和声学方法捕捉阀门（包括截止阀、气动阀和空化阀等）内部流场及噪声特点的做法已较为广泛。而目前对于核能管道中的调节阀研究较少，涉及瞬态工况的更为少见。

本文运用Fluent[11]对氢冷器回路调节阀在关闭开启这一完整过程中的流场展开三维非定常模拟研究，同时借助FW-H 声学类比模型对上述运动过程的水力噪声进行评估，最后，对几种特定开度下的流场及噪声特性进行了分析。

1 数值方法

采取标准k-ε 二方程湍流模型进行数值模拟，对压力-速度耦合方程的求解采用半隐格式（SIMPLE）[12-13]，空间梯度离散格式为基于单元的最小二乘法，压力项采用二阶离散格式，湍流项采用二阶迎风离散格式以提高精度。时间推进步长取0.001 s，每个时间步内迭代计算20 次以保证结果收敛。

1.1 流体控制方程

不可压缩的流场流动特性可通过求解连续性方程和动量守恒方程（N-S 方程）得到。连续性方程（质量守恒定律）的微分形式为[14]

在不可压缩流动中，流体密度不随时间变化，式（1）即可退化成关于微团速度的散度方程。微分形式的N-S 方程为[14]

1.2 标准k-ε 湍流模型

相较于其他雷诺平均湍流模型，标准k-ε 湍流模型已被证明能更好地模拟管道内流流动，且被广泛应用于工业流动计算，其计算开销较为适中[15-17]。该模型的控制方程为

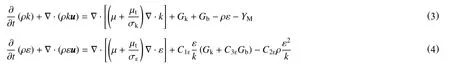
上述参数取值详见文献[18]。

对于管内流动，一般根据基于管道直径的雷诺数Re判断其是否为湍流状态，Re的定义为

式中：Re雷诺数，无因次；

1.3 声学类比模型

采取FW-H 声学类比模型对瞬态流场的时变压力进行处理得到噪声特性，该模型本质上是一种各向异性的波动方程[19-20]。该模型的标量形式为

式（9）右侧第一项表示由湍流引起的四极子声源项，第二项表示由物面脉动压力引起的偶极子声源项，第三项表示由物面加速度引起的单极子声源项。因此，当阀门处于静止时，可忽略单极子声源项，此时只需考虑湍流和脉动压力造成的声源项。而对于开度变化的阀门而言，这3 类声源项均不可忽略。

2 模型及验证

2.1 几何及网格

文中所用调节阀为某核电站常规岛内的真实模型。在获得调节阀各个部件的三维模型后，通过装配、布尔操作及流场域抽取等操作得到100%开度状态下的调节阀流体几何模型。如图1 所示，调节阀模型边界主要包含入口、出口、阀体和阀芯等。其中，阀芯是唯一可动的部件，阀芯的上升或下降会改变阀门内部的过水面积。

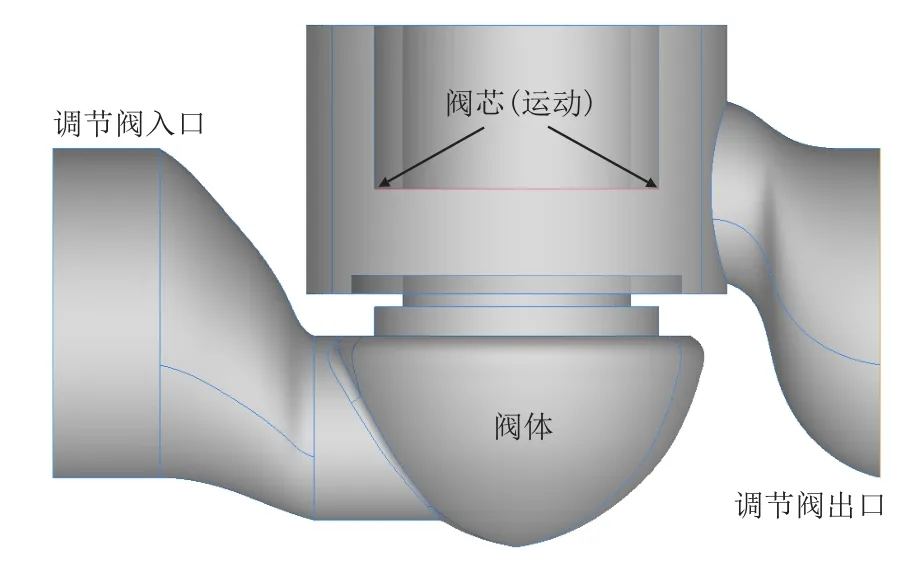
图1 调节阀模型示意图Fig.1 Schema of regulating valve model

该调节阀的出入口直径D=259 mm，阀门沿流向的长度为L=727 mm，阀芯从100%开度到0 开度之间的总行程A=67.8 mm。为保证流体流经调节阀后充分发展，将阀门出口往后延长20L，将阀门入口往前延长8L。

网格划分工具为ICEM CFD，由于调节阀表面造型较为复杂，使用分块结构化网格划分功能难以保证网格质量，故在调节阀内采取全四面体非结构网格剖分，阀门内部的剖面网格如图2 所示。在阀门两侧的管道中采用O-Block 分块方法进行结构网格剖分。两侧管道和调节阀通过Interface 进行数据插值传递，阀门与两侧管道的表面网格见图3。为准确模拟流体的压力沿程损失，布置第一层网格高度为0.5 mm，壁面网格的法向增长率为1.2，图4显示了管道横截面上网格分布情况。

图2 调节阀剖面网格Fig.2 Profile mesh of regulating valve

图3 调节阀与管道的表面网格Fig.3 Surface mesh of regulating valve and pipeline

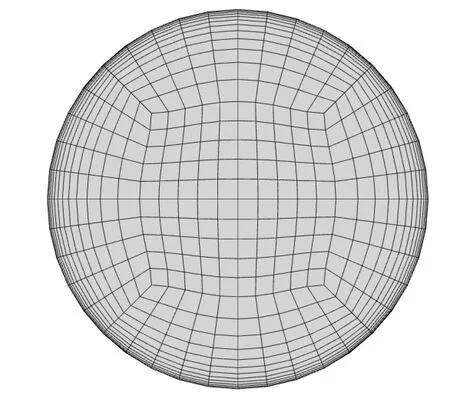
图4 管道横截面网格Fig.4 Cross profile mesh of pipeline

经多次试算及网格无关性验证后，确定最终的模型网格信息见表1。由于管道部分采取的是全六面体网格填充，因此，其网格数量少于调节阀，用于后续计算的网格总数为365 552。其中，管道最低正交质量为0.74，最大网格扭曲率为0.26；调节阀最低正交质量为0.40，最大网格扭曲率为0.55，最大长宽比为882。因此，文中网格可以满足计算要求。

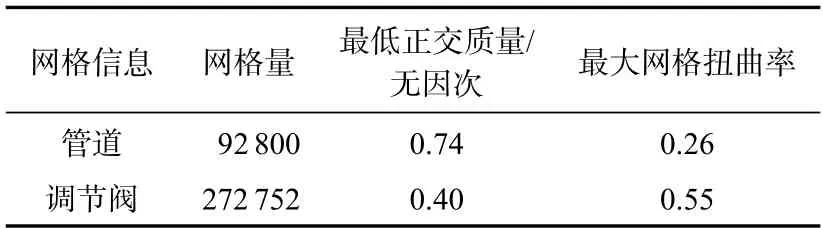
表1 网格信息Tab.1 Mesh information

2.2 动网格

在严格意义上，阀门开度从100% 到0 再到100%被视为一个完整运动周期。但对于使用传统动网格技术的数值模拟，0 开度无法实现。这是因为当阀门开度为0 时，阀芯与阀体会完全接触，此时阀门上下游完全分离，内部流场的拓扑结构发生改变。在阀芯和阀体之间原本存在的网格不会消失而是被无限压缩，此时求解器会因网格畸变而终止计算。可接受的处理方法是，在数值模拟中以一小开度值作为阀门运动的下限。再者，从实际监测值来看，核电厂中的该调节阀开度一般不会低于5%，冬季最低开度基本处于7%～12%，因此，本文规定以10%开度作为阀门的运动下限。

调节阀开度通过阀芯的垂直运动实现，阀芯的位移遵循正余弦变化规律，阀芯从100%开度下降至10%开度这一过程被视为半个周期，到达10%开度后继续恢复至100%开度则完成一个完整周期的运动。周期为4 s，图5 展示了阀芯在一个周期内的位移与速度变化。

图5 阀芯位移与速度时程曲线Fig.5 Time history curves of spool displacement and velocity

网格中的阀芯边界运动由DEFINE_GRID_MOTION 宏实现，该宏主要用于对网格节点进行控制[21]。考虑到文中计算格式为瞬态，需要对该网格节点运动宏进行并行化处理，嵌入到Fluent 中的阀芯边界运动宏见附录。

在部件运动后，流场网格形状将发生变化，若不对网格进行调整，则可能造成网格质量降低甚至产生负体积网格以致计算崩溃。文中调节阀内部的网格通过“网格重构”和“弹簧光顺”方法共同实现位置更新[22]。顾名思义，“网格重构”即重新划分网格，当网格量增多时该方法较为耗时。而“弹簧光顺”的原理是将网格节点用虚拟的弹簧连接，初始状态下各网格节点构成的系统处于平衡状态。当边界上的网格节点发生运动后，将产生一个与连接到该边界节点所有弹簧变形成正比的力，由于系统需要维持平衡状态，这个力就被传播到流场内部的其他网格节点，最后通过计算节点之间的静力平衡方程即可获得更新后的网格节点位置。“弹簧光顺”的数学迭代公式为

弹性常数kij的定义为

式中：

xi，xj网格节点i和j的位置矢量。

特别在与阀芯紧密连接的其他壁面边界上，需使用“网格重构”方法进行面网格更新，否则，在阀芯运动过程中会出现局部面网格质量迅速降低的现象，严重影响计算精度。

3 方法验证

选取10%、30%、50%、70%和100%开度下的调节阀模型作为验证对象。由文中方法计算得到上述各开度下的调节阀相对流量，并与阀门流量特征曲线进行对比，以验证数值计算方法的可靠性。图6展示了数值计算与出厂流量特性曲线的关系，可见数值计算结果与出厂结果的差距很小，表明本文数值方法可被用于后续计算。

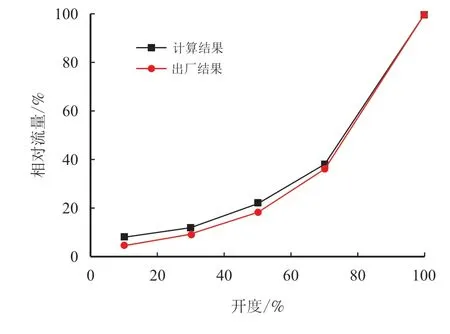
图6 流量特性对比Fig.6 Comparison of flow flux feature

4 结果和讨论

取常温（20°C）下的水作为流体介质，其密度ρ=998 kg/m3，黏度μ=0.001 Pa·s，参考压力为101 325 Pa。取来流雷诺数Re=8.3×105，由式（5）可知，管道入口对应的内流流速V=3.2 m/s，管道入口的湍流边界条件由湍流强度和水力直径确定，由式（8）可知，入口湍流强度为3%，水力直径等效为调节阀出入口直径D。表2 统计了管道出入口的边界类型及初始条件。

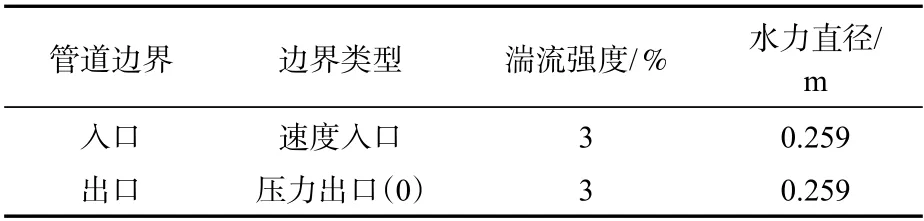
表2 边界初始条件Tab.2 Boundary initial conditions

噪声监测点的设置见图7，监测点1、2 分别位于阀芯与下游管道衔接处的左、右侧，这两处监测点靠近阀芯运动轨迹，因此，其压力及速度场会产生明显的瞬态变化，能较为清晰地体现噪声特性。

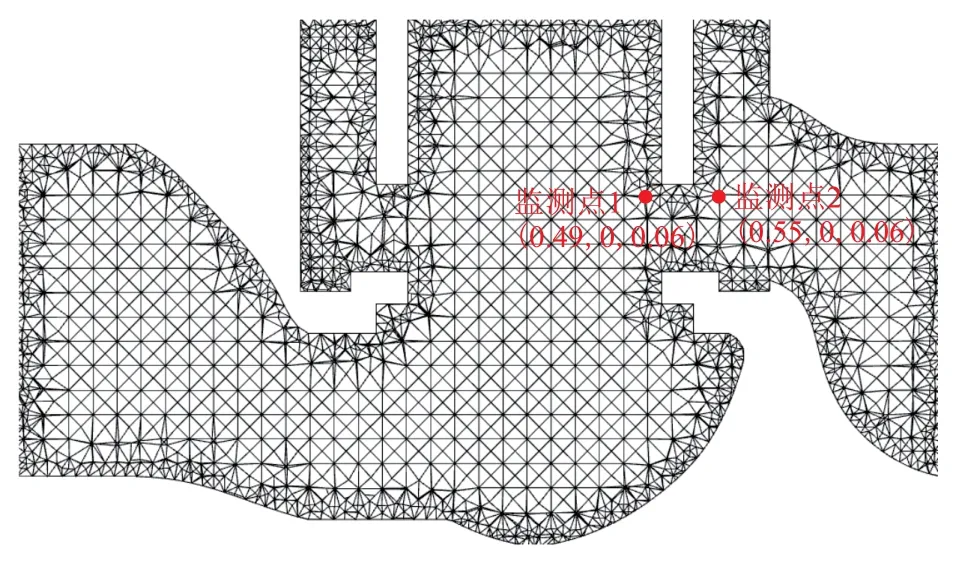
图7 水力噪声监测点Fig.7 Hydraulic noise monitoring points

4.1 调节阀瞬态流场

图8 展示了在0.1，1.0，2.0，3.0 和4.0 s 时调节阀计算域剖面上的静压分布。可以看到，在调节阀与管道的衔接处没有出现明显的压力间断，说明Interface 起到了很好的数据插值传递效果。随着阀芯的下降，调节阀内的压力逐渐增大，当阀芯下至最低处（对应10%开度）时，调节阀内大部分区域达到压力峰值。从图8 可见，在10%开度下（2.0 s），阀芯外围区域的压力还未达到峰值，存在一定的延时现象。

另外，图8 中1.0 s 和3.0 s 对应调节阀开度均为50%，只不过1.0 s 的状态处于关闭过程，而3.0 s处于开启过程。从图中可见，在50%开度下的压力分布基本一致，在3.0 s 时阀芯出口部位的局部压力略有增高。总体而言，在阀芯的关闭开启过程中，调节阀内部压力分布的对称性较好。

图8 不同时刻剖面压力分布Fig.8 Profile pressure distribution at different time

图9 展示了在0.1，1.0，2.0，3.0 和4.0 s 时调节阀计算域剖面上的速度分布。从时间历程来看，体现的速度场周期性较差，1.0 s 和3.0 s 对应的流体速度分布较为不同，在调节阀与下游阀门连接处显得尤为明显。1.0 s 时调节阀下游的大流速流体主要集中在管道上部，而3.0 s 时的大流速流体出现在管道下部。从图9 还可以看到，最大速度主要分布在调节阀内部的拐角处，此处出现较强的流动分离，会导致该处形成局部低压区，进而引起该处流速增大。当开度最低时，阀芯通道内的流速迅速增大，符合基本认识。

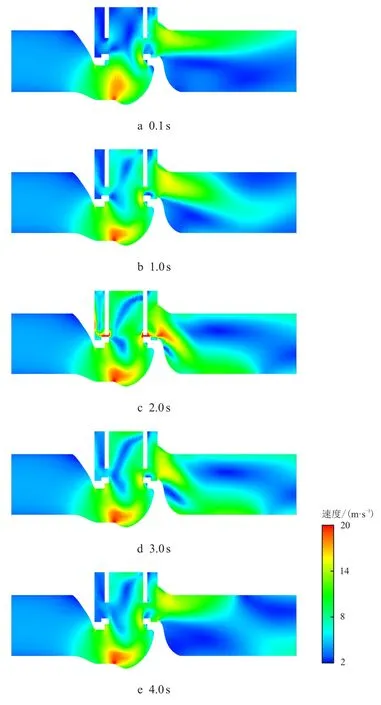
图9 不同时刻剖面速度分布Fig.9 Profile velocity distribution at different time

图10 显示了监测点1、2 处的静压时程变化，可以看到，监测点1 在整个阀芯运动过程中的压力具有良好的对称性，其最大静压约为1.5 MPa，在2.0 s 时取得，这与图8 中的压力分布云图一致。而监测点2 在整个计算周期内的压力分布较为混乱，不具备对称性，不过在开度较小的状态下其压力值仍较高。监测点2 处的压力波动体现出调节阀与下游管道连接处的流动状态受开度影响较大。

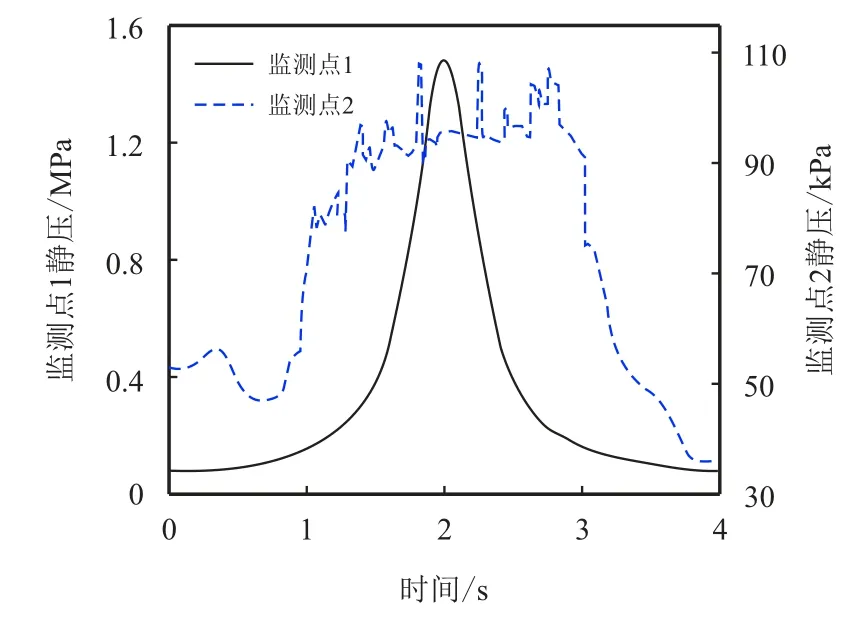
图10 监测点的静压时程曲线Fig.10 Time history curves of pressure at monitoring points

4.2 瞬态噪声特性

在得到阀门移动和静止壁面的瞬态压力脉动值后，通过傅里叶变换即可得到四极子、偶极子和单极子噪声源。图11 给出了监测点1、2 的声压级频率响应曲线。从该频率响应曲线可知，由阀芯运动造成的水力噪声没有明显的主频，可以理解成一种宽频噪声，且声压级随频率的增加而缓慢降低。

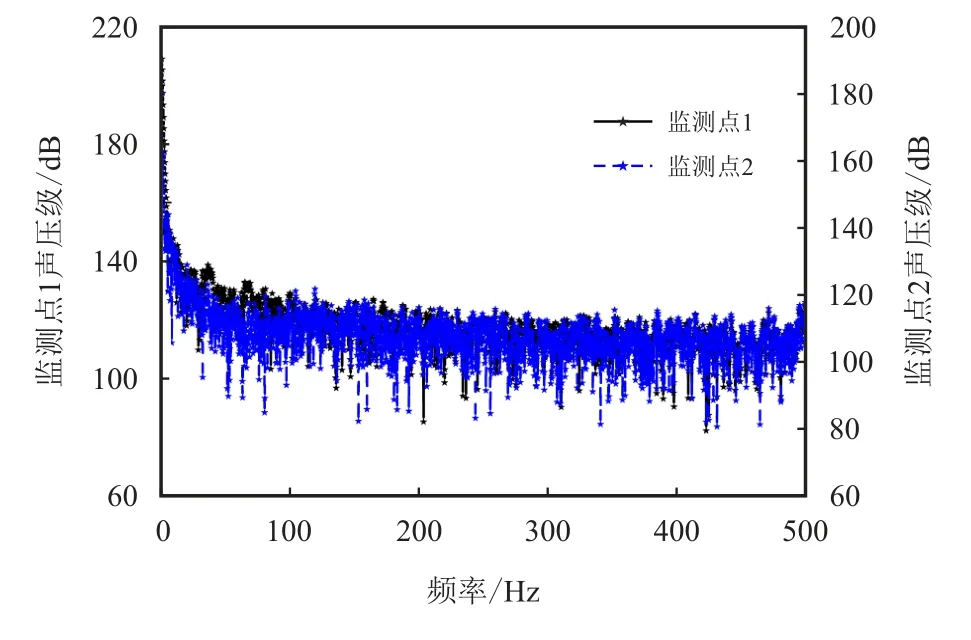
图11 监测点的声压级频率响应曲线Fig.11 Frequency response curves of sound pressure level at monitoring points

监测点1 以50 Hz 为中心的声压级为118.3 dB，以200 Hz 为中心的声压级为114.6 dB，以300 Hz 为中心的声压级为113.1 dB。监测点2 以50 Hz 为中心的声压级为105.3 dB，以200 Hz 为中心的声压级为109.7 dB，以300 Hz 为中心的声压级为102.7 d-B。总体而言，监测点2 处的声压级比监测点1 低约8%。

4.3 典型开度下的噪声特性

本节对调节阀在100%、50%和10%3 种开度下开展了流动噪声特性对比，如图12～图14 所示。

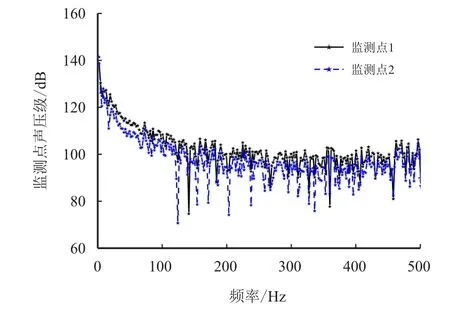
图12 100%开度下的声压级频率响应曲线Fig.12 Frequency response curves of sound pressure level at 100%opening

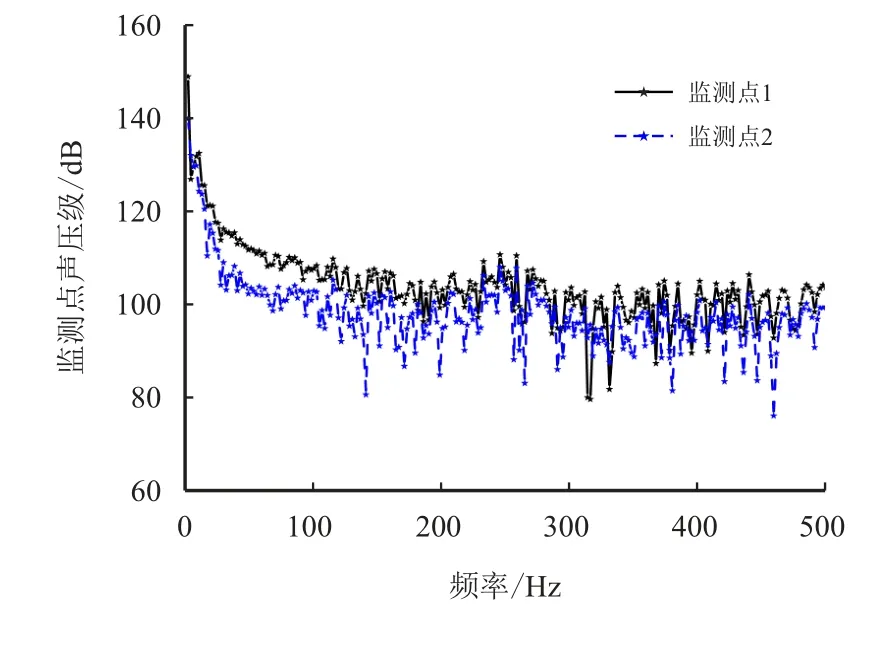
图13 50%开度下的声压级频率响应曲线Fig.13 Frequency response curves of sound pressure level at 50%opening

图14 10%开度下的声压级频率响应曲线Fig.14 Frequency response curves of sound pressure level at 10%opening

在这3 种典型开度下，水力噪声类型均为宽频噪声，且监测点2 处的声压级均小于监测点1。随着调节阀开度的降低，监测点1、2 处的声压级逐渐升高，这是由于开度降低后，流体通过阀芯的过水面积减小，促使流体流经阀芯后产生更剧烈的回流、局部涡流等情况。另外可见，在100%开度下，监测点1、2 处的声压级有较大的重叠区域，随着调节阀开度的降低，重叠区域逐渐缩小，即两处监测点的声压级差距逐渐增加。

5 结论

（1）k-ε 湍流模型对于带阀门的管道内流具有良好的预测精度。

（4）当调节阀处于小开度状态时，阀门整体噪声较高，且阀门内外的噪声水平差距较大。

附录

嵌入到Fluent 中的阀芯边界运动宏