窄安全密度窗口重力置换漏喷函数研究

王存新，许佳欣，李 勇，李 皋，肖 东

1.中国石化西南石油工程有限公司钻井工程研究院，四川 德阳 618000

2.油气藏地质及开发工程国家重点实验室·西南石油大学，四川 成都 610500

引言

在钻井过程中，当钻至裂缝性地层时，由于碳酸盐岩对井筒压力相对敏感等原因，往往会遇见重力置换现象，导致溢流、井漏等复杂情况的出现[1-2]。重力置换是指在近平衡的条件下，钻至裂缝性地层时，由于密度差异，地层中的气体与井筒中的液体发生置换，引起溢流与井漏同时发生的一种现象。关于重力置换发生的条件，目前还没有统一的认识。根据已有的研究成果[3]，发生重力置换需要满足以下4 个条件：（1）存在裂缝；（2）裂缝高度适当；（3）地层空间充足；（4）井筒压力与地层压力在重力置换窗口内。如果不能及时应对，重力置换有可能引起更加严重的井下事故[4-5]。针对这些问题，目前已有许多学者进行过研究。舒刚等[3]研究了在重力置换发生时溢流和井漏的机理，建立了一种漏喷同存的数学模型，并研制了一套模拟重力置换的实验装置，通过实验验证了数学模型的结果，提出了裂缝中存在气液分界面是重力置换发生的重要特征这一观点。张兴全等[6-7]分析了井底压力、井口回压及井底含气量等因素对重力置换的影响。杨顺辉[8]设计了一种可视化的重力置换室内模拟装置。Ozdemirtas 等[9]、林雍森[10]研究了地层的呼吸效应对重力置换现象的影响。孔祥伟等[11]提出了一种区别重力置换导致的气侵和溢流导致的气侵的理论方法。戴成等[12]根据k-ε 双方程模型对气液重力置换流动展开了仿真计算，计算结果表明，三维裂缝流道中都是钻井液下部侵入，呈现一个近似的直角三角形形状，与实验结果相同。赵向阳等[13]研究了稠油与钻井液的重力置换规律，并提出了控制方法。路保平等[14]研究了伊朗雅达油田的重力置换的规律。Petersen 等[15]提出了一种适用于复杂井控条件下的漏喷同存模拟器。郑述全等[16]提出了一种高含硫气井漏喷同存时适用的应对方法。刘绘新等[17]研制了裂缝性气藏重力置换溢流规律实验装置并获得实用新型专利，通过实验分析了重力置换溢流的发生机理和气流后井筒内的气体滑脱特征，提出了相应的井控措施。Xiao 等[18-19]建立并求解了气液重力置换和液液重力置换的数学模型，并通过实验验证了数学模型的准确性，分析了不同裂缝宽度，不同沥青黏度、不同钻井液密度和黏度对液液重力置换的影响，提出堵塞裂缝是控制重力置换的最有效手段。Jeong 等[20]通过统计法生成裂缝面，基于有限元模拟指出沟槽流的最优路径随应力大小而变化。Baghbanan 等[21]、Ivars[22]采用离散元方法研究了裂缝岩体的等效渗透系数张量，模拟了岩体开挖水流从裂隙渗入的过程。Iwai[23]讨论了单裂缝岩体渗透率与外加渗流体的压力梯度，建立了两者的函数关系。

综上所述，对于高压含气层钻井重力置换及气侵规律，已有许多学者进行过研究，但仍然存在如地层裂缝取值固定、研究参数较少等局限。本文在前人研究的基础上，建立了一套高压含气层钻井重力置换数学模型，形成窄安全密度窗口重力置换漏喷函数，同时设计了一套高压含气层地层-井筒重力置换可视化实验装置，并通过实验进行验证。

1 高压含气层钻井重力置换数学模型建立

根据文献[3]，在垂直井筒的情况下，建立模型时需要作如下假设：

（1）垂直裂缝被井筒全部贯穿；

（2）裂缝为高度恒定、宽度相等的平板裂缝；

（3）裂缝面为非渗透性壁面；

（4）气体和液体在裂缝中流动时均视为不可压缩流体；

（5）流动过程为稳态流动。

按照假设建立的重力置换模型如图1 所示。

图1 重力置换物理模型Fig.1 Physical model of gravity displacement

根据图1 模型，建立三维直角坐标系，其中，x轴为裂缝延伸方向（即水平方向），y 轴为重力方向（即垂直方向），z轴垂直于裂缝面。则气体连续性方程为

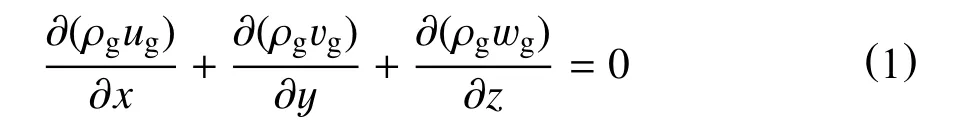
气体动量方程为

液体连续性方程为

液体动量方程为

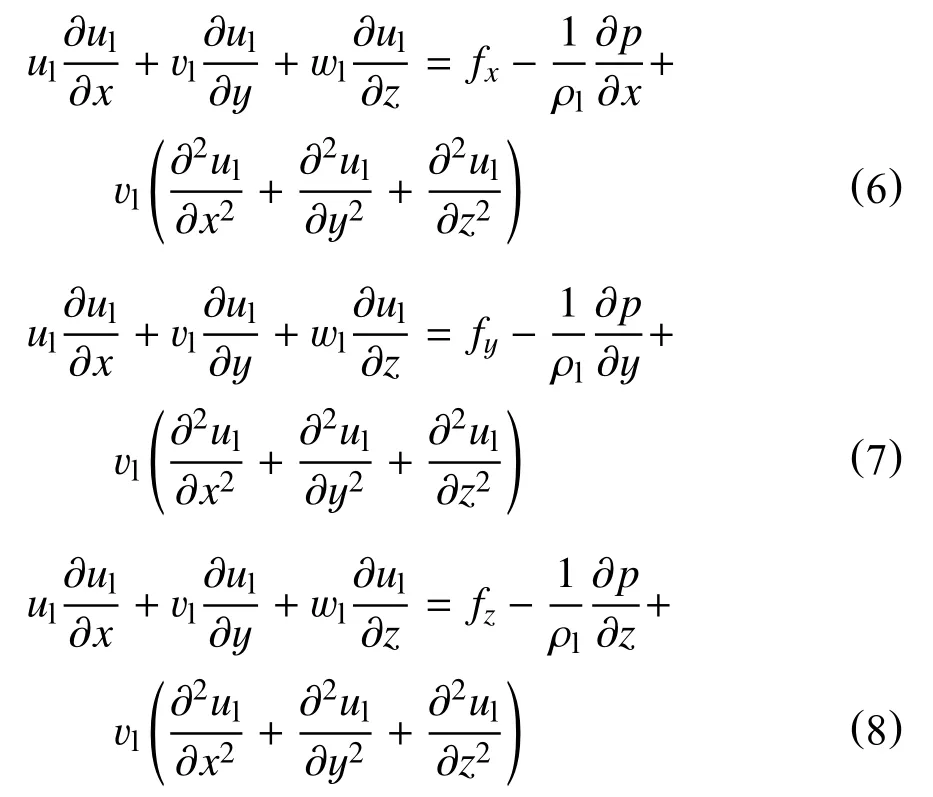
本文采用VOF 模型对气液界面进行研究，通过对气液界面的连续性方程、动量方程及VOF 界面追踪法的运用来确定气液分界面的位置。VOF 法界面追踪方程及表面张力的散度方程

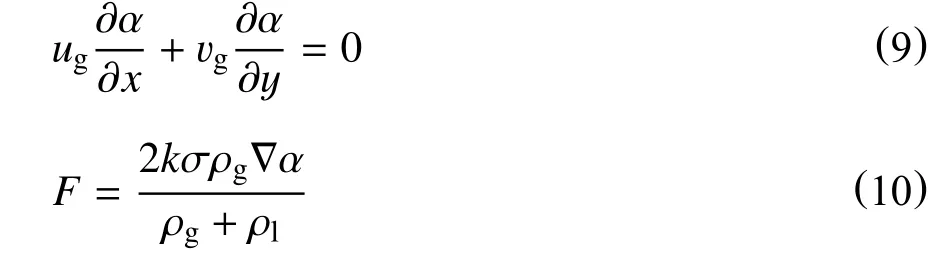
α=1 时，表示在该单元中充满液体；α=0 时，表示该单元充满气体；α ∈（0,1）时，表示该单元含有气液相界面。通过式（10）来求解α 的值就可以得到气液界面的位置。

由于在求解气液界面时，难以分辨出在z方向上气液界面的变化，所以，不考虑气体、液体在z方向上流速的变化，将流动简化为二维模型，即在裂缝宽度方向上速度为定值。同时，为满足工程计算的要求，作进一步假设：

（1）气液重力置换流动已经达到了稳态流动的状态；

（2）液体在裂缝内的流动为二维层流流动（即wl=0）；

（3）气体在裂缝内的流动为一维流动（即wg=0,vg=0）。

经过以上假设后，裂缝内气液重力置换流动的简化模型由气体连续性方程、气体动量方程、液体连续性方程、液体渗流方程及辅助方程共同构成。

气体连续性方程

气体运动方程

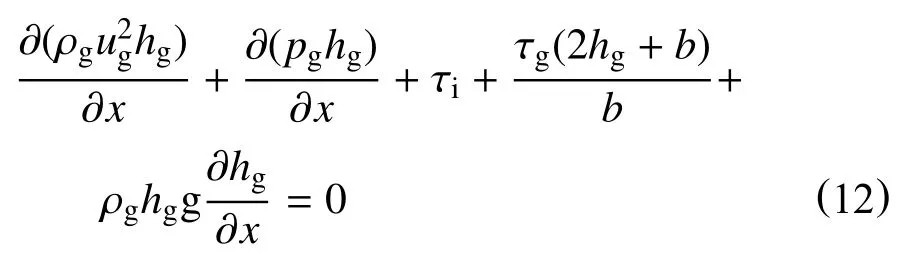
液体连续性方程

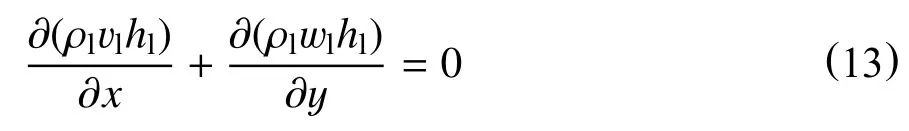
辅助方程

边界条件

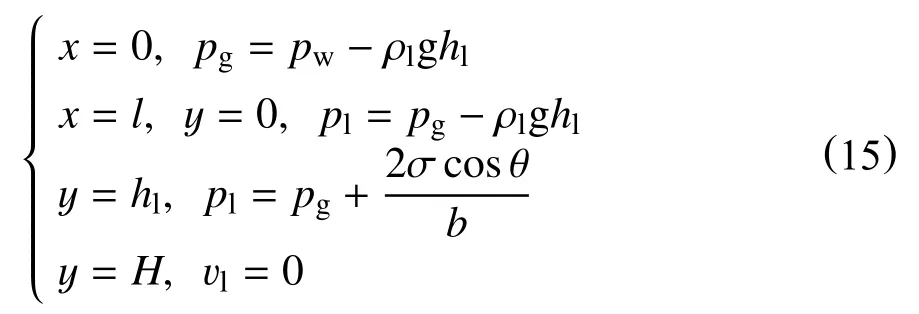
本文采用二维渗流自由界面的方法来计算气液重力置换流动。根据式（15）的边界条件，对上述气液置换流动数学模型进行编程迭代求解，从而得到钻井液的漏失流量、气体溢流量及裂缝内压力分布等数据。求解流程如图2 所示。

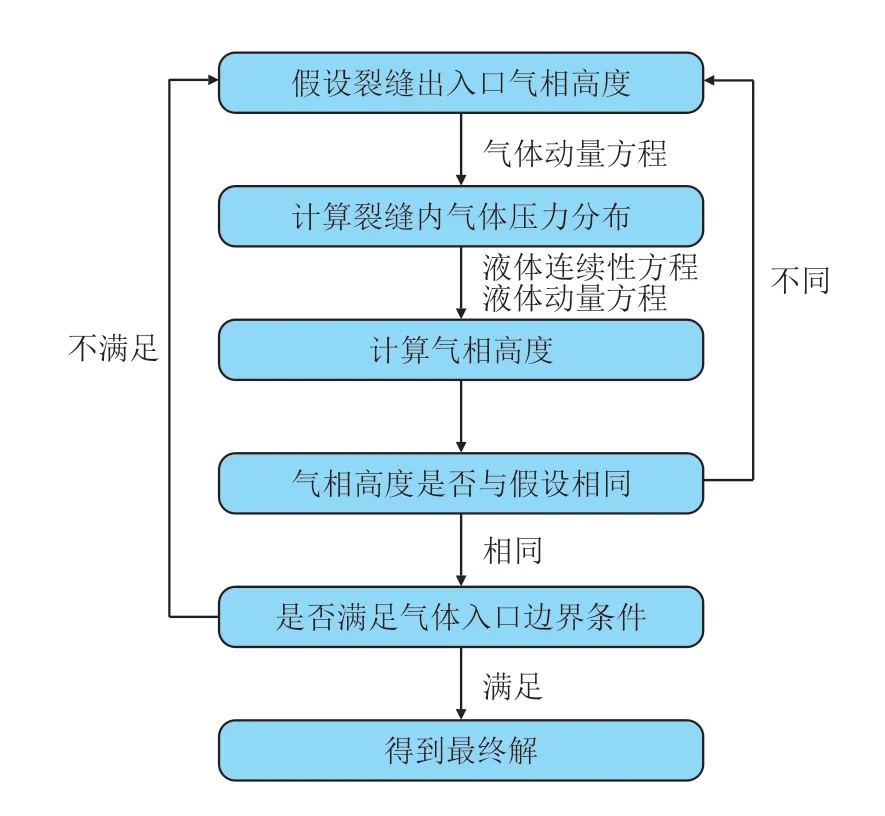
图2 气液置换流动数学模型计算流程Fig.2 Calculation process of the mathematical model of gas-liquid displacement flow

2 重力置换漏喷函数

根据图2 所示求解流程，求解式（11）～式（15），得到缝洞性地层气体溢流流量及钻井液漏失流量与井底压差的关系如图3 和图4 所示。

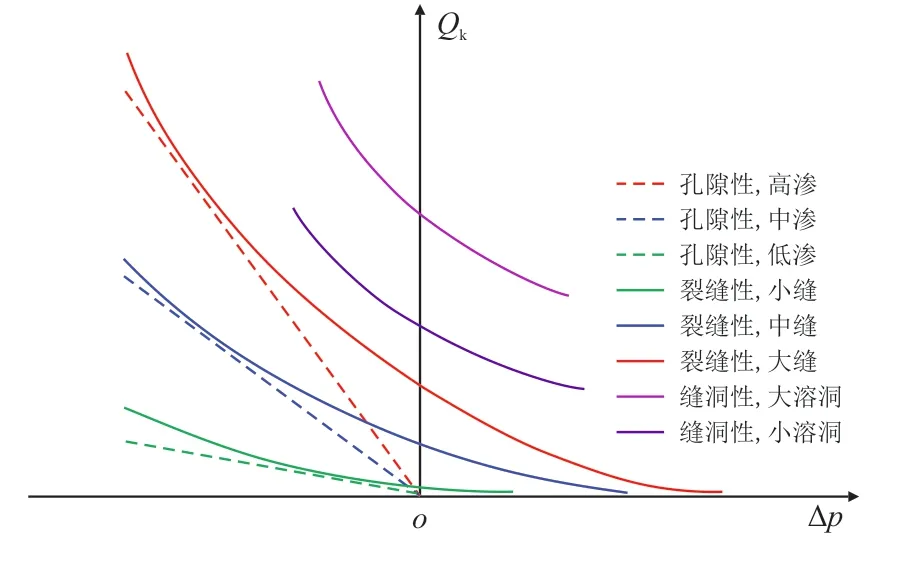
图3 缝洞性地层气体溢流流量与井底压差的关系Fig.3 Relationship between gas overflow rate in fractured-vuggy formations and bottom hole pressure difference

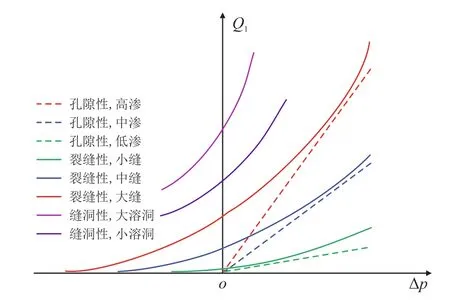
图4 缝洞性地层钻井液漏失流量与井底压差的关系Fig.4 Relationship between drilling fluid loss rate bottom hole pressure difference in fractured-vuggy formations

由图3 和图4 可以看出：（1）对于孔隙性地层，仅在井底负压差时发生溢流，气体溢流流量与负压差成正比，与孔隙度成正比；孔隙性地层仅在井底正压差时发生井漏，钻井液漏失流量与正压差成正比，与孔隙度成正比；（2）对于裂缝性地层，重力置换现象较为明显，当井底趋向于负压差时，气体溢流流量增大，钻井液漏失流量降低并趋近于零，反之趋向于正压差时，气体溢流流量降低并趋近于零，钻井液漏失流量增大；同等井底压差下，裂缝越宽，其钻井液漏失流量及气体溢流流量越高；（3）对于存在溶洞的地层，其重力置换规律与裂缝性地层基本一致，但在井底压差一定的情况下，其钻井液漏失流量和气体溢流流量要大得多。

假设发生井漏时，钻井液漏失流量Qk为负值，则可将图3 与图4 进行整合，得到图5。

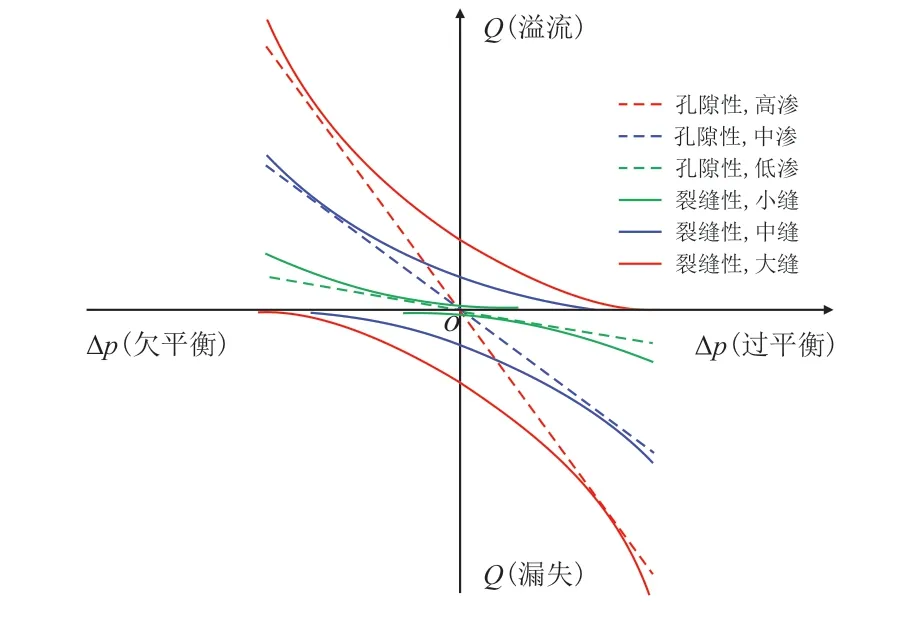
图5 缝洞性地层钻井液漏失流量和气体溢流流量与井底压差的关系Fig.5 Relationship between drilling fluid loss rate and gas overflow rate of fractured-vuggy formations and bottom hole pressure difference

结合本文建立的数学模型，采用斜勾函数建立描述缝洞性储层重力置换规律的数学模型，高压含气层窄安全密度窗口重力置换问题漏喷函数。

气体溢流量与井底压差的关系

钻井液漏失流量与井底压差的关系

实际地层的重力置换规律的描述，可以以上述框架模型为基础，通过现场监测的实际漏喷数据确定式（16）与式（17）中的待定系数。再利用式（16）与式（17），即可获得施工现场的气体溢流流量、钻井液漏失流量与井底压差的关系。图6 为系数a1=0.5，a2=2.0，b1=1.0，b2=1.0 时，不同井底压差下的气体溢流流量及钻井液漏失流量的变化趋势，亦为此区块的漏喷函数图版。

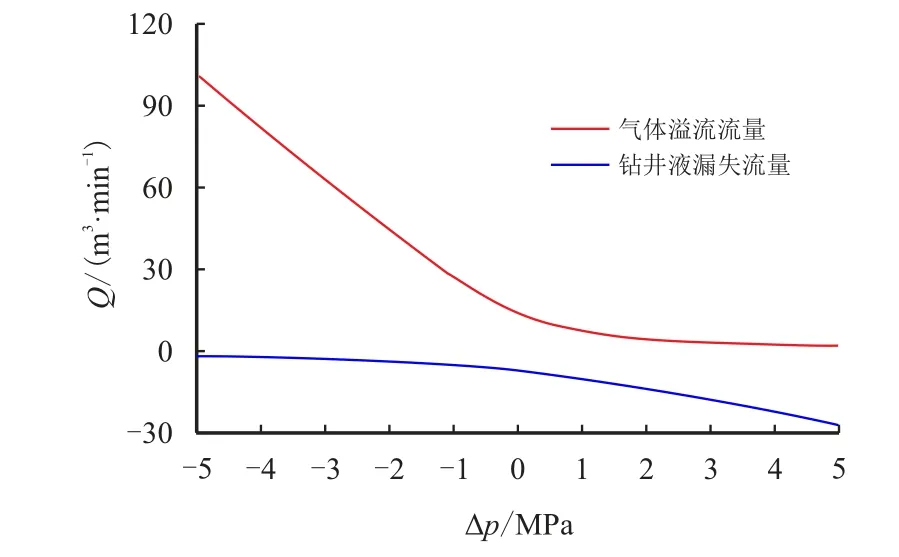
图6 不同井底压差下的气体溢流流量及钻井液漏失流量Fig.6 Gas overflow rate and drilling fluid loss rate under different bottom hole pressure differences

由图6 可知，当井底压力处于欠平衡状态时，井筒中的气体溢流流量随负压差增大量逐渐增大，钻井液漏失流量则逐渐减小直至趋近于0；当井底压力处于过平衡状态时，井筒中的钻井液漏失流量随正压差增大而增大，气体溢流流量则逐渐减小直至趋近于0；当压差处于±5 MPa 时，则会发生重力置换，出现漏喷同存的情况。

因此，只要通过现场的实际漏喷数据确定待定系数a1、a2、b1及b2，即可通过本文所述方法获取针对该区块的漏喷函数图版，为下一步施工决策提供依据。

3 重力置换漏喷函数验证实验

重力置换数学模型能够较好地描述重力置换现象。但是在实际现场施工中，裂缝的数据是未知的，仅凭数学模型不能得到有实际意义的定量化结果，因此，需要结合室内实验，提出可以用于现场施工的漏喷函数。

3.1 实验目的与实验装置

为了验证本文所建立的漏喷函数，利用西南石油大学地层-井筒耦合流动可视化实验装置[24]开展了近平衡状态下的漏喷临界点实验研究。

整个装置主要由井筒-裂缝-地层系统、循环系统及数据采集系统3 个部分组成。井筒-裂缝-地层系统包含井筒模块、裂缝模块及地层模块。为真实反映控压降密度钻井过程中井筒的压力状态，可通过控制井筒与地层模块的回压阀调节井筒与地层的压力关系，模拟井底欠平衡、近平衡及过平衡3种状态。实验装置的效果图及实物图如图7 所示。

图7 地层-井筒耦合流动可视化实验装置效果与实物图Fig.7 Effect and physical map of the visualization experimental device for formation-wellbore coupling flow

3.2 实验过程与实验现象

3.2.1 实验步骤

（1）调节模拟钻井液密度至1.03 g/cm3、表观黏度至30 mPa·s，调整裂缝宽度至1.3 mm，利用空气模拟地层产气；

（2）开启螺杆泵，使钻井液充满井筒并循环一段时间，达到井筒流体流动稳定；

（3）开启空压机，准备实验所需压缩空气；

（4）漏失临界点（上临界）实验：缓慢调节地层模块回压阀，观察到有地层气体进入井筒后，再进行微调，直至液体刚好封住裂缝与井筒连通的通道，待稳定后，记录实验数据；

（5）溢流临界点（下临界）实验：继续缓慢调节地层回压阀，当观察到液体靠近裂缝右下边界时，再进行微调，直至液体流至裂缝与地层连通的通道边缘，待稳定后，记录实验数据。

3.2.2 实验现象

漏失临界点（上临界）实验的典型现象如图8 所示，左侧气液分界面刚好与裂缝左侧上缘平齐，此时为气体不进入井筒的极限压差，即为置换现象的上临界压差。

图8 上临界点实验现象Fig.8 Experimental phenomenon of the upper critical point

溢流临界点（下临界）实验的典型现象如图9 所示，右侧气液分界面刚好与裂缝右侧下缘平齐，此时为钻井液不漏入地层的极限压差，即为置换现象的下临界压差。

图9 下临界点实验现象Fig.9 Experimental phenomenon of the lower critical point

3.3 实验数据及分析

由于发生置换现象的气流量测试困难，而钻井液量测试相对方便，因此，以置换的模拟钻井液流量作为验证依据，实验数据如表1 所示。

根据实验的实际漏喷数据，可确定式（17）中的待定系数a2=1.818 71，b2=1.2×10-6，将理论模型计算的钻井液置换量与实验数据对比如图10 所示。

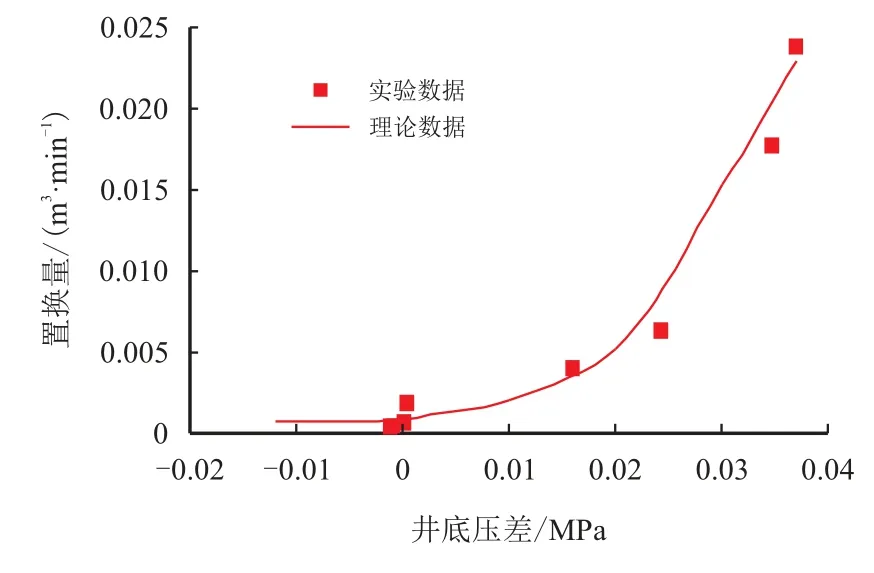
图10 实验测试与模型计算对比图Fig.10 Comparison of experimental test and model calculation

从图8 和图9 的实验现象及表1 的实验数据可以看出，对于裂缝性地层，当井筒与地层压差处于某个区间时，会发生溢流、漏失共存的重力置换现象，即使井底压差为0，也有井底流体的双向流动。

结合图8、图9 及图10 可以看出，置换量会随着井底压差的增大而增大，当负压差超过下临界压差，则只发生溢流；当正压差超过上临界压差，则只发生井漏。本文所建立的漏喷函数与实验数据吻合度较高，对井底复杂的物质交换规律具有重要的理论意义。

4 结论

（1）建立了高压含气层钻井重力置换数学模型并进行了求解。结果表明，初始时刻对置换量影响最大的是裂缝两端的压差；气液重力置换界面稳定后，对置换量影响较大的因素依次为：裂缝宽度、裂缝高度、钻井液黏度、钻井液密度及裂缝长度。因此，保证井筒-地层处于近平衡状态是解决重力置换问题的有效方式。

（2）建立了高压含气层窄安全密度窗口重力置换问题漏喷函数并进行了实验验证，实验测试数据与理论计算数据吻合度较高。实验表明，随地层-井筒压差变化，裂缝中呈现出明显的3 个区间，分别为井漏区间、置换区间与井涌区间，存在3 种现象的两个临界点，分别为上临界点与下临界点。

（3）在钻遇窄安全密度窗口时，可利用本文所推荐的漏喷测试方法建立漏喷函数，确定钻穿窄安全密度窗口地层的最佳井底压力，以此设计钻井液密度、钻井液排量及井口回压等参数的最佳组合。

符号说明