基于虚拟质量的飞机颤振快速分析方法

王 斐，冉玉国，李秋彦

航空工业成都飞机设计研究所，四川 成都 610091

引言

气动弹性是一门多学科交叉的力学分支[1-2]，在传统飞机研制流程中，由于前期飞机结构布置、尺寸参数以及重量特性等输入条件不具备或存在诸多不确定性，气动弹性专业介入一般相对滞后。而在飞机研制后期，一旦暴露气动弹性稳定性问题，可设计空间有限，改进优化难度大，甚至可能导致设计方案被推翻等灾难性问题，付出人力、时间等巨大的代价[3]。

现代飞机由于不断追求减轻结构重量和提高飞行性能的目标，使得气动弹性稳定性问题变得愈加突出。这就要求气动弹性专业设计人员在飞机研制方案设计阶段尽早开展工作，避免对后续设计带来颠覆性问题。飞机研制是一项复杂的系统工程，在方案设计阶段，总体外形和结构布局不断迭代更新，没有足够的周期及成本用于对各个方案开展详细设计，不可能具备具体结构参数和重量数据。因此，该阶段气动弹性分析以定性为主，通过建立多学科综合分析与优化设计平台，开展关键参数敏感性分析，找出结构参数优化设计方向，可用于启发或指导后续详细设计工作。但在飞机设计方案阶段，如何针对大量不确定参数开展高效分析工作，以加快总体方案迭代进度，一直是困扰气动弹性设计师的难题[4-5]。

目前工程上气动弹性稳定性分析主要针对颤振问题，常用方法为模态法，即将分析模型转换到模态空间下求解，因此，模态分析是颤振分析的必要流程[6-8]。本文提出一种基于虚拟质量的飞机颤振快速分析方法，可减少模态分析次数，有效提升分析效率，满足方案设计阶段快速分析需求。

模态法采用一定数量低频固有模态表征结构位移响应，由于模态振型和频率都处于广义坐标系，与详细有限元模型无关，因此，可有效降低求解对象阶数，同时不会显著影响模型主要响应特性[9-10]。但是如果求解对象需要包含局部变形信息，选取的模态不能表征时，就可能导致计算错误。针对这类问题，虚拟质量法提供了一种解决办法，通过附加质量，获得局部参数变化引起的变形信息，提高分析准确性。虚拟质量法最早由Karpel 在子结构模态综合中提出[11]，后来推广到其他问题。如在“湿模态”求解中，虚拟质量可用以体现不可压缩流体对结构产生的作用，有效减少工作量[12-13]；在损伤识别中，基于虚拟质量法，有效增加测试数据量，避免结构附加真实物理元件的困难[14-15]。

1 理论基础

结构自由度下，气动弹性运动方程可表示为

虚拟质量法是在原结构中施加一块集中质量ΔM[16]，原结构去掉阻尼项的自由振动方程变为

通过模态分析，式（3）可表示为

用虚拟质量模态振型ΦFM替代原结构模态振型Φ，同时去掉虚拟质量，对质量矩阵、阻尼矩阵、刚度矩阵以及气动力矩阵进行广义化，自由振动方程变为

颤振方程变为

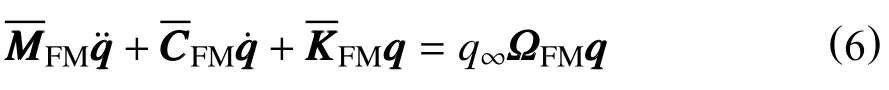
通过求解式（5）和式（6）可分别得到结构固有模态频率和颤振特性。

传统颤振分析流程需要先进行模态分析，然后，在此基础上开展颤振分析，对每一组结构参数都需要重复这个过程。按照上述方程推导，本文方法通过在原结构基准模型适当位置，施加集中质量，开展模态分析得到虚拟质量模态振型，将该振型作为固定的统一振型。虚拟质量施加位置一般选取靠近目标参数研究区域，同时不产生低频局部模态，大小最好与模型总质量在一个数量级。当结构参数局部改变时，不再开展模态分析，直接利用虚拟质量模态振型对模型质量矩阵、阻尼矩阵、刚度矩阵以及气动力矩阵进行广义化，进而求解颤振方程。本文方法在参数研究时只需开展一次模态分析，节省了模态分析时间，有效提升了颤振分析效率。

2 分析流程

虚拟质量法的基本思想是振型统一[17-18]。分析流程的第一步是在基准有限元模型上施加一个集中质量，作为虚拟质量，在此基础上开展模态分析，得到虚拟质量模态振型；然后，针对不同参数下的质量矩阵、阻尼矩阵、刚度矩阵以及气动力矩阵，采用虚拟质量模态振型进行广义化；最后，将广义化后的质量矩阵、阻尼矩阵、刚度矩阵以及气动力矩阵代入颤振方程，进而求解颤振特性。当结构局部参数发生小范围变化时，不需要再进行模态分析，本文算例变化范围为50%以内，直接采用该虚拟质量模态振型，更新质量矩阵、阻尼矩阵、刚度矩阵以及气动力矩阵即可。整个分析流程中只需要进行一次模态分析，针对不同结构参数，可直接开展颤振分析，具体流程见图1。

图1 分析流程图Fig.1 Analysis flow

3 算例仿真

3.1 模型基本参数

以全动翼面为对象，动力有限元模型如图2，大轴提供弯曲刚度，线弹簧和转轴的组合系统模拟旋转刚度。翼面采用单梁式结构，翼肋、主梁及蒙皮均采用玻璃钢复材，梁架网格间填充PMI 硬泡沫，基本参数如表1 所示。

图2 有限元模型Fig.2 Finite element model

表1 模型参数Tab.1 Model parameters

3.2 分析结果

采用虚拟质量为10 kg 的集中质量单元，施加位置如图2 所示。通过模态分析，可得到虚拟质量模态振型，如图3 所示。

图3 虚拟质量模态振型图Fig.3 Model shape of the fictitious mass

以模型旋转刚度为参数，研究旋转刚度对模型颤振特性的影响。旋转刚度由线弹簧和转轴的组合系统模拟，线弹簧基准值取1 000 N/mm，在此基础上旋转刚度分别变化20%和50%，刚度参数研究范围如表2 所示。

表2 旋转刚度参数变化范围Tab.2 Variation range of rotational stiffness

工程中结构模态分析方法一般采用MSC 公司的NASTRAN 软件[19-20]，针对表2 所示5 个刚度参数，分别采用NASTRAN 和本文方法得到前5 阶结构固有频率结果。分析结果表明，两种方法固有模态频率结果吻合非常好，最大误差不超过4%，见表3。以旋转刚度为参数开展研究，参数在50%～150%变化，虚拟质量模态振型可有效替代刚度变化对模态振型的影响，本文方法计算得到的结构固有频率与NASTRAN 计算结果基本一致。

表3 固有模态频率Tab.3 Natural mode frequency

针对旋转刚度的参数变化，进一步比较传统方法和本文方法的颤振特性计算结果。亚声速非定常气动力计算都使用ZONA6，采用非匹配点颤振分析，固定气流密度和马赫数，使用g 法求解颤振方程[21]，颤振计算采用前5 阶模态，计算马赫数为0.1，高度为0。不同旋转刚度计算结果表明，两种方法颤振特性计算结果基本一致，颤振速度最大误差为1.7%，颤振频率最大误差为2.1%，颤振速度都随着旋转刚度的增大而升高，见表4。可见本文方法计算精度可满足工程分析需求。

表4 颤振特性Tab.4 Flutter characteristics

以弹簧编号K1对应的颤振分析结果为例，对比两种方法得到的风速-阻尼图和风速-频率图，如图4～图7所示，两种方法得到的结构阻尼和频率随风速变化趋势基本一致，阻尼曲线由负到正的穿越都是第3 阶模态，其0 和2%阻尼值对应风速值相差非常小，频率曲线随风速的变化都表现为第1 阶模态和第3 阶模态的靠近，颤振耦合形式都是弯扭耦合。由此可见，本文方法得到的风速-阻尼、风速-频率图与传统方法基本一致，颤振特性相当，本文方法满足工程研制中颤振分析需求。

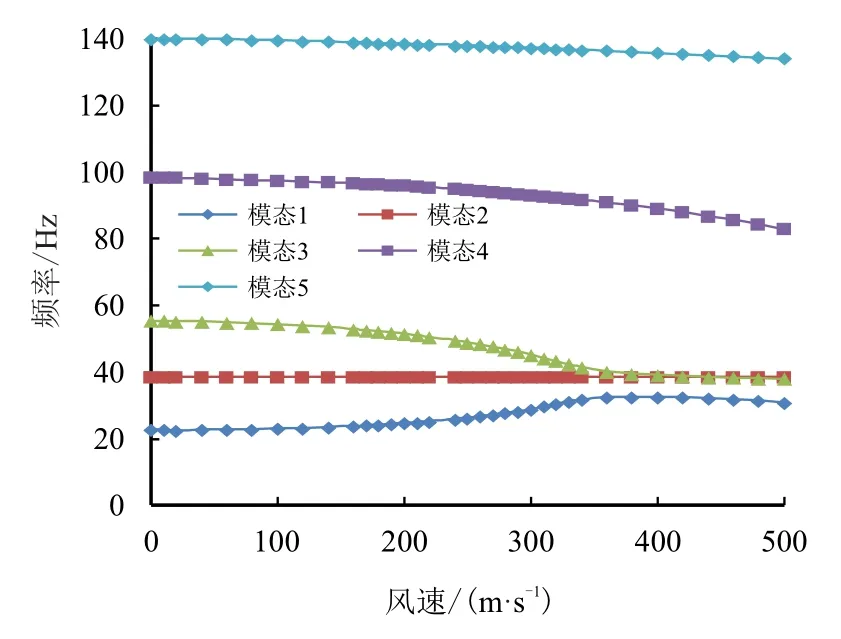
图4 传统方法风速-频率图Fig.4 Velocity vs.frequency graph of traditional method

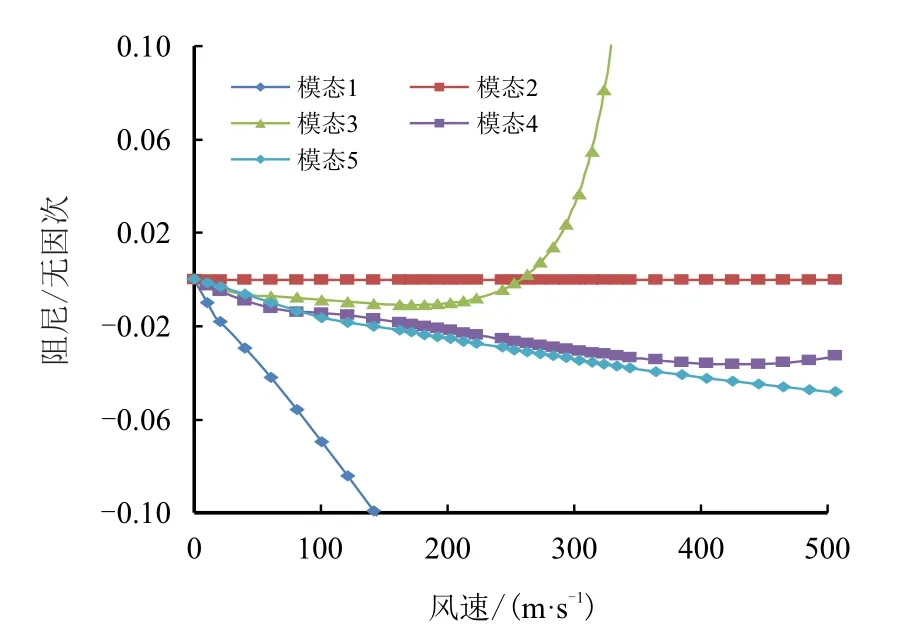
图5 传统方法风速-阻尼图Fig.5 Velocity vs.damping graph of traditional method

图6 本文方法风速-频率图Fig.6 Velocity vs.frequency graph of method method in this paper

图7 本文方法风速-阻尼图Fig.7 Velocity vs.damping graph of method method in this paper

4 结论

（1）结合工程需求，提出了一种基于虚拟质量的飞机颤振快速分析方法。该方法通过在原结构基准模型适当位置，施加一定大小的集中质量，开展模态分析得到虚拟质量模态振型，采用该振型作为统一振型，针对不同参数下的质量矩阵、阻尼矩阵、刚度矩阵以及气动力矩阵进行广义化，后续变参过程不再开展模态分析，直接求解颤振特性。

（2）在飞机研制初期参数敏感性研究过程中，基于虚拟质量的飞机颤振快速分析方法，采用虚拟质量模态振型，使得颤振方程的模态振型固定不变，显著提高了分析效率，并满足工程分析计算精度需求，为后续飞机详细设计和改进优化等工作提供了技术思路和解决方案。