基于反双曲正弦函数的循环本构模型

朱一林 ，王 凯

1.西南石油大学土木工程与测绘学院，四川 成都 610500

2.油气藏地质及开发工程国家重点实验室·西南石油大学，四川 成都 610500

3.四川大学建筑与环境学院，四川 成都 610065

引言

在航空航天、高速列车、核反应堆压力容器、金属冲模及电子封装等众多工程领域中，金属承载结构件在服役过程中通常要承受复杂循环载荷作用[1-3]。变形的循环累积引起的疲劳失效是金属构件最主要的一种失效模式。因此，材料的循环变形行为（尤其是棘轮行为）引起了国内外学者的广泛关注，并且在实验和本构模型研究方面取得了丰硕的成果。已有的循环本构模型可以分为基于“A-F”类随动硬化律的“A-F”类循环本构模型和多机制循环本构模型两类。在多机制模型中，非弹性应变由两种机制产生，并且需要对材料参数的取值给出附加限定以确保热力学相容性[4-6]。1966 年，Frederick 等[7]将Prage 线性随动硬化律[8]进行改进，引入了一个动态恢复项，提出了“A-F”类随动硬化律，并基于此建立了“A-F”类循环本构模型。“A-F”类循环本构模型中引入的动态恢复项使其具有了描述材料棘轮行为的能力。尽管其预测的棘轮演化速率为常数，总是过高地预测了棘轮效应（特别是对多轴加载情况），但模型中非弹性应变仅由一种机制产生，物理意义明确，理论形式也更为简单，并且可自动保证热力学相容性。因此，近几十年来众多学者对“A-F”类随动硬化律进行了改进和发展，并建立了众多“A-F”类循环本构模型。“A-F”类随动硬化模型是目前应用最广泛的循环本构模型，根据背应力的演化特性，其又可分为“Chaboche”类循环本构模型和“Ohno-Wang”类循环本构模型。为改善对棘轮行为的描述能力，Chaboche 等[9]将背应力分解为4 项，并且令每项都服从“A-F”类随动硬化律，建立了一个叠加模型（Chaboche 模型I）。尽管对棘轮效应的预测能力得到了显著提升，但Chaboche模型I 依然高估了棘轮应变的演化（尤其是多轴情况）。为进一步提高模型的预测能力，Chaboche[10]在Chaboche 模型I 的第四背应力分量的动态恢复项中引入了一个门槛值的概念，提出了Chaboche 模型II，但该模型参数确定较为复杂，对材料的单轴和多轴棘轮行为的描述同样不能很好地兼顾。此后众多学者对Chaboche 模型I 和II 又做了改进，建立了众多的“Chaboche”类循环本构模型。为进一步改善本构模型对棘轮变形预测过高的缺点，Ohno等[11-12]将Chaboche 模型II 中动态恢复项的门槛值概念进一步推广，提出了动态恢复完全被激活的临界状态的概念，采用多项叠加的分段线性随动硬化律来模拟应力-应变曲线，建立了Ohno-Wang 模型I 和Ohno-Wang 模型II。此后，Abdel-Karim 等[13]、Kang 等[14]以及Yu 等[15]将Ohno-Wang 模型继续修正，提出了多种“Ohno-Wang”类循环本构模型，并且对材料在特定工况下的棘轮行为均可给出较为合理的描述。

为描述材料的循环大变形行为，有学者将上述在小变形框架下建立的“A-F”类循环本构模型进行了大变形拓展[16-19]。

已有实验结果[1]表明，金属材料在循环大变形时存在瞬态包辛格效应，即：如果产生反向屈服的应变较大，反向屈服时的塑性模量大于单调加载时的塑性模量（图1）[20]；与之相反，如果产生反向屈服的应变较小，瞬态包辛格效应会减弱，有时反向屈服时的塑性模量甚至要小于单调加载时的塑性模量（图2）[21-22]。

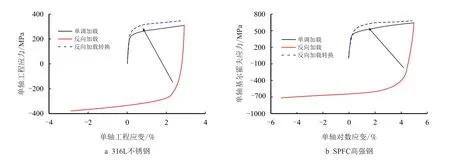
图1 单调和大应变反向加载时塑性模量的比较[20]Fig.1 Comparison of plastic moduli obtained during the monotonic and large strain reverse loading tests

图2 单调和小应变反向加载塑性模量的比较[21-22]Fig.2 Comparison of plastic moduli obtained during the monotonic and small strain reverse loading tests

众所周知，材料在循环加载过程中还可能伴随损伤的产生和热-力耦合作用，而对应力-应变滞回环的描述是合理预测材料热-力-损伤耦合变形的最关键的基础。然而，目前已有的循环本构模型大都仅关注对材料棘轮变形行为的描述，并没有考虑单调和循环加载时塑性模量的不同，因而对循环变形过程中的应力-应变滞回环尚不能给出合理的预测结果。为此，在前期的工作中，Zhu 等提出了一个改进的Chaboche 随动硬化律[1]，在演化方程中考虑了单调和循环变形时塑性模量的差异，对应力-应变滞回环可以给出较为合理的描述[1]。该硬化律是基于自然对数函数来进行构建。本文利用同样的思想，基于反双曲正弦函数形式，提出了改进的Chaboche 类随动硬化律，并基于此建立了循环本构模型，验证了其对材料棘轮行为及循环变形过程中应力-应变滞回环的预测能力。

1 本构模型

常用的大变形本构框架有两种，即：基于变形梯度张量F乘法分解的超弹性框架和基于伸长张量D加法分解的次弹性框架。在超弹性框架中建立本构方程需要引入额外的内变量，数值实现较为复杂。而在次弹性框架中建立的本构方程形式非常简单，其本质是将小变形下导数形式的演化方程改写成合适的客观率形式直接进行推广。Xiao和Bruhns[23-25]的工作已经证明，只有采用对数客观率（下文简称为对数率），本构方程才是严格自洽的。因此，本文拟基于对数率在次弹性框架下建立本构方程，本构方程由运动学方程、主控方程和演化方程3 部分组成。

1.1 运动学方程

参照Zhu 等[1]的工作，次弹性大变形框架下的运动学方程包括

式中：hHencky 对数应变（对数应变），无因次。

本构方程为对数率形式。对数应变的对数率与伸长张量等价，即

对于任意一个对称二阶张量的对数率可表示为

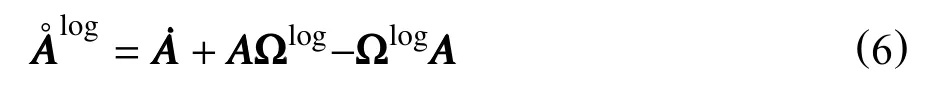
式中：A任意的一个二阶对称张量，无因次；

Ωlog反对称的对数自旋张量，无因次，其定义详见文献[23-25]。

1.2 主控方程

通常，金属材料的弹性变形在总变形中占比很小。因此，可将对数应变和伸长张量进行加法分解

式中：he弹性对数应变，无因次；

hp塑性对数应变，无因次。

式中：De弹性伸长张量，s-1；

Dp塑性伸长张量，s-1。

进一步，可假设弹性伸长张量De和弹性应变he的对数率等价，即

通常，弹性应变he可由胡克定律进行表征

式（10）的对数率形式可表示为

由式（11）的逆形式可得次弹性关系

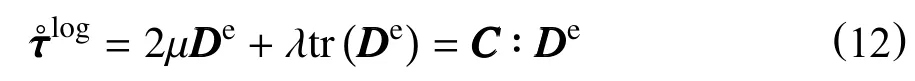
式中：C四阶弹性张量，MPa；

本文非弹性应变假设为率无关形式，可以通过冯·米塞斯屈服面定义。冯·米塞斯屈服面可表示为

基于关联塑性流动，塑性伸长张量可表达为

式中：N屈服面Fy的单位法向张量，无因次，其定义为

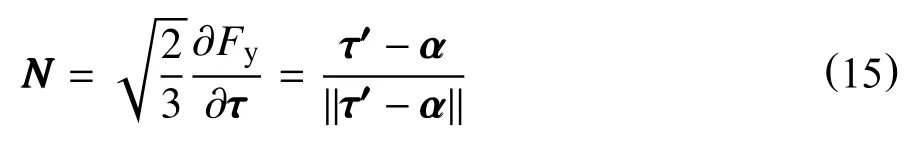
1.3 演化方程

参照文献[9]，将背应力α 分解为3 部分

其中，α1，α2和α3为长程、中程和短程背应力分量，分别对应于材料的准线性、低非线性和高度非线性硬化部分。

长程和中程背应力分量的演化方程为

显然，q可表征材料在变形过程中的最大塑性应变。

在单调加载条件下，式（18）是可以积分的，其积分形式为反双曲正弦函数

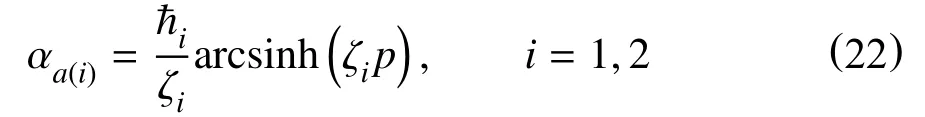
如前文所述，不同于大变形时的瞬态包辛格效应，材料在变形较小时，瞬态包辛格效应会减弱，甚至有反向屈服塑性模量降低的现象。为了描述这一行为，短程背应力的演化可表示为

在单调加载时，该式依然是可以积分的，其积分结果仍然为反双曲正弦形式

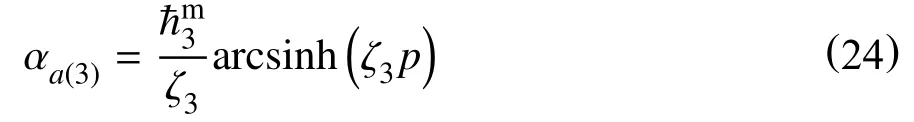
对于各向同性硬化，本文引入了Chaboche[12]提出的指数演化形式，即

1.4 参数讨论

讨论本文提出的本构模型的描述能力时所用的材料参数如表1 所示。表1 中所用的材料参数是用来考察SPFC 高强钢在应变循环加载下的应力-应变滞回环响应的。另外，为了消除各向同性硬化的对模型预测能力的影响，β 的取值设置为0，并且Q0和Qsa的取值设置相同。

表1 SPFC 高强钢材料参数Tab.1 Material parameters for SPFC high strength steel in the proposed model

1.4.1 应力-应变滞回环

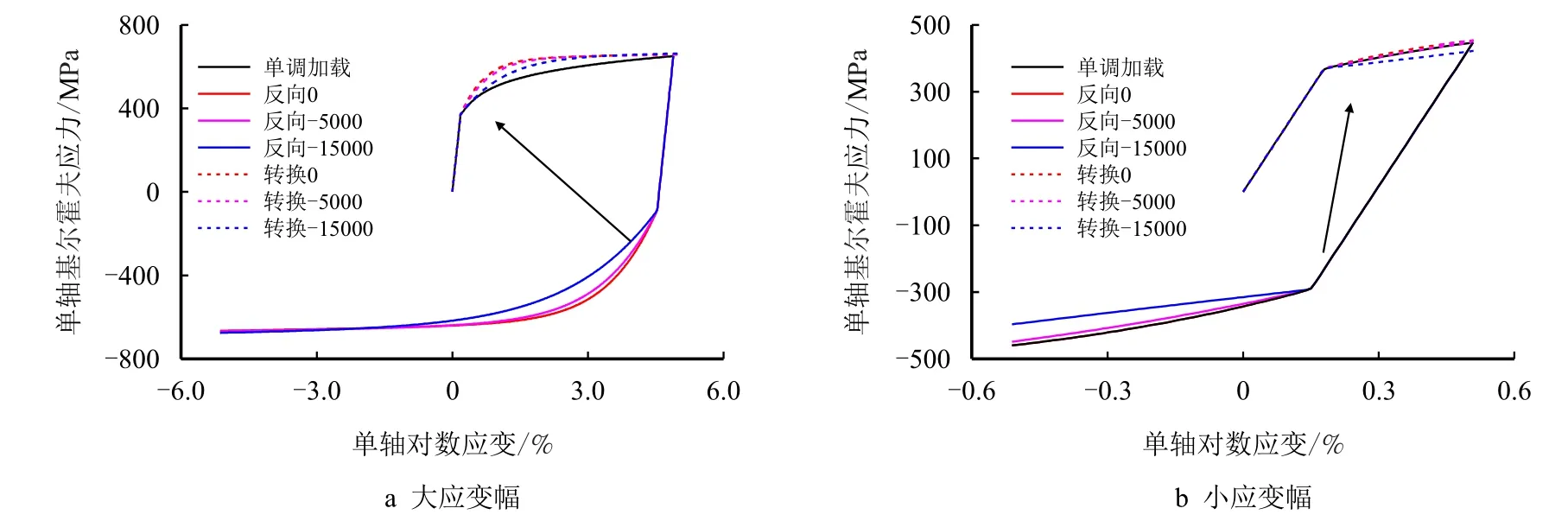
图3 不同取值时预测的对称应变循环应力-应变响应Fig.3 Stress-strain responses with difference?in symmetric strain-controlled cyclic tests

1.4.2 棘轮变形

其他参数保持如表1 所示不变，只改变m1,2的取值，模型预测的棘轮应变响应（加载的名义平均应力为100 MPa，名义应力幅为400 MPa）如图4 所示。可见，通过调整m1,2的取值可达到调控棘轮应变演化的效果。图4 中的棘轮应变定义为

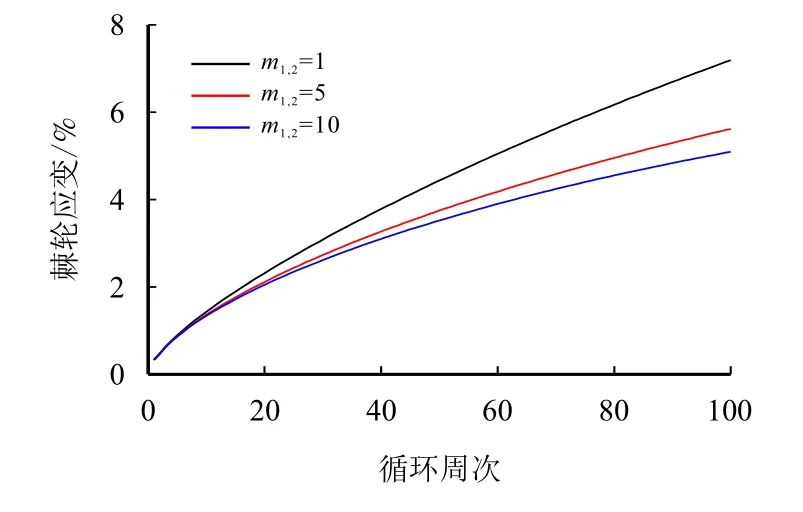
图4 不同m1,2 取值时棘轮应变响应Fig.4 Effect of m1,2 on the predicted ratchetting strain

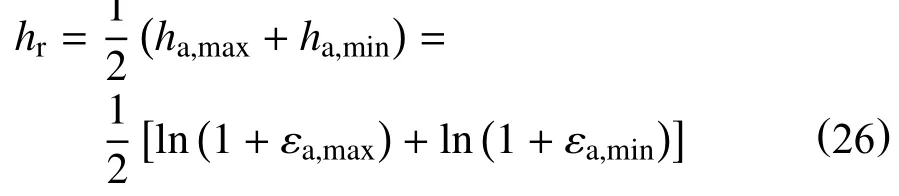
式中：

ha,max,ha,min一个循环中最大、最小的对数应变，无因次；

εa,max,εa,min一个循环中最大、最小的工程应变，无因次。

2 模型验证

为体现本文模型的优越性，将模拟结果跟已有经典模型的模拟结果也做了对比。为简便起见，这里只考虑了跟大变形Karim-Ohno 模型（Karim 等首次提出，Zhu 等[17]在大变形框架下做了拓展）的对比。该模型的随动硬化律为

除随动硬化律外，上述两个本构模型其余的本构方程均相同。

2.1 U71Mn 轨道钢的变形行为

为考察对棘轮变形的模拟结果，首先对Kang等[26]的实验结果进行模拟。实验材料为U71Mn 轨道钢。所用试样为直径10 mm、工作段长度25 mm的圆棒试样。实验包括单轴拉伸和应力循环变形。单轴拉伸实验的工程应变率为0.2%/s。循环变形实验工况有3 类：（1）单级非对称应力循环工况（工况A），主要用于考察材料在单级加载下的棘轮行为；（2）固定应力幅的多级非对称应力循环工况（工况B），主要考察不同平均应力对材料棘轮变形的影响；（3）固定平均应力的多级非对称应力循环工况（工况C），用于考察不同平均应力幅对材料棘轮变形的影响。各工况具体加载水平详见表2。另外，应力循环变形实验中采用名义应力控制，加载率为51 MPa/s。

表2 U71Mn 轨道钢应力循环实验加载情况Tab.2 Load cases used in the cyclic stressing tests of U71Mn rail steel

利用本文提出的模型进行模拟时所采用的材料参数如表3 所示。其中，m1和m2通过单级非对称应力循环实验结果确定，其余参数均从单调拉伸曲线确定。Zhu 等[17]提出的大变形Karim-Ohno 模型的材料参数如表4 所示。

表3 本文模型中U71Mn 轨道钢材料参数Tab.3 Material parameters for U71Mn rail steel in the proposed model

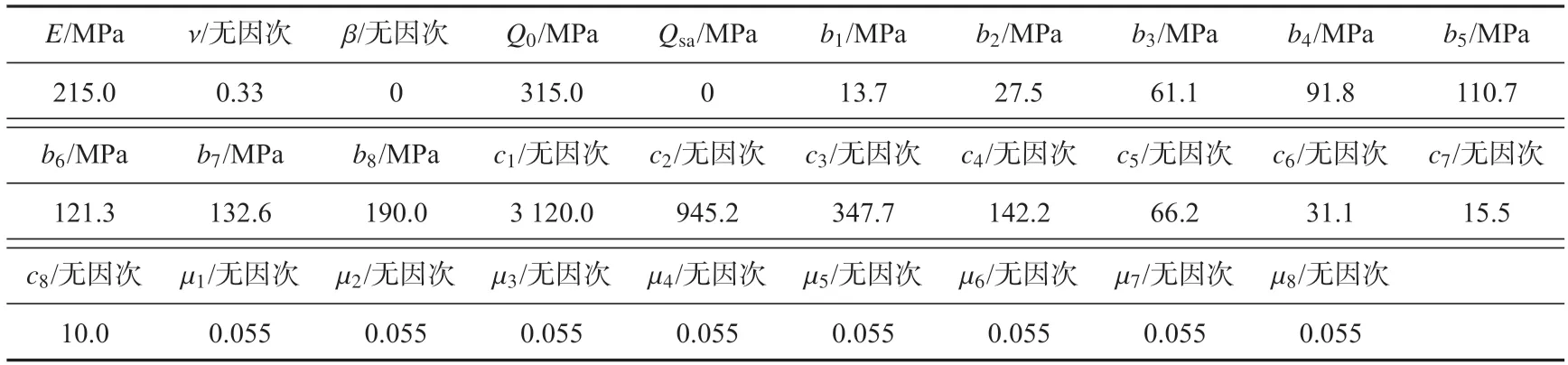
表4 U71Mn 轨道钢材料参数（大变形Karim-Ohno 模型参数）Tab.4 Material parameters for U71Mn rail stee（lThe finite Karim-Ohno model）

另外，在Kang 等[26]的实验中，U71Mn 轨道钢表现出的材料各向同性硬化不明显。为简化计算，模拟时均忽略各向同性硬化效应，即设置β 为0。

图5 给出了U71Mn 轨道钢在单调拉伸实验时的应力-应变响应及其模拟结果。可以看出，本文提出的模型和大变形Karim-Ohno 模型均可对材料的单调加载响应给出合理的描述。

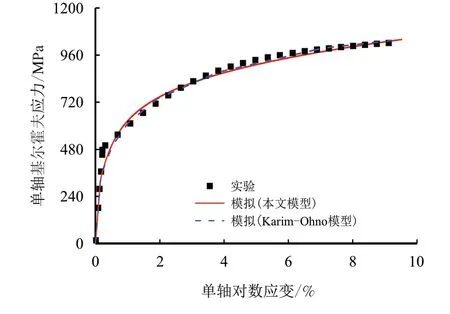
图5 U71Mn 轨道钢在单调拉伸时的应力-应变曲线Fig.5 Experimental and simulated tensile stress-strain curves of U71Mn rail steel

图6～图8 给出了U71Mn 轨道钢在单级和多级非对称应力循环加载时候的应力-应变响应。可以看出，两种本构模型均可合理预测材料的单级和多级棘轮行为及平均应力和应力幅对棘轮行为的影响；但只有本文模型可合理表征应力循环过程中的应力-应变滞回环，而大变形Karim-Ohno 模型严重过高地预测了应力-应变滞回环的面积。

图6 U71Mn 轨道钢在工况A 中的应力-应变实验和模拟Fig.6 Experimental and simulated stress-strain curves of U71Mn rail steel for working condition A

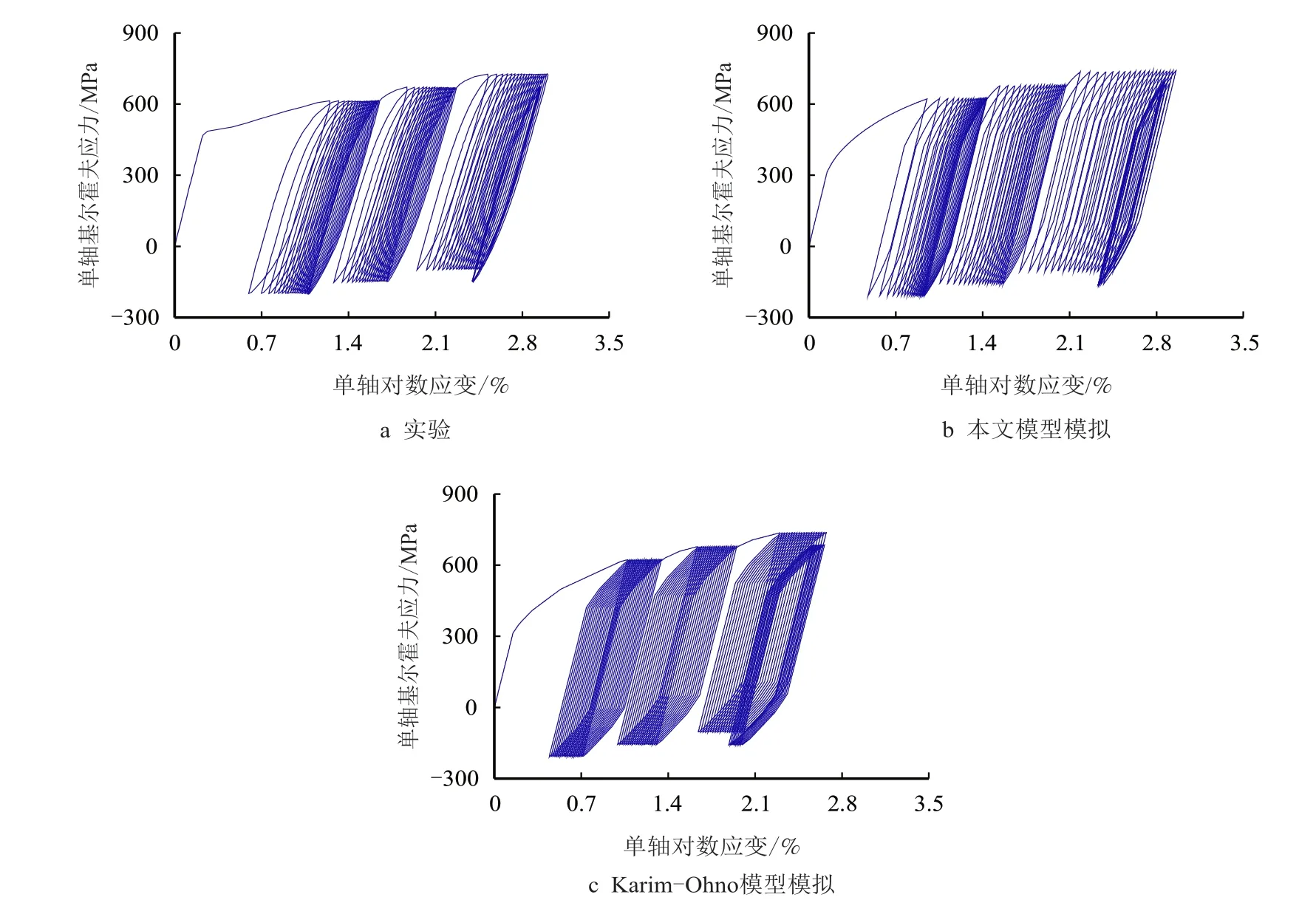
图7 U71Mn 轨道钢在工况B 中的应力-应变实验和模拟Fig.7 Experimental and simulated stress-strain curves of U71Mn rail steel for working condition B

图8 U71Mn 轨道钢在工况C 中的应力-应变实验和模拟Fig.8 Experimental and simulated stress-strain curves of U71Mn rail steel for working condition C

2.2 SPFC 高强钢的变形行为

为考察模型对瞬态包辛格效应的预测能力，进一步研究了SPFC 高强钢在大应变循环实验时的变形行为[20]。实验工况包括：（1）单级对称应变循环加载（工况D）；（2）单级非对称应变循环加载（工况E）；（3）多级非对称应变循环加载（工况F）。需要指出的是，实验中的加载方式为真应变控制。各工况具体加载水平详见表5。

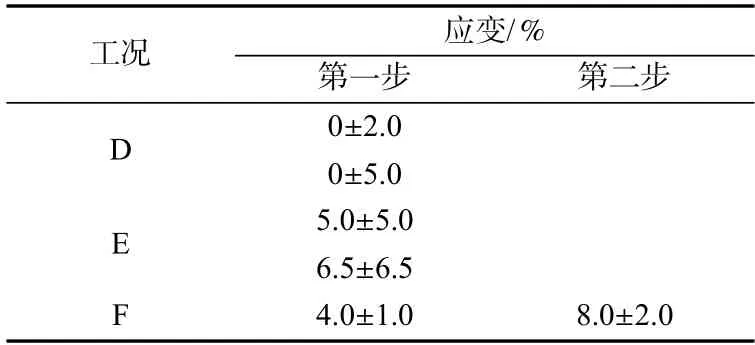
表5 SPFC 高强钢应变循环实验加载工况Tab.5 Load cases in strain-controlled cyclic tests of SPFC high strength steel

为突出本文模型的预测能力，同样将模拟结果与大变形Karim-Ohno 模型的模拟结果进行对比。两个本构模型所用材料参数分别如表1 和表6 所示。两个模型对SPFC 高强钢在大应变循环加载下的应力-应变响应的模拟结果见图9～图11。

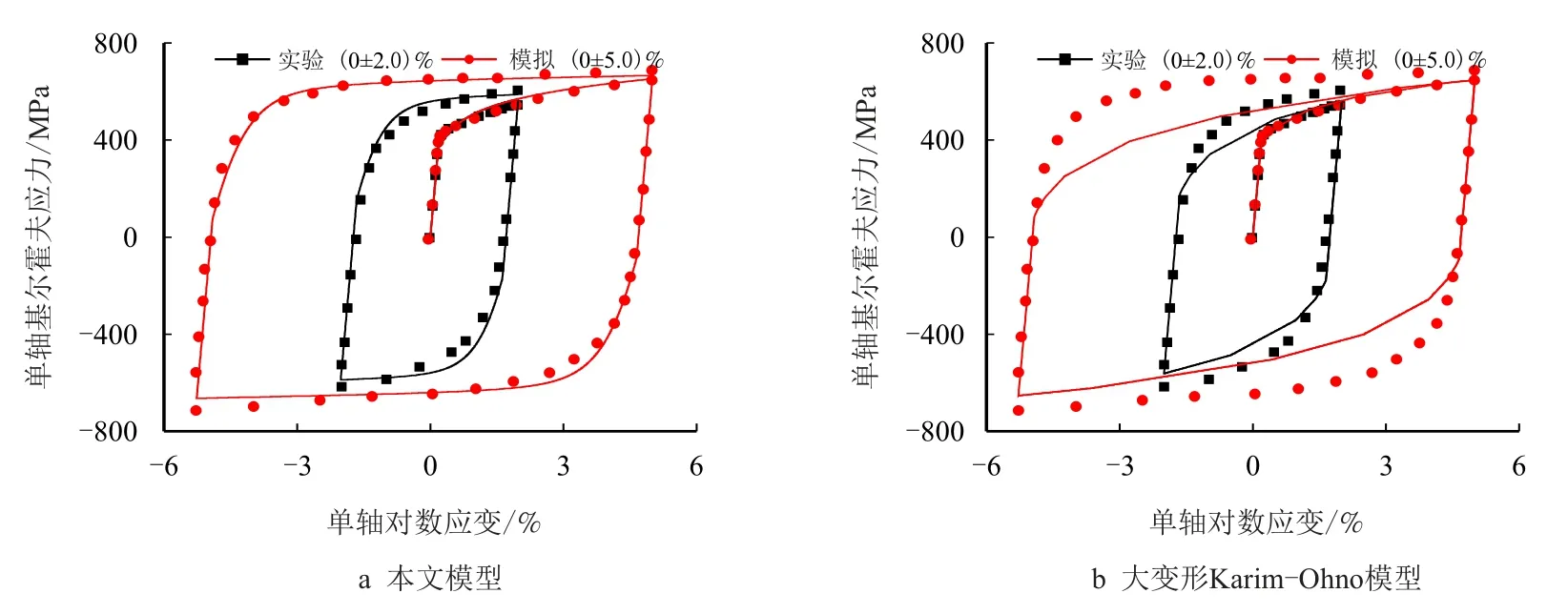
图9 两种模型对SPFC 高强钢在工况D 中的应力-应变曲线的模拟Fig.9 Simulation of stress-strain curve of SPFC high strength steel under working condition D by two models

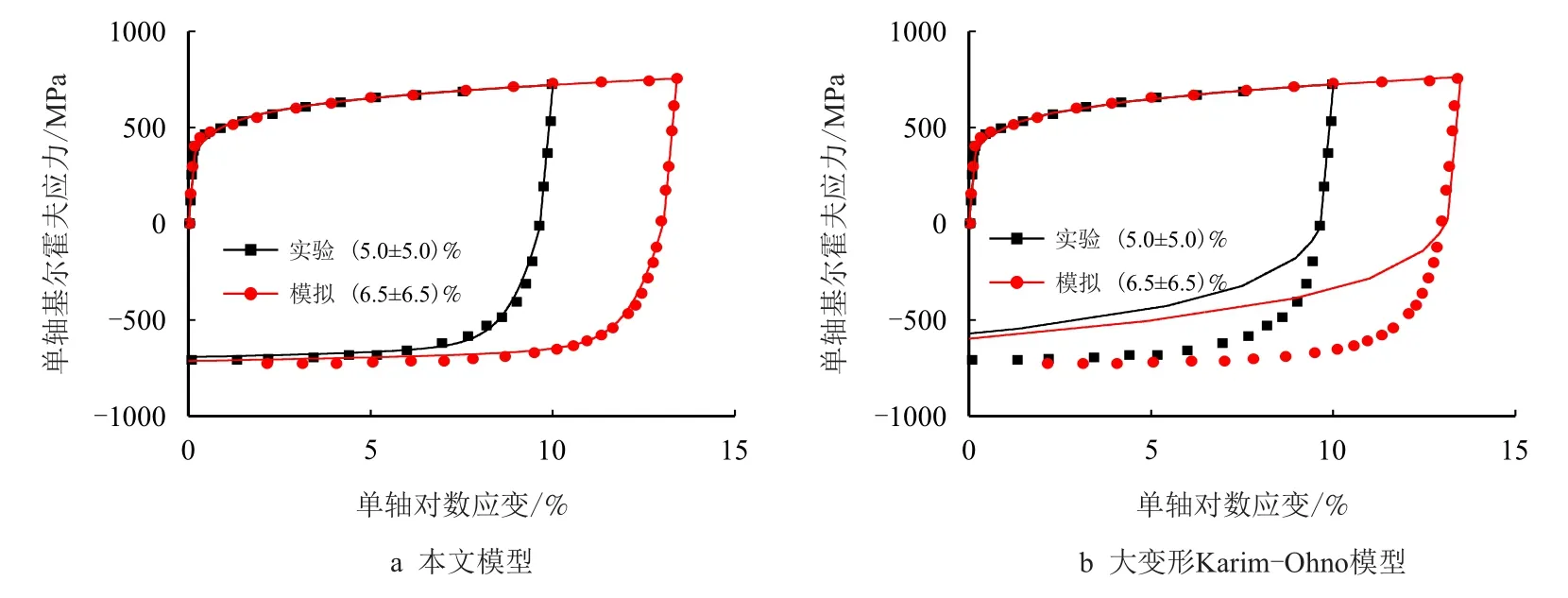
图10 两种模型对SPFC 高强钢在工况E 中的应力-应变曲线的模拟Fig.10 Simulation of stress-strain curve of SPFC high strength steel under working condition E by two models

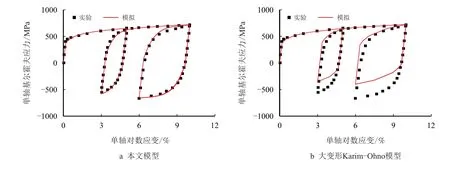
图11 两种模型对SPFC 高强钢在工况F 中的应力-应变曲线的模拟Fig.11 Simulation of stress-strain curve of SPFC high strength steel under working condition F by two models

表6 SPFC 高强钢材料参数（大变形Karim-Ohno 模型）Tab.6 Material parameters for SPFC high strength stee（lthe finite Karim-Ohno model）

由图9～图11 可以看出，本文模型能很好地描述大变形反向加载时材料的瞬态包辛格效应；而Karim-Ohno 模型并不能对此现象给出合理预测。

另外，本文基于反双曲正弦函数的本构模型与Zhu 等[1]提出的基于对数函数的本构模型对棘轮变形和应力-应变滞回环具有相近的预测能力。

3 结论

（1）将传统Chaboche 随动硬化律进行改进，提出一个可合理描述材料棘轮行为和应力-应变滞回环的新的随动硬化律。该硬化律在单调加载时是可积的，积分形式为反双曲正弦函数。

（2）所提出的随动硬化律材料参数非常便于确定，描述单调加载响应、棘轮应变演化和滞回环形状的材料参数相互不耦合，可以通过不同的实验工况确定。

（3）基于对数应力率，在大变形框架下建立了循环本构模型。模型可以很好地对材料的单调加载变形行为、棘轮行为以及循环变形过程中的应力-应变滞回环做出描述。