基于广义最大周向应变准则的断裂特性研究

华 文，潘 鑫，淦志强，董世明

深地科学与工程教育部重点实验室·四川大学，四川 成都 610065

引言

断裂力学的重要任务之一就是建立适当的断裂准则，对含裂纹构件材料的断裂行为进行理论评估及寿命预测。

在过去的几十年里，学者们曾先后提出了多种复合型断裂准则用于预测含裂纹的线弹性材料的断裂行为[1]。就脆性或准脆性材料的I～II 复合型断裂而言，使用较为频繁的主要有：最大周向应力（MTS）准则[2]，最小应变能密度因子（SED）准则[3]和最大能量释放率（MERR）准则[4]。

尽管这些经典的仅考虑了裂纹尖端应力奇异项的断裂准则在脆性材料宏观断裂特性分析中起到了重要的作用；然而，大量的试验结果表明，裂纹尖端的非奇异常数项（T应力）对脆性或准脆性材料的断裂特性有较大的影响，基于传统断裂准则（如MTS，SED，MERR）的理论值与试验值之间仍然存在有较大的差异[5-11]。因此，一些学者开始着手考虑增加Willimas[12]级数展开式中的项数以提高理论预测值的精度。

Smith 等[5]考虑了T应力的影响，对传统的最大周向应力准则进行了修正，提出了广义最大周向应力（GMTS）准则。

Ayatollahi 等[13]同时考虑了Williams 级数展开式中的前3 项，对最大周向应力准则进行了进一步的改进，提出了修正的最大周向应力（MMTS）准则，并成功地解释了基于三点弯曲试件的试验结果的尺寸效应。

赵艳华和徐世烺等[14]引入了裂纹尖端的T应力项，将偏斜应力张量的第二不变量J2作为了断裂的判据，提出了I～II 复合型裂纹脆性断裂的最小J2准则。

Ayatollahi 等[15-16]同时考虑了Williams 级数展开式中的应力奇异项和非奇异常数项对最小应变能密度因子准则进行了修正，提出了广义最小应变能密度因子（GSED）准则和广义平均应变能密度因子（GASED）准则。

与基于应力和能量的断裂准则类似，研究者们也曾先后提出了多种基于应变的复合型断裂准则[17-20]。

Chang[18]于1981 年提出了最大周向应变准则，并将其用于分析平面应力状态下中心裂纹板的断裂问题。邓宗才等[20]在Chang[18]的基础上对最大周向应变准则进行了进一步的拓展，使得该准则可以适用于平面应变问题。

Ayatollahi 等[21]最早就开始考虑裂纹尖端T应力的影响，对最大周向应变（MTSN）准则进行了简单的改进，分析了中心裂纹板试件的断裂问题。而后，Mirsayar[22]提出了修正的最大周向应变（EMTSN）准则，并利用该准则对有机玻璃，岩石等脆性或准脆性材料的断裂行为进行了理论预测。然而，Mirsayar[22]提出的最大周向应变准则是在平面应力状态下推导出来的，不能直接用于平面应变问题的断裂分析；此外，他在该文中所有的讨论分析都是基于错误的参数[22-23]。

基于此，作者在之前的研究中对Mirsayar[22]的错误参数进行了进一步的修正，并给出了平面应力和平面应变条件下广义最大周向应变（GMTSN）准则的统一表达式[23]。为了进一步探究T应力对中心裂纹圆盘（CCBD）试件I～II 复合型断裂特性的影响规律，本文基于之前的研究基础，利用广义最大周向应变准则讨论和分析了T应力，裂纹尖端的临界距离r0和泊松比ν 对中心裂纹圆盘试件的裂纹扩展路径以及临界应力强度因子的影响规律。同时，利用广义最大周向应变准则对基于中心裂纹圆盘试件的断裂试验结果进行了评估，明确T应力对中心裂纹圆盘试件复合型断裂特性的影响，进一步验证该准则的适用性。

1 修正的广义最大周向应变准则

如图1 所示，在二维线弹性断裂力学中，I～II 复合型加载条件下裂纹尖端的应力场可由Willimas[12]级数展开式表示为

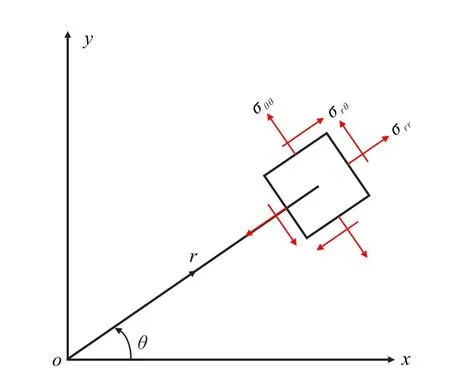
图1 裂纹尖端应力场示意图Fig.1 Diagram of the stress field around the crack tip

对于平面应力问题有σzz=0；而平面应变问题，σzz=ν(σrr+σθθ)，其中ν 为泊松比。根据Hooke定律，裂纹尖端的周向应变εθθ可统一表示为[23]

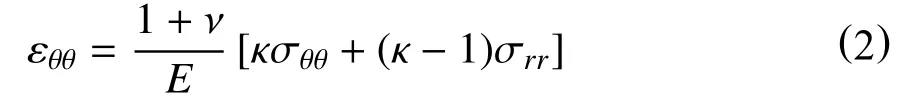
将应力分量σθθ，σrr代入式（2）后，并化简可以得到

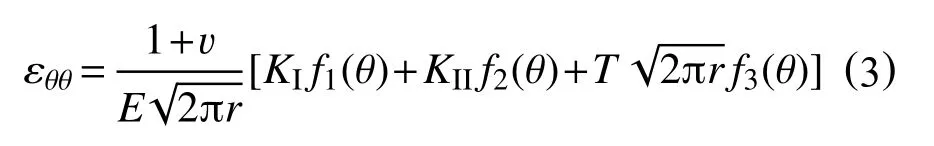
其中，系数f1，f2和f3的表达式为

根据广义最大周向应变准则[23]，裂纹将沿着最大周向应变的方向（θ0）起裂，并且在距离裂纹尖端临界距离r0处的最大周向应变达到某一临界值εt时，裂纹发生失稳扩展。因此，广义最大周向应变准则可表示为

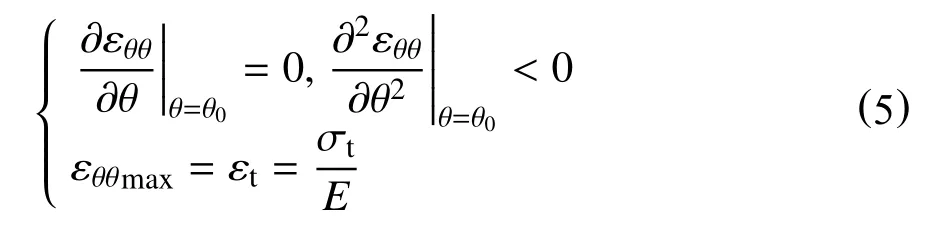
将式（3）代入式（5）并化简可得

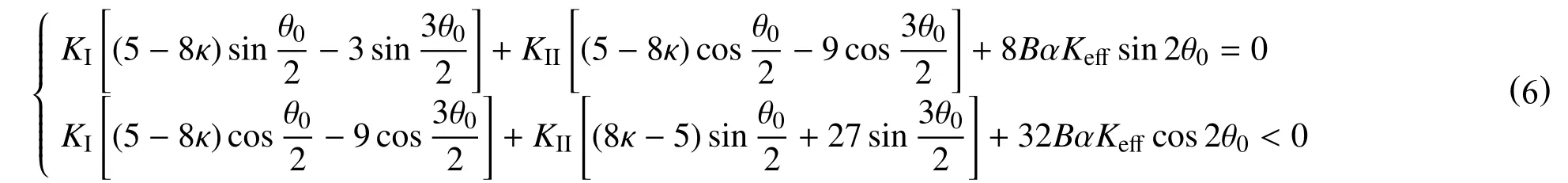
其中，系数B，α 和Keff_的定义如下

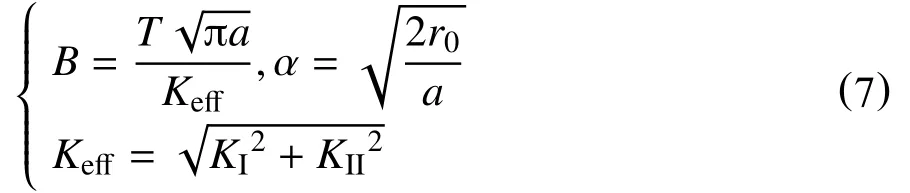
裂纹开裂角θ0可由式（6）计算得到，将得到的开裂角θ0代入式（3）并结合式（5）可得

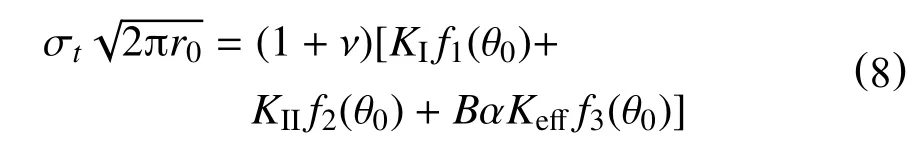
纯I 型加载时，有：KI=KIC，KII=θ0=0，故而式（8）可化简为

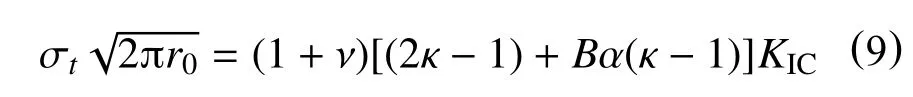
进而得到

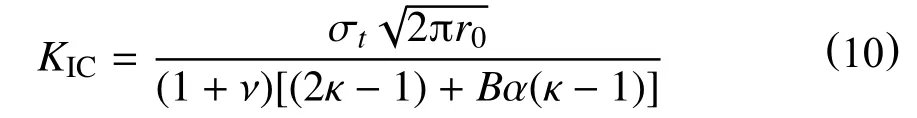
需要指出的是，此时的Bα 应满足小于(2κ+1)/8的条件，将式（9）代入式（8）式并化简可得

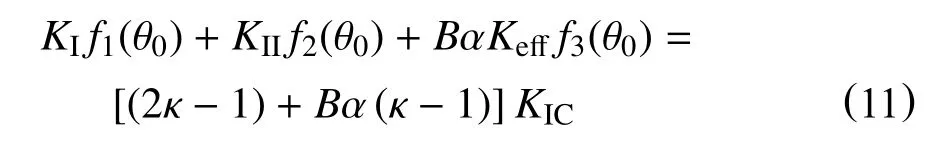
因此，KIf/KIC，KIIf/KIC的比值可表示为

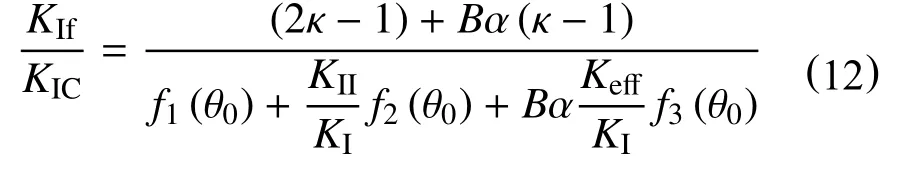
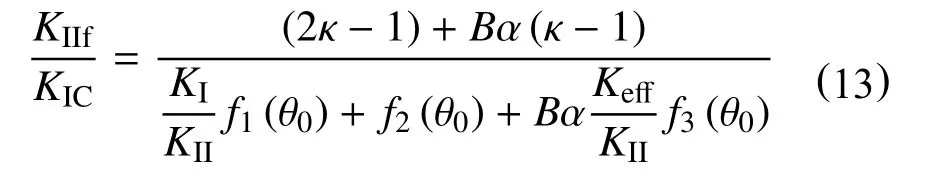
如果已知ν，KI，KII，T，r0等相关参数，我们就可以使用式（6）计算裂纹开裂角θ0，并利用（12）式和（13）式计算I～II 复合型断裂韧度的比值KIf/KIC，KIIf/KIC。

为了明确T应力以及泊松比等参数对裂纹开裂角以及复合型断裂韧度的影响，本文将基于中心裂纹的圆盘试件，利用广义最大周向应变准则，讨论T应力以及泊松比等对I～II 复合型断裂特性的影响规律。

2 T 应力及泊松比对I～II 复合型断裂特性的影响

为了利用广义最大周向应变准则对脆性或准脆性材料的断裂行为进行理论预测分析。

首先，我们应该计算出试样的断裂参数KI，KII和T。

如图2 所示，中心裂纹圆盘试件因其构型简单，试件加工方便，可以通过改变加载方向与裂纹面的夹角（加载角），从而方便地实现纯I、纯II 以及I～II复合型加载方式；并且其应力强度因子和T应力均存在解析公式[24-25]。

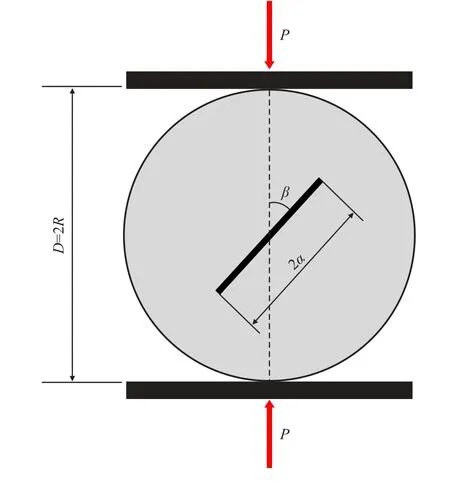
图2 中心裂纹圆盘试件受力示意图Fig.2 Diagram of the CCBD specimen under compression

因此，被广泛地用于脆性或准脆性材料断裂韧度的测试。

半径为R，厚度为t，裂纹长度为2a 的中心裂纹圆盘试件在径向承受集中荷载P的作用，其应力强度因子KI，KII和T应力可以表示为如下的形式

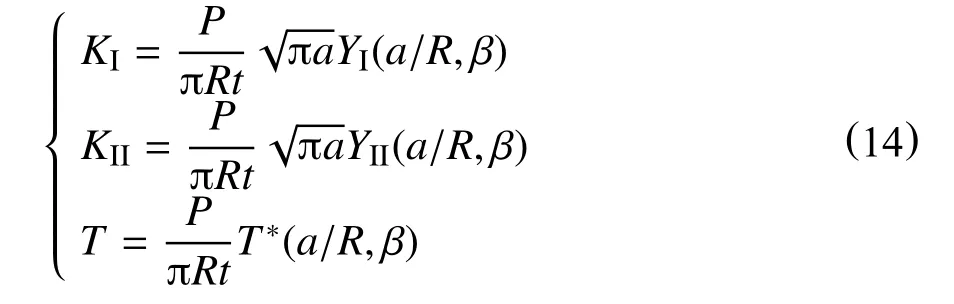
图3 给出了拉-剪状态下中心裂纹圆盘试件的无量纲断裂参数YI，YII和T*。从图3 可以看出，随着加载角的增加，I 型无量纲应力强度因子YI逐渐减小，而II 型无量纲应力强度因子YII逐渐增大。

近年来，各类伺服控制系统广泛应用于智能制造、工业机器人、精密数控装备等领域。在高性能伺服系统中，电机速度反馈的实时性和精度是影响伺服系统控制性能的决定性因素。在当前的工程应用中，因受限于测速传感器成本和分辨率以及无传感器控制技术依赖于复杂、高阶的电机模型和负载特性，再加上环境扰动、复杂工况等因素的影响，宽范围、高精度电机转速测量问题仍是学术界和工程界具有挑战性的研究重点。

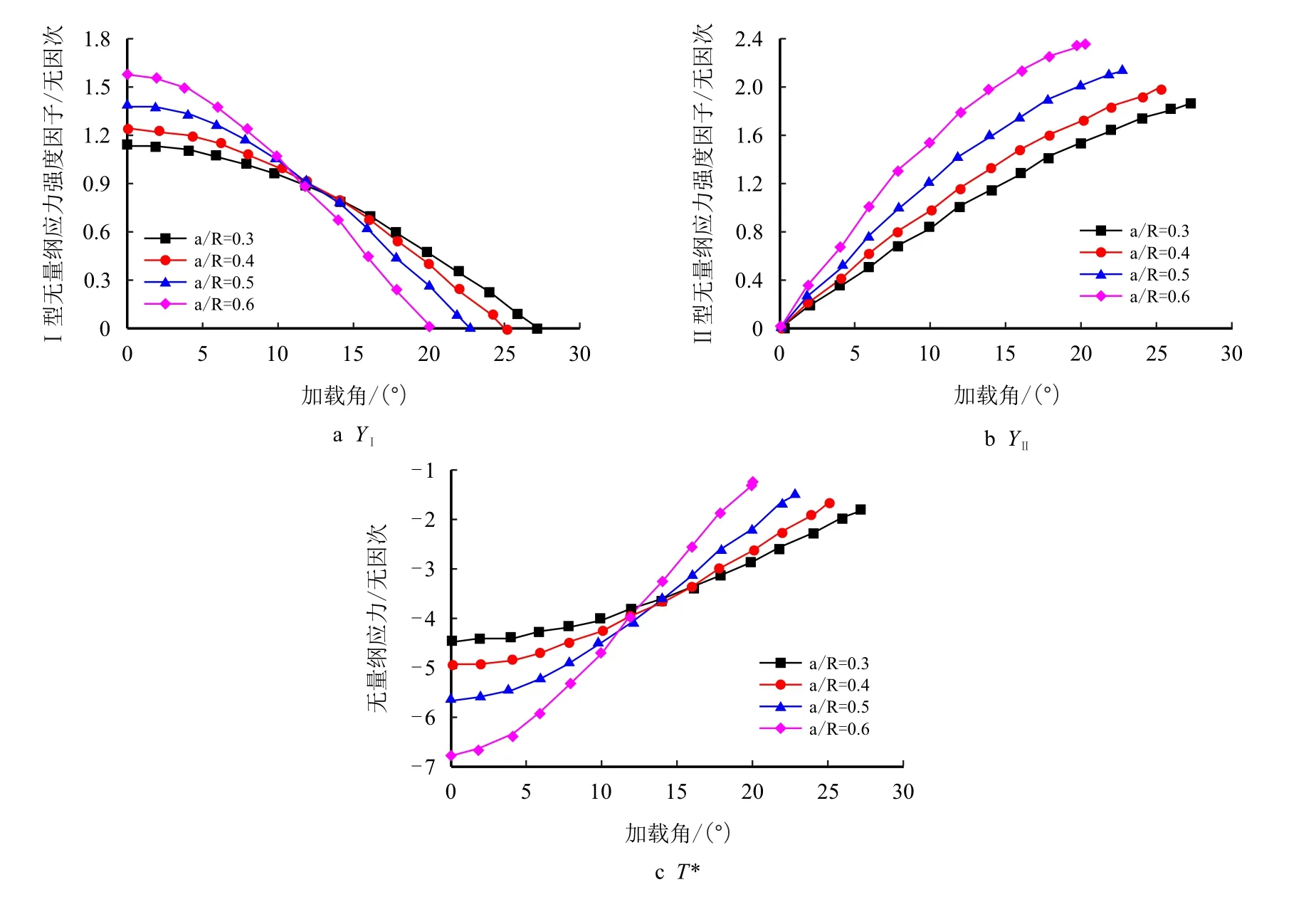
图3 中心裂纹圆盘试件的无量纲断裂参数[23]Fig.3 The dimensionless fracture parameters for CCBD specimens[23]

无论是纯I 型、纯II 型以及I～II 复合型裂纹，无量纲T应力均为负值，对于给定的裂纹长度，无量纲T应力的绝对值总是随着加载角的增大而减小。

如果这些断裂参数均已知，求解裂纹开裂角θ0的表达式（6）就可以用无量纲断裂参数重新表示为

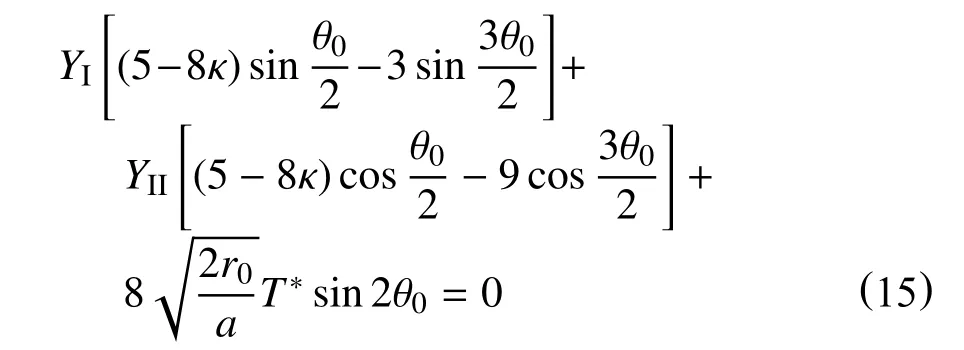
同样地，KIf/KIC和KIIf/KIC的比值也可用无量纲断裂参数表示为

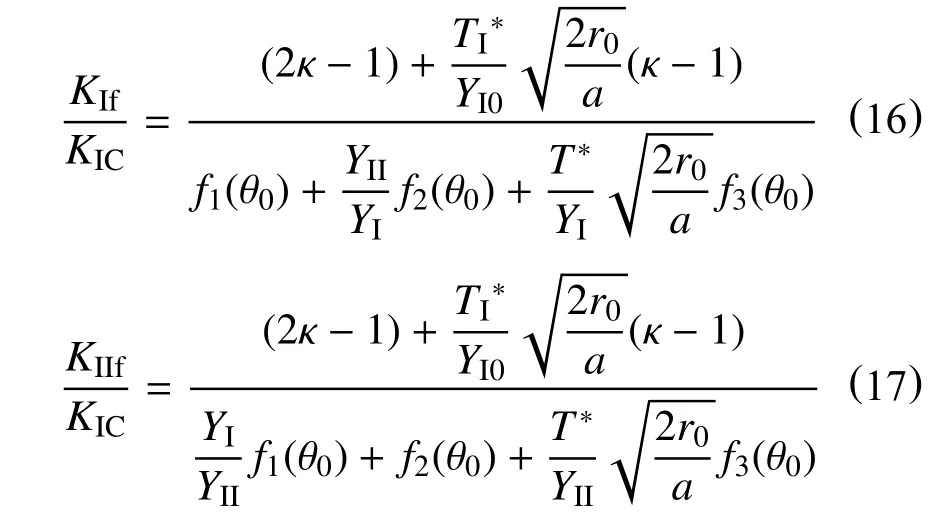
需要说明的是，这里的和YI0分别表示纯I型加载时的无量纲T应力和I 型应力强度因子。为了利用广义最大周向应变准则，我们还应知道裂纹尖端临界距离r0的大小。对于岩石等大多数脆性或准脆性材料，临界距离r0（也被叫作裂纹扩展半径）通常被认为是一个材料常数，它表示裂纹尖端断裂过程区的大小，可用式（18）进行计算[8]

KIC为纯I 型断裂韧度，σt为抗拉强度，均可由试验测得。对于一定加载条件下的中心裂纹圆盘试件，如果已知ν、YI、YII、Y*和r0等相关参数，我们就可以使用式（15）计算裂纹开裂角θ0，并利用式（16）和式（17）计算I～II 复合型断裂韧度的比值KIf/KIC和KIIf/KIC。为了进一步讨论T应力以及泊松比等参数对裂纹开裂角以及复合型断裂韧度的影响规律，我们仅以相对裂纹长度为0.5 的中心裂纹圆盘试件为例来加以说明。

图4 给出了平面应力状态下泊松比ν=0.25，α取不同值时基于广义最大周向应变准则的开裂角和断裂韧度比值。

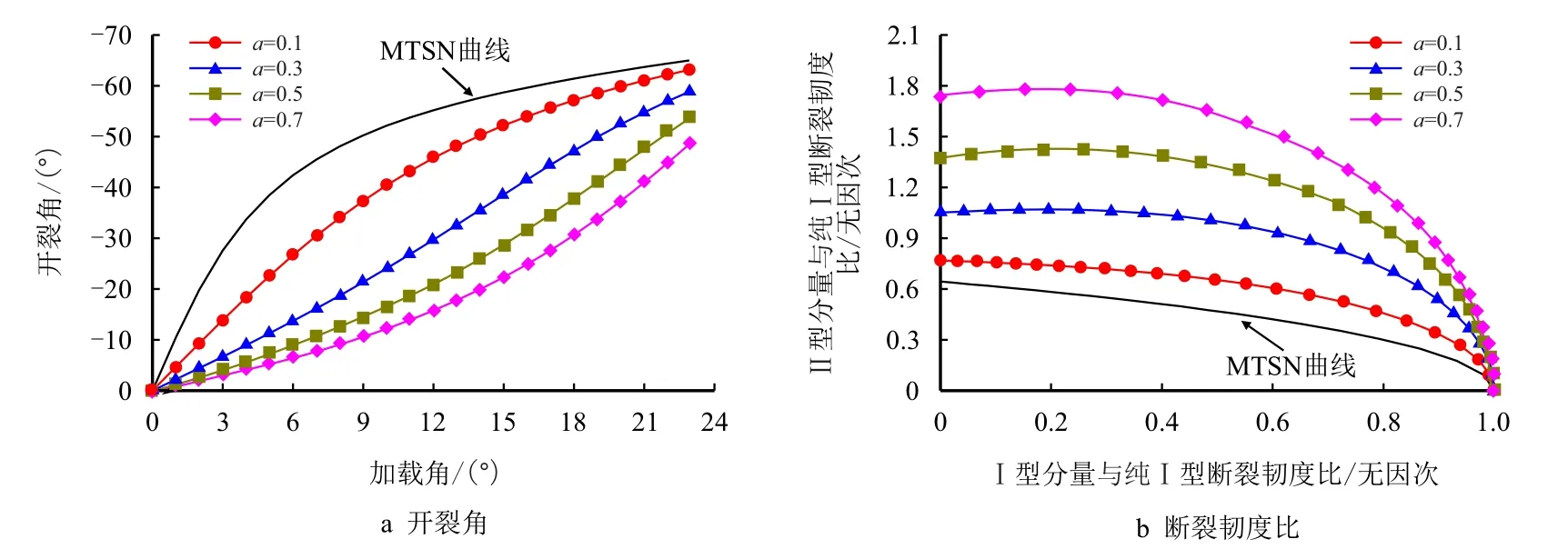
图4 不同α 时基于GMTSN 准则的开裂角和断裂韧度比值Fig.4 Predictions based on the GMTSN criterion for fracture initiation angle and fracture toughness ratio for different values of α

从图中可以看出，与传统的最大周向应变准则相比，由于拉-剪状态下中心裂纹圆盘试件裂纹尖端的T应力均为负值。负T应力的存在会使得裂纹开裂角θ0的绝对值减小。

从图4 中还可以看出，裂纹尖端的临界距离r0对基于广义最大周向应变准则的开裂角以及断裂韧度比值都有较大的影响。

开裂角θ0的绝对值总是随着临界距离r0的增大而减小，而II 型分量与纯I 型断裂韧度的比值则是随着临界距离r0的增大而增大。可见，裂纹尖端的T应力和临界距离r0对中心裂纹圆盘试件的扩展路径以及断裂韧度均有较大的影响。这与基于广义最大周向应力准则[5]以及广义最小应变能密度因子准则[15]的结论完全一致。

图5a 和图5b 分别显示了平面应力状态下，不同泊松比ν 时，基于广义最大周向应变准则的开裂角和断裂韧度比值。

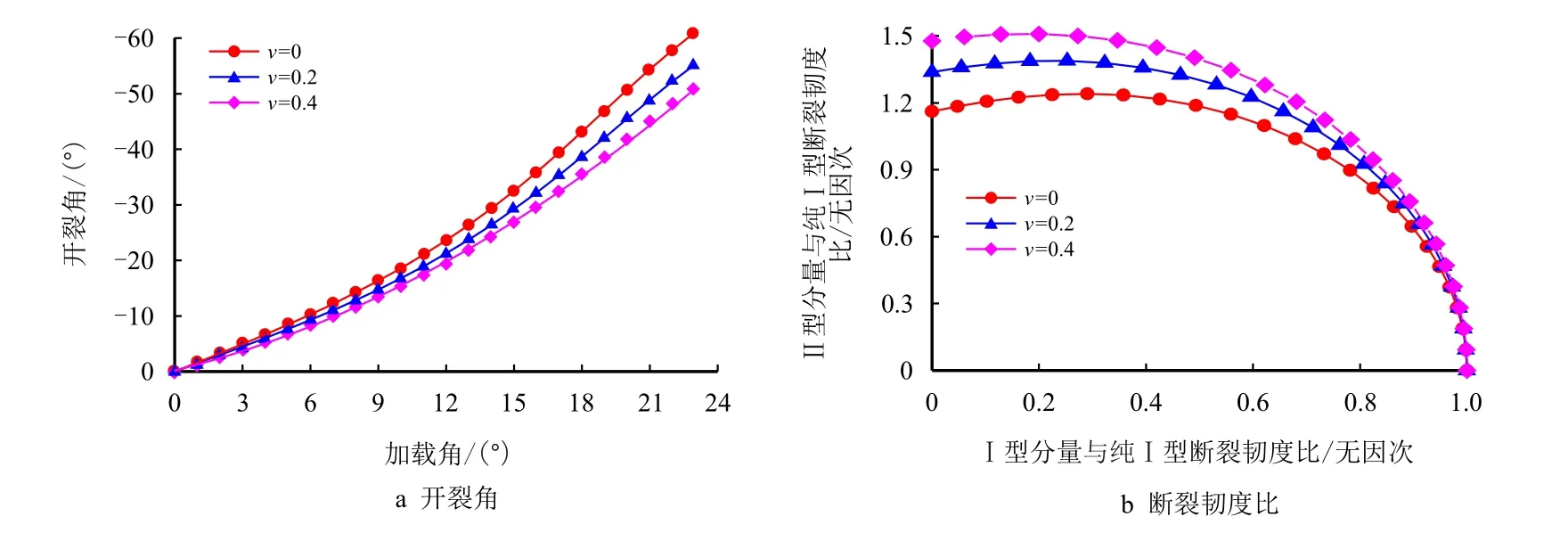
图5 不同泊松比ν 时基于广义最大周向应变准则的开裂角和断裂韧度比值Fig.5 Predictions based on the GMTSN criterion for fracture initiation angle and fracture toughness ratio for different Poisson’s ratio ν

从图中可以看出，基于广义最大周向应变准则的开裂角的绝对值总是随着泊松比ν 的增大而减小；然而，II 型分量与纯I 型断裂韧度的比值却是随着泊松比ν 的增大而增大。

由此可见，泊松比ν 对中心裂纹圆盘试件的裂纹扩展路径和断裂韧度比值也有较大的影响。值得注意的是，如果忽略了泊松比ν 的影响（即ν=0），则广义最大周向应变准则将退化为广义最大周向应力准则[22-23]。

3 基于中心裂纹圆盘试件的砂岩复合型断裂试验

为了进一步验证广义最大周向应变准则的可靠性，我们利用中心裂纹圆盘试件开展了一系列的I～II 复合型断裂试验。试验选用均质性较好的砂岩作为研究对象，为了尽量避免因岩样的个体差异所引起的试验误差，所有试件均取自同一块颗粒细致紧密，均匀性较好的青砂岩试样。试验测得这种青砂岩的干密度为2.24 g/cm3，含水率为1.20%，泊松比为0.21，抗拉强度为2.67 MPa。通过XRD 分析表明，其矿物成分主要包括石英，斜绿泥石，钠长石和基性磷铝石[27]。此次试验使用的中心裂纹圆盘试件的直径D=75.0 mm，厚度t=25.0 mm，相对裂纹长度a/R=0.5，槽宽约为0.8 mm。中心裂纹圆盘试件的加工过程可以参考文献[28]，加工过程中对所有试件进行筛选，剔除差异性较大的试样。

此次试验共设计了16 个试件，分为4 组，加载角分别为0°、10°、15°和23°，分别测量砂岩的纯I型、纯II 型以及复合型断裂韧度。试验在四川大学破坏力学与工程防灾减灾四川省重点实验室进行，采用电子万能材料试验机进行加载。

试验加载方式采用位移加载控制，前人试验表明[29]，当位移加载速率在0.005～0.1 mm/min 变化时，加载速率对岩石断裂韧度的影响可以忽略不计。此外，很多学者采用位移加载速率为0.05 或0.08 mm/min 来进行准静态断裂试验[8，28-29]。

因此，我们最终选取位移加载速率为0.05 mm/min。对于每个试件，均加载至裂纹扩展破坏，记录下完整的载荷-位移曲线，并注意观察试件的破裂过程，典型砂岩试样的破坏形态如图6 所示。从图6 中可以看出，对于纯I 型加载时，裂纹总是沿着预制裂纹方向进行扩展；而I～II 复合型加载（包括纯II 型）时，裂纹总是偏离预制裂纹的方向扩展，从裂纹尖端扩展至上下压头处，与预制裂纹方向形成一定的夹角。

图6 典型砂岩破坏形态图Fig.6 Fracture modes of typical sandstone

将试验测得的最大荷载代入中心裂纹圆盘试件的应力强度因子公式即可计算出不同加载条件下砂岩的临界应力强度因子即断裂韧度值，试验测试结果见表1 所示。

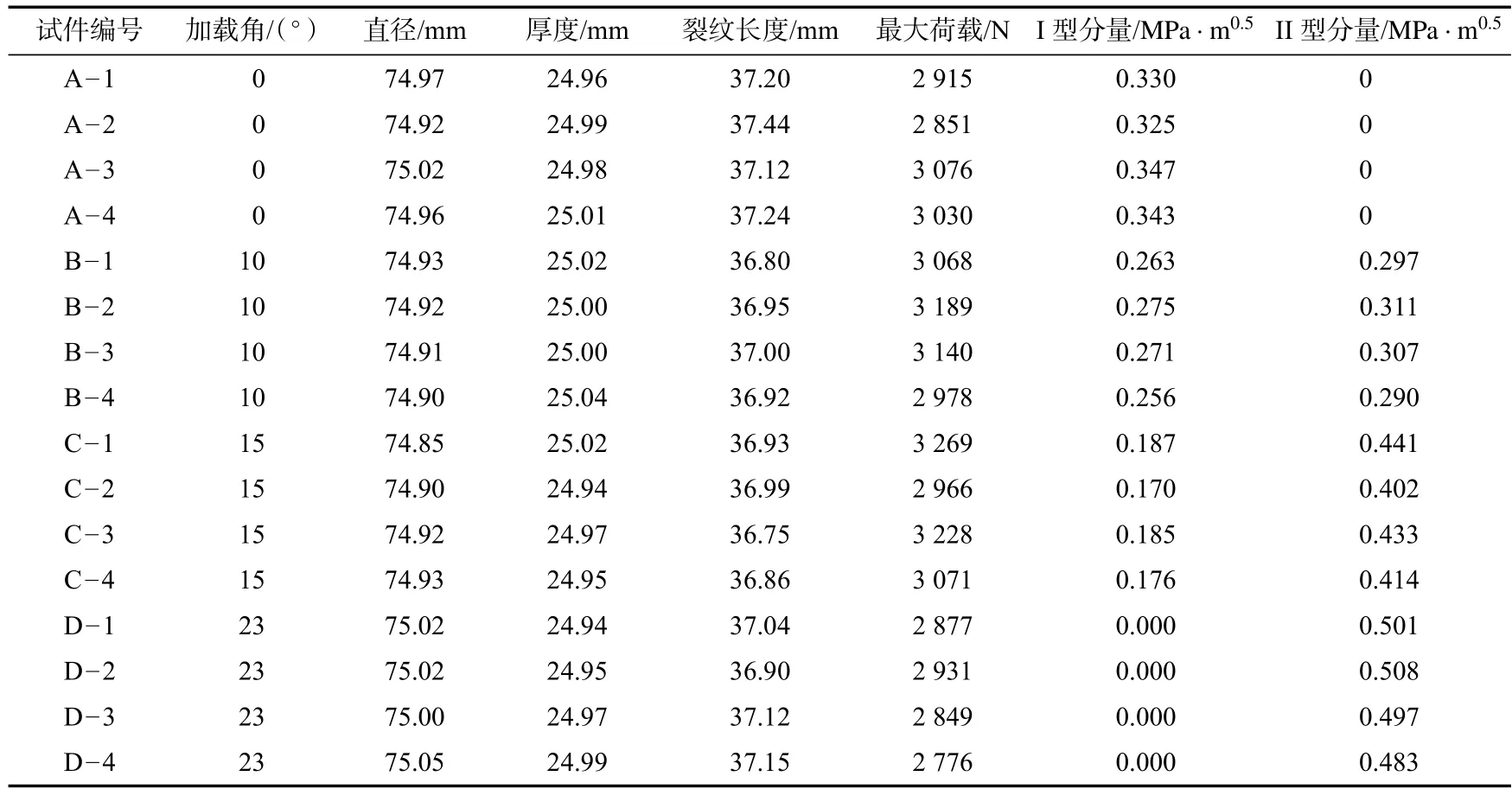
表1 砂岩I～II 复合型断裂韧度试验结果Tab.1 Test results of mixed mode I-II fracture toughness for sandstone

从表1 可以看出，砂岩断裂韧度试验结果的离散性较小，试验结果较为可靠。试验测得此种砂岩的纯I 型、纯II 型断裂韧度分别为0.337 和0.497 MPa·m0.5，纯II 型断裂韧度与纯I 型断裂韧度的比值为1.48。当加载角为10°时，砂岩的I 型和II 型断裂韧度分量分别为0.266 和0.301 MPa·m0.5；而加载角为15°时，I 型和II 型断裂韧度分量分别为0.180 和0.423 MPa·m0.5。可见，I 型断裂韧度分量随着加载角的增大而减小，而II 型断裂韧度分量随着加载角的增加而增大。

4 广义最大周向应变准则的试验验证

为了利用广义最大周向应变准则对本文断裂试验结果进行评估，进一步验证该准则的有效性，图7给出了基于中心裂纹圆盘试件测得的砂岩断裂韧度比值的关系曲线图。

同时，基于广义最大周向应变准则和广义最大周向应力准则的理论值也一并作于图7 中。从图7中可以看出，基于传统的最大周向应变准则和最大周向应力准则的理论预测值总是远小于试验值，这主要是因为传统的最大周向应变准则和最大周向应力准则都只考虑了裂纹尖端的奇异项（应力强度因子），但却忽略了裂纹尖端非奇异项（如T应力）的影响。

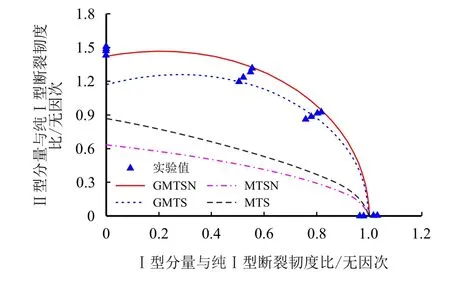
图7 砂岩复合型断裂韧度理论预测值与试验值的对比Fig.7 Comparison of theoretical values based on fracture criteria for mixed mode fracture resistance of sandstone with the test result

考虑了T应力的广义最大周向应变准则和广义最大周向应力准则能对试验结果进行很好的预测。例如，当加载角为15°时，试验测得的断裂韧度比值KIf/KIC和KIIf/KIC分别为0.534 和1.255。

根据广义最大周向应变准则，I～II 复合型断裂韧度比值KIf/KIC和KIIf/KIC的理论值分别为0.552，1.328；而基于广义最大周向应力准则的断裂韧度KIf/KIC和KIIf/KIC比值分别为0.500，1.205。

特别是纯II 型时，根据广义最大周向应变准则，断裂韧度比值KIIC/KIC的理论预测值为1.42，与断裂韧度比值的试验值1.48 非常接近，试验测试值与理论预测值之间的相对误差仅为4.1%。

然而，基于广义最大周向应力准则，则断裂韧度比值KIIC/KIC的理论预测值约为1.18，比试验值小20.3%。由此可见，纯II 型时，考虑了T应力影响的广义最大周向应变准则比广义最大周向应力准则更为准确。

侯成等[6]为了研究混凝土的I～II 复合型断裂特性，利用内径为70 mm，高30 mm 的钢模制作了四种不同配合比的混凝土中心裂纹圆盘试件。这些混凝土试件主要包括：砂浆试件（M），小骨料混凝土试件（SC），大骨料低强度混凝土试件（LC）和大骨料高强度混凝土试件（HC），其力学性能参数如表2所示。

浇筑前，他们在钢模底部中心位置安装了一块厚0.8 mm，宽14 mm 的薄钢片，浇注成型后将薄钢片取出，形成初始的中心裂纹。而后，待试件达到养护要求后，他们再利用细钢丝锯对初始裂纹进行处理，最终形成的中心裂纹长度为28 mm，相对裂纹为0.4。对于每种类型的混凝土试件，设计了6 组不同的加载角，分别测量其纯I 型、纯II 型以及I～II复合型断裂韧度。

侯成等[6]通过开展了一系列的断裂试验，测得4 种混凝土的纯I 型断裂韧度和抗拉强度，如表2 所示，根据公式（18）计算的临界距离也列于表中。

表2 混凝土材料的力学性能参数[6]Tab.2 Mechanical properties of concrete materials[6]

图8 给出了4 种混凝土材料在不同加载角作用时裂纹开裂角的试验值与基于断裂准则的理论预测值的对比图。

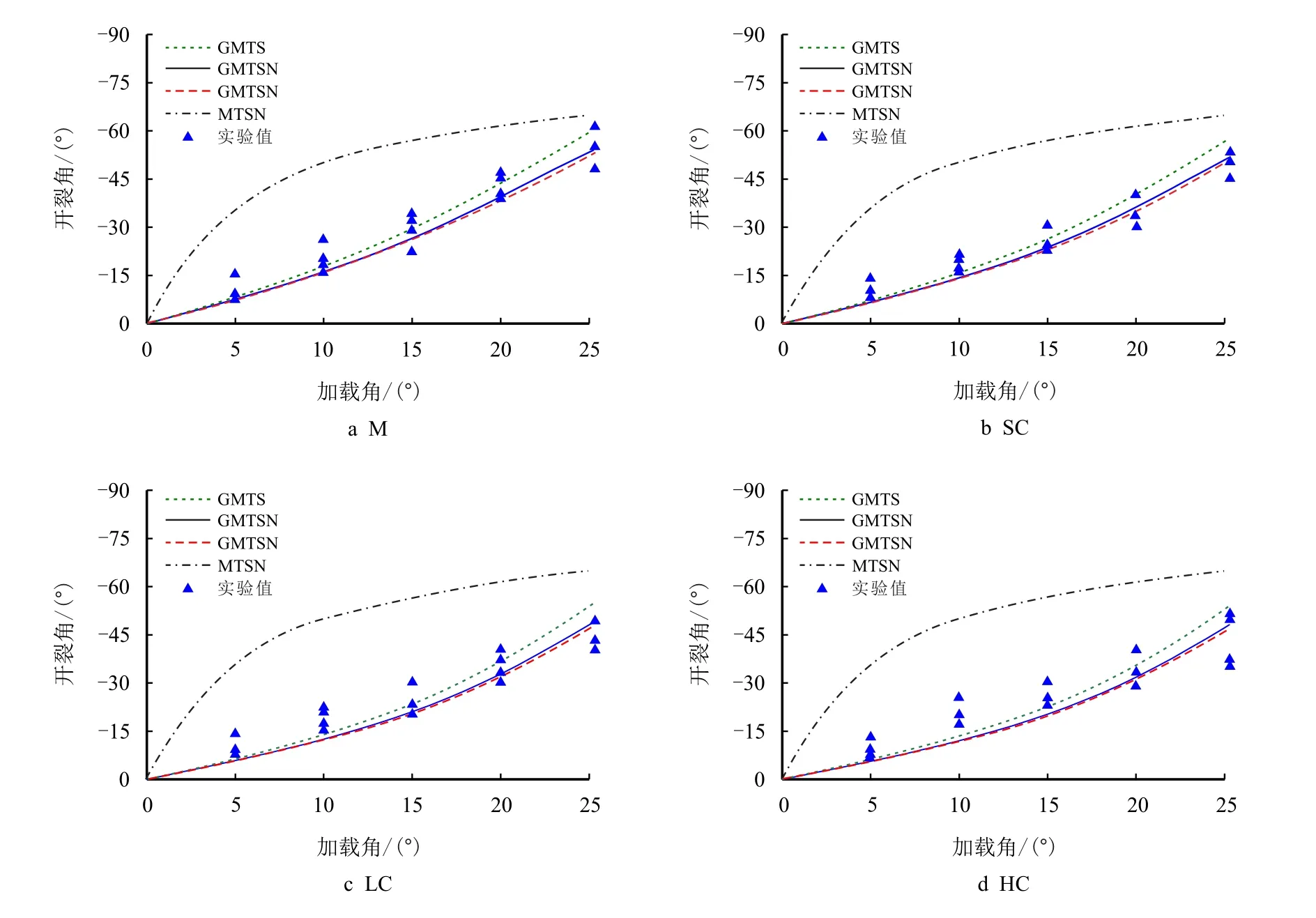
图8 混凝土开裂角理论预测值与试验值的对比[6]Fig.8 Comparison of the theoretical values based on the fracture criteria for fracture initiation angle of concrete materials with the test results[6]

从图中可以看出，基于传统的最大周向应变准则，其理论预测值与试验值之间存在较大的偏差，主要是因为该准则未考虑裂纹尖端T应力的影响。然而，考虑了T应力影响的断裂准则都能对试验结果进行很好的预测。

此外，根据广义最大周向应变准则，在平面应力条件下得到的裂纹开裂角的绝对值要稍大于平面应变条件下得到的开裂角。

两种平面条件下基于广义最大周向应变准则的开裂角的绝对值总是小于基于广义最大周向应力准则的开裂角。

图9 给出了4 种混凝土材料I～II 复合型断裂韧度的试验值与基于断裂准则的理论值的对比图。

从图9 可以看出，基于考虑了T应力影响的广义最大周向应变准则和广义最大周向应力准则的理论预测值与试验测试值符合的很好。

然而，基于仅考虑了应力奇异项的最大周向应变准则的理论预测值远小于试验值，这主要是因为其忽略了裂纹尖端T应力的影响。

基于广义最大周向应变准则，平面应变条件下得到的II 型分量与纯I 型断裂韧度比值总是比基于平面应力条件下得到的值稍大，但差异并不明显。与广义最大周向应力准则相比，基于应变的广义最大周向应变准则能提供更大的断裂韧度比值。尽管，广义最大周向应力准则能对试验结果进行很好的预测，但是，在纯II 型时，基于广义最大周向应力准则的理论预测值总是小于试验值。

侯成等[6]也曾利用考虑了Williams 级数展开式中的前3 项修正的最大周向应力准则和仅考虑前2 项的广义最大周向应力准则对试验结果进行了对比，利用Williams 级数展开式中的前3 项修正的最大周向应力准则能明显提高理论预测值的精度，见表3 所示。

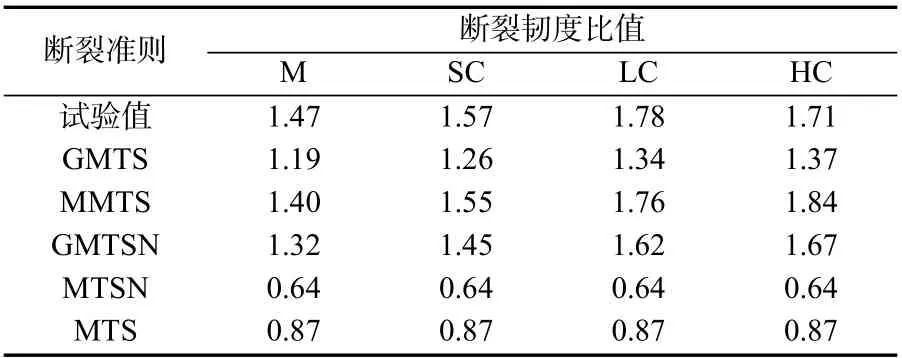
表3 基于不同断裂准则的理论值与试验值对比Tab.3 Comparison of the theoretical values based on different fracture criteria with the experimental values

然而，与广义最大周向应力准则相比，考虑前3项修正的最大周向应力准则的表达式过于复杂，另外两个系数只能通过数值方法进行计算[6]，并且其计算过程也较为繁琐，因此，该准则在实际运用时并不方便，不便于推广。尽管广义最大周向应变准则也只考虑了Williams 级数展开式中的前两项，但对于纯II 型裂纹的预测精度明显要优于广义最大周向应力准则。与广义最大周向应力准则相比，广义最大周向应变准则同时考虑了裂纹尖端的多个应力分量（σrr，σθθ，σzz）和泊松比ν 的影响；然而广义最大周向应力准则只考虑了裂纹尖端的周向应力分量。Aliha 等[30]通过三维有限元分析指出，泊松比对含裂纹构件的应力强度因子和T应力都有较大的影响。

泊松比是广义最大周向应变准则中较为重要的一个材料参数，它是区分基于应变和基于应力的断裂准则的关键参数。

5 结论

（1）根据广义最大周向应变准则，中心裂纹圆盘试件中由于负T应力的存在，会使得裂纹开裂角的绝对值减小，同时使得临界应力强度因子（断裂韧度）的值增加。

（2）开裂角的绝对值总是随着临界距离和泊松比的增大而减小；断裂韧度比值却是随着临界距离和泊松比的增加而增大。

（3）考虑了T应力影响的广义最大周向应变准则能很好的对试验结果进行预测；在纯II 型时，基于广义最大周向应变准则的理论预测值比基于广义最大周向应力准则的理论值更接近试验值。

（4）虽然广义最大周向应变准则能有效的对基于中心裂纹圆盘试件的I～II 复合型断裂试验结果进行预测，但对于其他构型试件（如：SCB，CTS，TPB等）的断裂试验结果是否也有很好的预测效果，则需做进一步的验证。

符号说明

σrr半径r方向的正应力分量，MPa；

σθθ角度θ 方向的正应力分量，MPa；

σrθ微元体的切应力分量，MPa；

KII 型应力强度因子，MPa·m0.5；

KIIII 型应力强度因子，MPa·m0.5；

r裂纹尖端在极坐标下的半径坐标，mm；

T平行于裂纹面非奇异常数项应力，MPa；

εθθθ方向的应变，无因次；

E杨氏弹性模量，MPa；

εt最大的周向应变，无因次；

σt抗拉强度，MPa；

B双轴应力比，无因次；

a半裂纹长度，mm；

r0临界半径，mm；

Keff等效应力强度因子，MPa·m0.5；

KIC纯I 型加载的断裂韧度，MPa·m0.5；

θ0裂纹开裂角，（°）；

KIfI 型断裂韧度分量，MPa·m0.5；

KIIfII 型断裂韧度分量，MPa·m0.5；

P试件所受集中荷载，kN；

R中心裂纹圆盘试件的半径，mm；

t中心裂纹圆盘试件的厚度，mm；

YII 型无量纲应力强度因子，无因次；

YIIII 型无量纲应力强度因子，无因次；

T*无量纲T应力；无因次；

纯I 型无量纲T应力，无因次；

YI0纯I 型无量纲应力强度因子，无因次。