精密指向组件控制参数自整定技术研究
王绪硕,陈青山,夏润秋
(北京信息科技大学 仪器科学与光电工程学院,北京 100192)
0 引言
精密指向组件是对光束方向进行精确控制的一种高度集成的精密光学部件,具有速度快、精度高、体积小、重量轻等特点,广泛应用于激光通信、图像精密跟踪、激光武器等领域[1-2]。目前,精密指向组件正朝着高带宽、大转角范围的方向发展。
精密指向组件是高阶系统,其控制方式主要是优化的PID控制。PID参数主要通过人工试凑的方法来实现,效率低下且难以达成最优控制[3-4]。而且精密指向组件在工作过程中受环境温度变化、周围环境振动等影响,其特性可能会发生改变,增加人工整定的难度。而自整定算法就是对PID参数进行自动整定的一种技术,可以提高参数整定效率。基于精密指向组件的自整定技术的研究具有重要的意义[5]。
目前,常用的自整定算法主要有神经网络算法、模糊控制算法、遗传算法等。继电反馈算法也是一种自整定算法,不需要系统的数学模型[6],只需要得到系统极限环振荡下的临界信息,即可整定出PID参数。Astrom等[7-8]提出继电反馈算法,Luyben等[9]通过理想继电整定与关键点的幅相关系改进了经验整定公式,但这种方法忽略了高次谐波,存在一定的误差。Yu[10]提出了一种饱和继电反馈实验的方法,减小了因只考虑一次谐波而产生的误差。此外,还有带滞环的继电反馈控制克服测量噪声的影响,带附加环节的继电反馈控制使得其应用范围更加广泛等。
继电反馈自整定技术研究虽然发展迅速,但多为基于理论的研究或进行仿真的分析,很少应用于实际的控制系统[11]。在实际的控制过程中,由于对控制系统的要求不同,需要对整定公式进行调整,这是很多研究没有关注的[12]。
本文提出了一种改进型继电反馈自整定算法,附加积分环节,并对整定公式进行改进。以精密指向组件为研究对象,自动整定出PID参数,实现精密指向组件的优化控制。
1 精密指向组件基本构成和系统模型
精密指向组件由执行机构、支撑机构、反馈部件等组成[13]。精密指向组件有压电陶瓷驱动和音圈电机驱动两大类,本文采用音圈电机作为执行机构。音圈电机是一种特殊形式的直流驱动电机,具有结构简单、体积小、响应速度快等特性。音圈电机结构如图1所示。
若要对精密指向组件的控制参数自整定进行研究,首先需要建立其精确的数学模型,推导出传递函数。线圈回路的动态电压平衡方程式为
(1)
式中:U为音圈电机线圈两端电压;E为电动势;L为线圈在磁场中的长度;I为线圈上电流大小;R为线圈电阻,L为电感。建立音圈电机的动力学模型:
G1(x)=
(2)
式中:Km为电机力矩系数;Ke为电机反电动势系数;mc为音圈电机动子质量;c为等效阻尼系数;k为弹性系数。
精密指向组件模型如图2所示,其力矩平衡方程式为
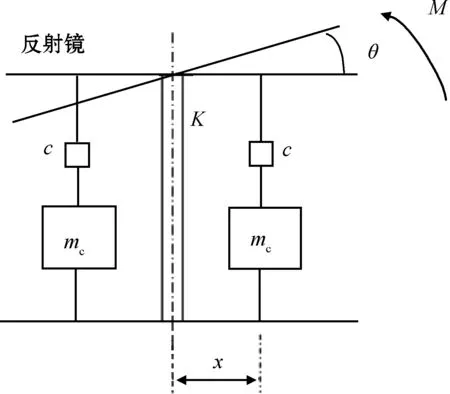
图2 精密指向组件结构模型
(3)
式中:M为力矩;J为反射镜转动惯量;θ为偏转角度;K为柔性支承轴向扭转刚度;x为力作用点到转轴的距离。
由此可得精密指向组件偏转角度与控制力矩之间的传递函数为
(4)
其中:
由式(2)、(4)可得精密指向组件开环传递函数为
G(s)=
(5)
其闭环传递函数为
Φ(s)=
(6)
由其传递函数可知,精密指向组件是一个三阶系统。实际用到的精密指向组件实物如图3所示。其闭环带宽为300 Hz,转角范围为±2 000″,分辨率为1 μrad,口径为76 mm,负载为55 g,其传递函数为

图3 精密指向组件实物
G(s)=
(7)
2 控制参数自整定
2.1 传统继电反馈自整定
传统的继电反馈自整定算法结构如图4所示,其包含调节模式和整定模式两个过程,在整定模式下,给定一个目标值和继电器幅值d,闭环系统在继电器的非线性环节作用下做周期振荡运动,根据其振荡曲线求出系统的临界信息Ku、Tu,再根据整定公式,整定出系统的PID参数。然后,开关切换到调节模式,将整定出的PID参数写入PID控制器,实现PID控制。
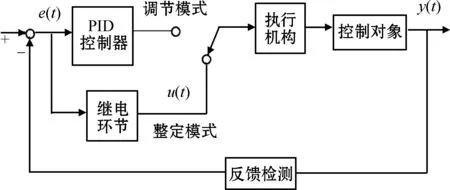
图4 传统继电反馈自整定示意
2.2 改进型继电反馈自整定
传统的继电反馈自整定技术适用于被控对象在高频处具有至少-π的相位滞后的系统,对于一些高阶系统则不适用,而精密指向组件就是一种典型的高阶系统。为了扩大继电反馈自整定算法的适用范围,在被控对象的前面串联一个积分环节1/s,如图5所示。
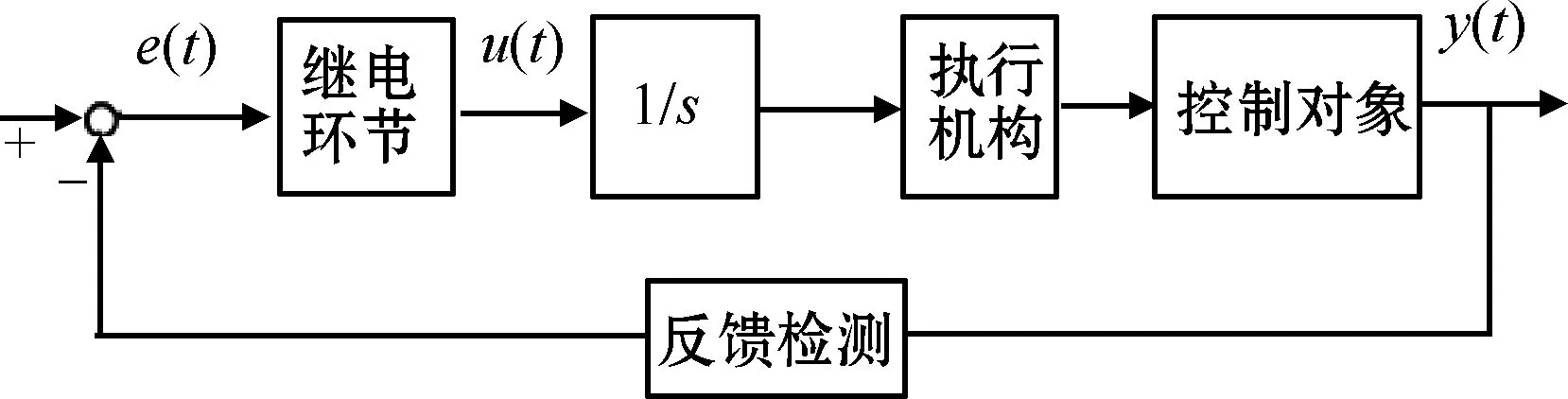
图5 改进型继电反馈自整定示意
改进后,相当于将被控对象人为地滞后一定的时间,被控对象只需要具有至少-π/2的相位滞后,就可以产生极限环振荡[14]。
继电反馈自整定的关键在于要使系统产生极限环振荡,用描述函数法来确定系统的临界增益Ku以及临界周期Tu。根据继电特性,其描述函数为
(8)
式中:ε为滞环宽度;a为振荡幅值;d为继电输出的幅值。当ε=0时,式(8)可以简化为
(9)
设振荡能源为w0,
(10)
由于理想继电的描述函数与实轴负实部重合,所以:
(11)
整定过程中,被控系统的运动曲线如图6所示,其中
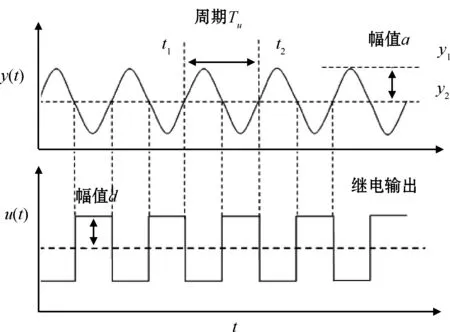
图6 被控系统运动曲线
a=y1-y2,Tu=t2-t1
(12)
PID参数决定着系统的稳定性,PID作用过程Nyquist图如图7所示,图7中Im指复数的虚部,Re指实部。P值可以使系统Nyquist图上的一点A沿着曲线径向移动,I和D值使得A点垂直于径向移动。最终使A点移动到同时满足幅值裕度和相位裕度的位置。
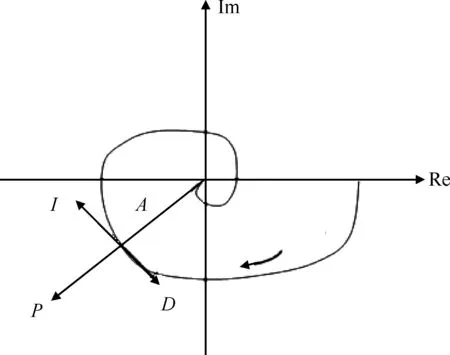
图7 PID作用过程Nyquist图
设控制器的结构形式为:
(13)
(14)
(15)
则有下列关系:
Kp=KusinΦm/Am,Ti=αTd
(16)
Astrom和Haggland推荐的幅值裕度为2~5,相角裕度为30~60°,α一般取4。
控制参数自动整定流程如图8所示。在上位机整定工具包中选择整定模式,设定反射镜偏转角度和继电幅值。点击自整定按钮,上位机可以计算出PID参数并将其写入控制器中。切换到调节模式,即可实现PID控制。若控制效果不理想,则可切换到整定模式重新整定。
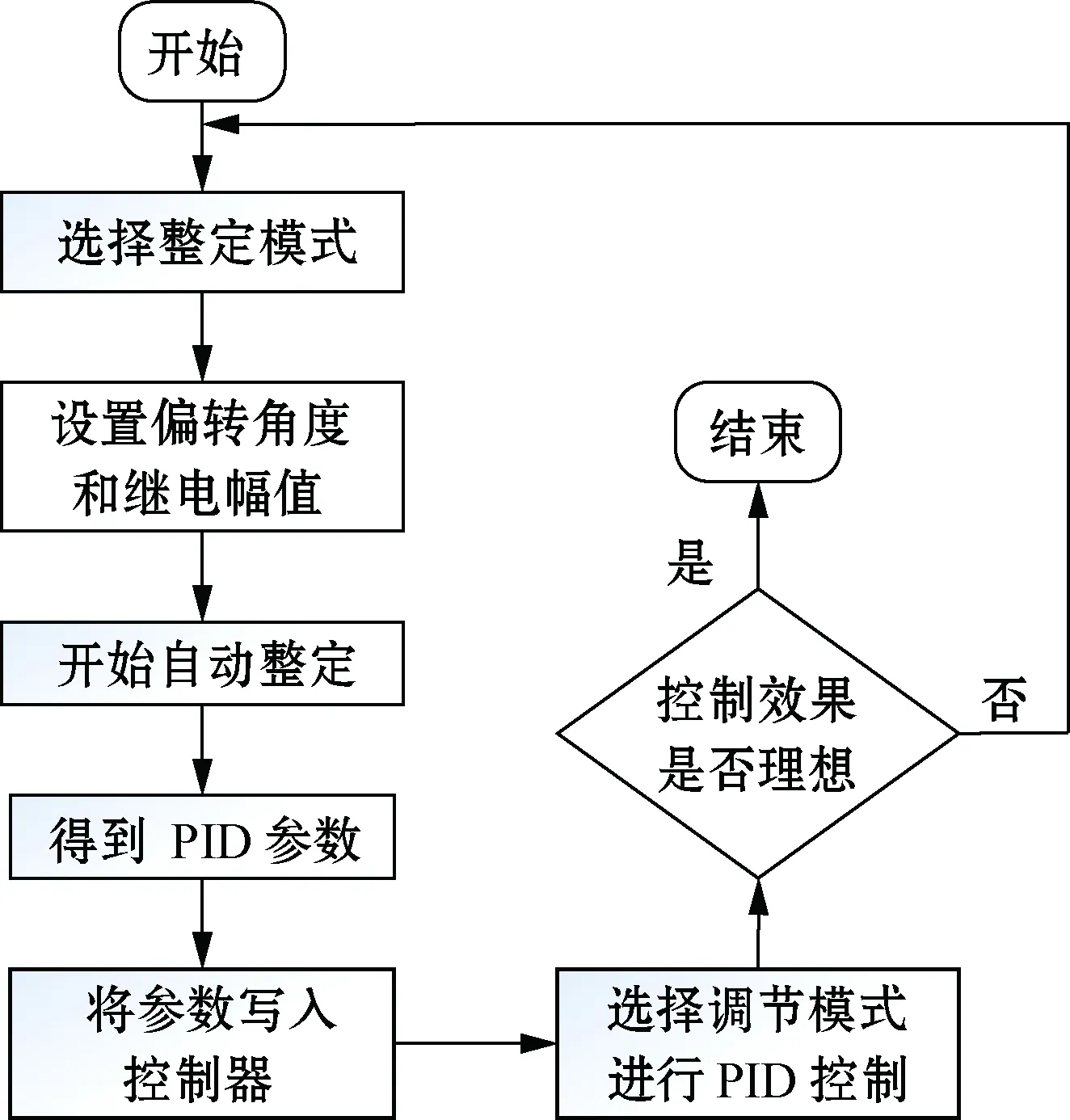
图8 自整定流程
3 可行性验证
为了验证自整定算法的可行性,采用Matlab软件,建立精密指向组件的数学模型,并搭建改进型继电反馈自整定算法。目标θ值随机取10″,继电输出d=4 V,系统产生可以极限环振荡,振荡曲线如图9所示。
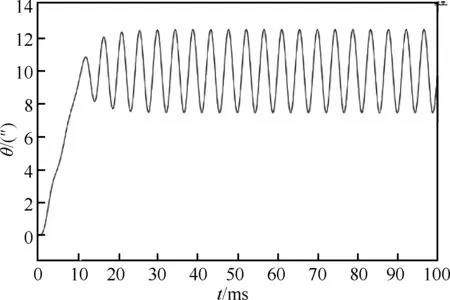
图9 极限振荡曲线
根据Matlab储存的系统振荡曲线(图9)的数据,求出a=2.550,Tu=4.463 s,则Ku=1.997。幅值裕度Am取3.5,相位裕度Φm取45°,α=4,则根据式(16)可以得到的PID参数为:Kp=0.399,Ti=0.589,Td=0.147。为了适应精密指向组件高带宽、低超调量的要求,对式(16)进行改进,提高比例和积分系数提高速度,增大微分系数减少超调,改进后的PID参数与临界信息的关系如表1所示。由此可以得到改进后的PID参数为:Kp=0.679,Ti=1.589,Td=0.544。将得到的PID参数写入控制器中,得到平滑的阶跃响应曲线如图10和图11所示。

表1 改进型PID参数与临界信息的关系
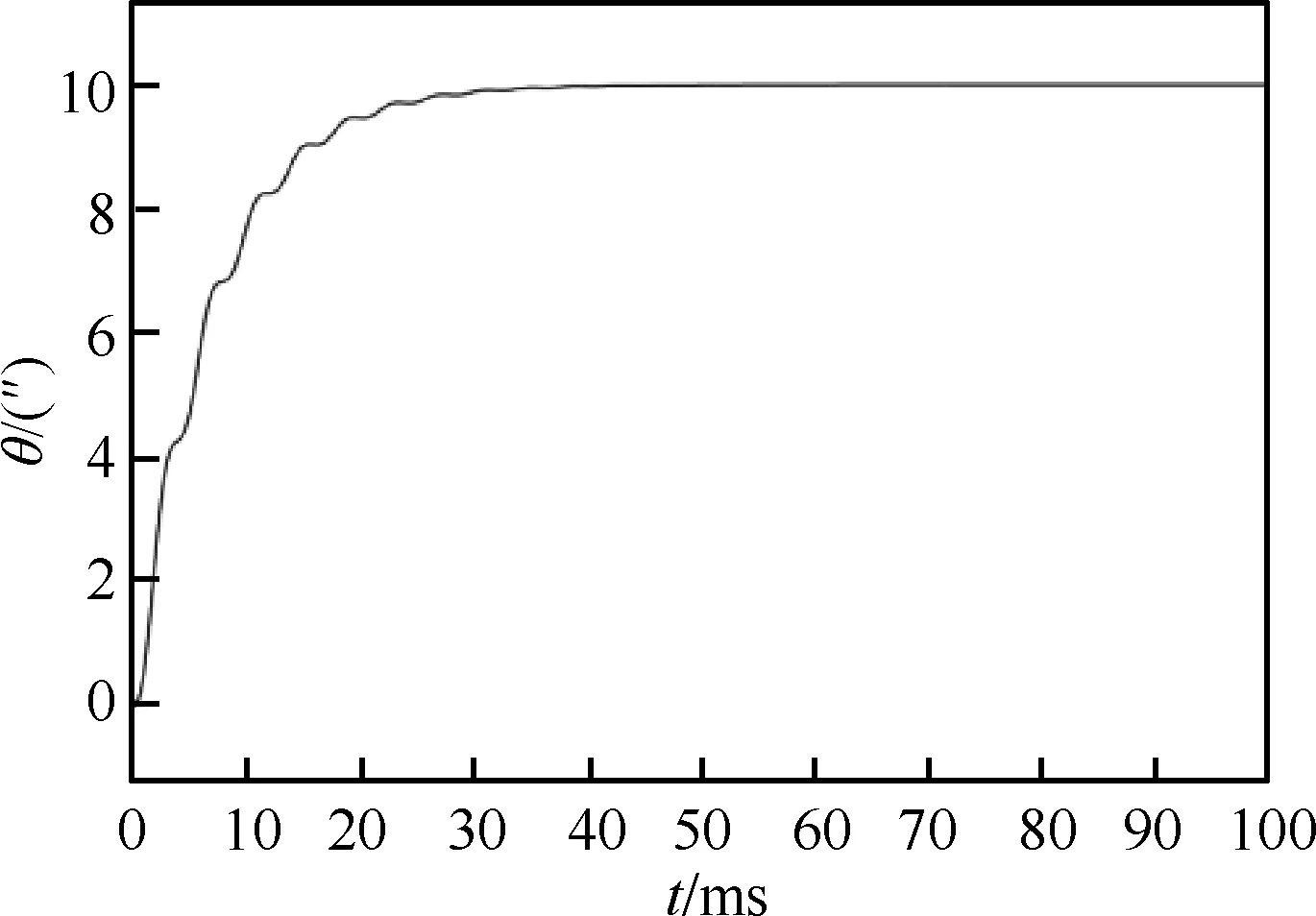
图10 原始公式阶跃响应曲线
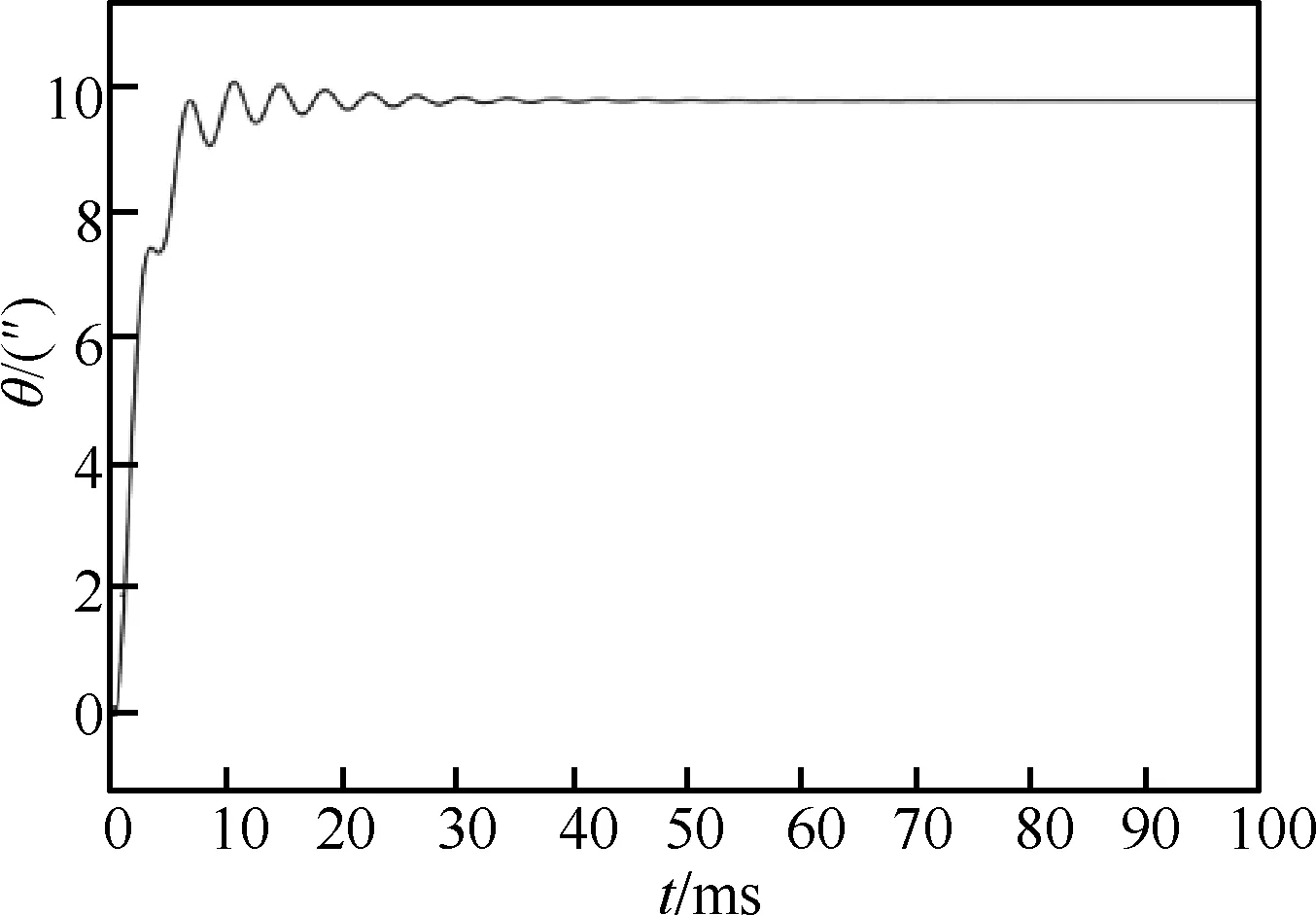
图11 改进公式阶跃响应曲线
从图中可以看出,改进的继电反馈自整定算法应用在三阶系统中,可以使系统产生极限环振荡,验证了该算法的可行性,且上升时间相较原始整定方法得到的结果,减少了30 ms。
4 整定过程及实验结果
为了对自整定算法的准确性进行验证,搭建实际的测试系统,如图12所示。

图12 测试系统
设计上位机整定工具包,建立精密指向组件控制板与上位机之间的串行通信。电涡流传感器将反射镜的位置信息反馈给控制板,控制板通过串口将该位置信息传递给上位机。
上位机中,设定反射镜偏转角度为100″,继电环节输出幅值为6 V。点击自整定按钮,上位机可以自动计算出PID参数并将其写入控制器中。切换到调节模式,即可实现PID控制。
实验得到的反射镜振荡曲线如图13所示。
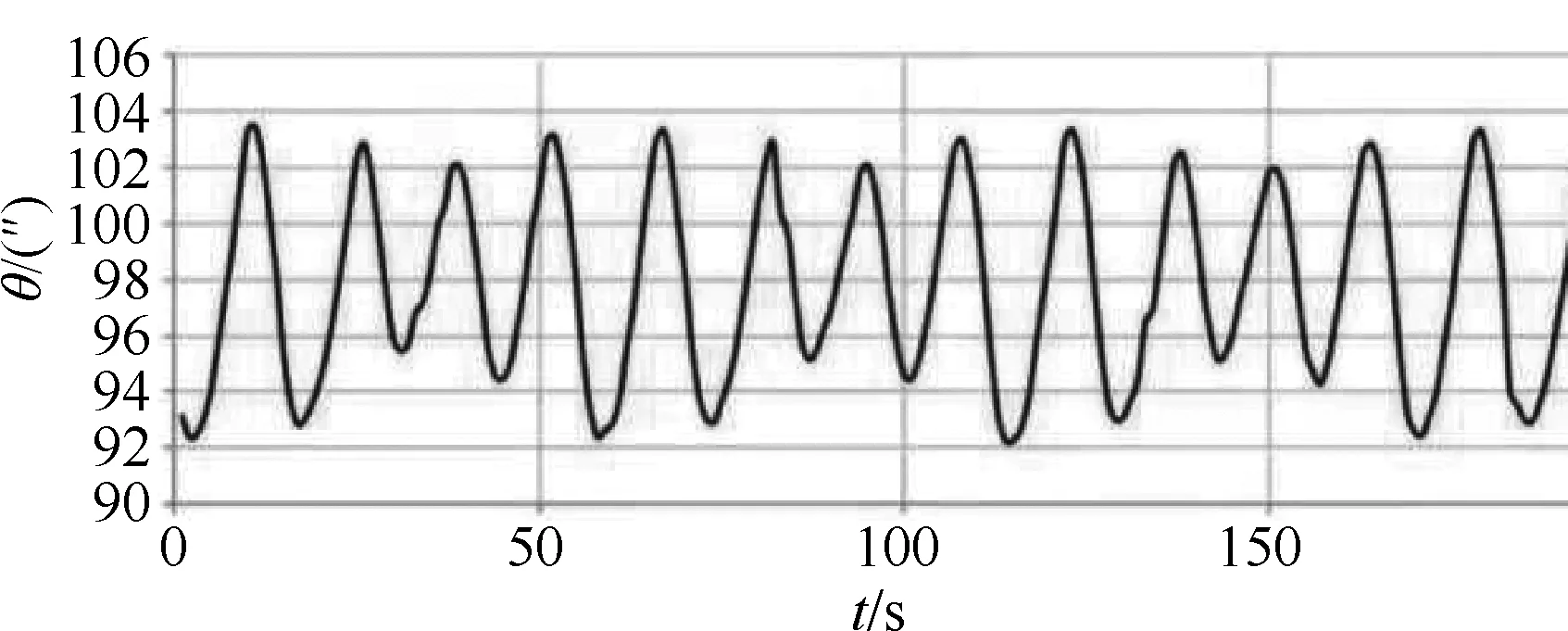
图13 反射镜振荡曲线
上位机软件显示的振荡曲线得出幅值a=4.12,计算临界增益Ku=1.855,临界周期Tu=0.008 3 s,在上位机软件中,根据表1整定规则,计算出PID参数如表2所示。
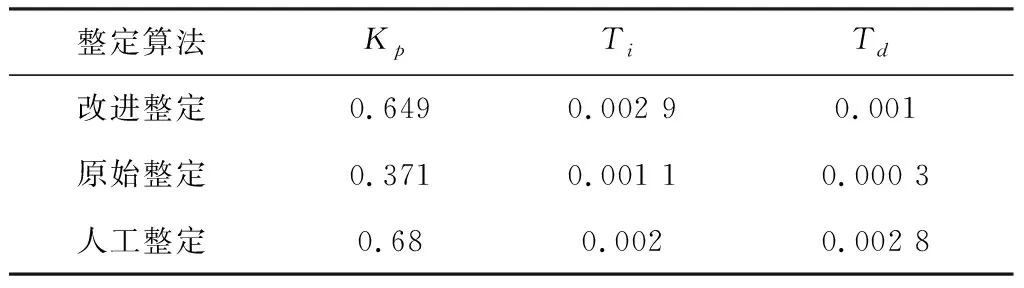
表2 三种整定方法PID参数
将PID参数写入控制器中,得到改进型算法阶跃曲线、原始整定阶跃曲线、人工整定阶跃曲线如图14所示。
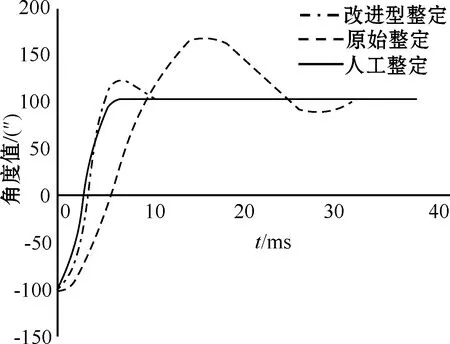
图14 三种方法阶跃响应曲线对比
对3种方法所得阶跃响应曲线的上升时间、稳定时间、超调量等数据进行对比,如表3所示。
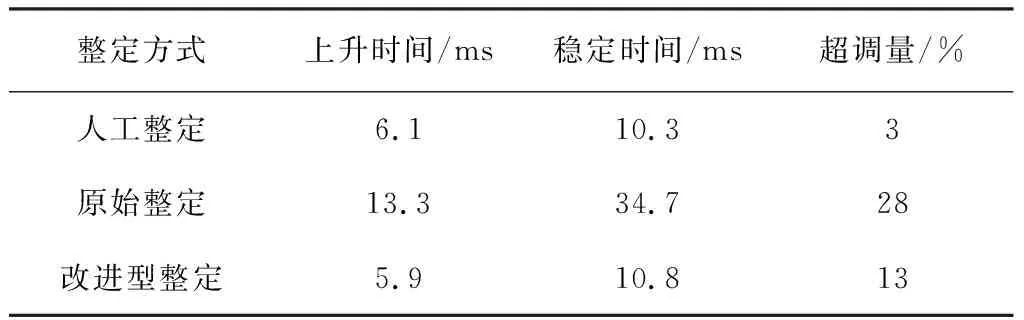
表3 三种整定方法数据对比
由表4可以看出,人工整定得到的阶跃响应曲线超调量小,上升时间和稳定时间都较短,但是整定过程花费了较多时间,效率低下,难以适应大批量生产。原始整定的结果超调量较大,上升时间和稳定时间都较长,难以满足精密指向组件高带宽的要求。而本文设计的上位机整定工具包可以自动整定出PID参数并将其写入控制器中,得到的阶跃响应曲线上升时间明显减小,且超调量更小,曲线更平稳。
上述实验是在光学平台上进行的,工作环境稳定。为了对改进型继电反馈自整定算法的抗干扰和自适应能力进行验证,在振动平台上模拟高速公路振动环境,如图15所示。

图15 振动环境测试
实验后,得到正常环境与振动环境下阶跃响应曲线如图16所示。
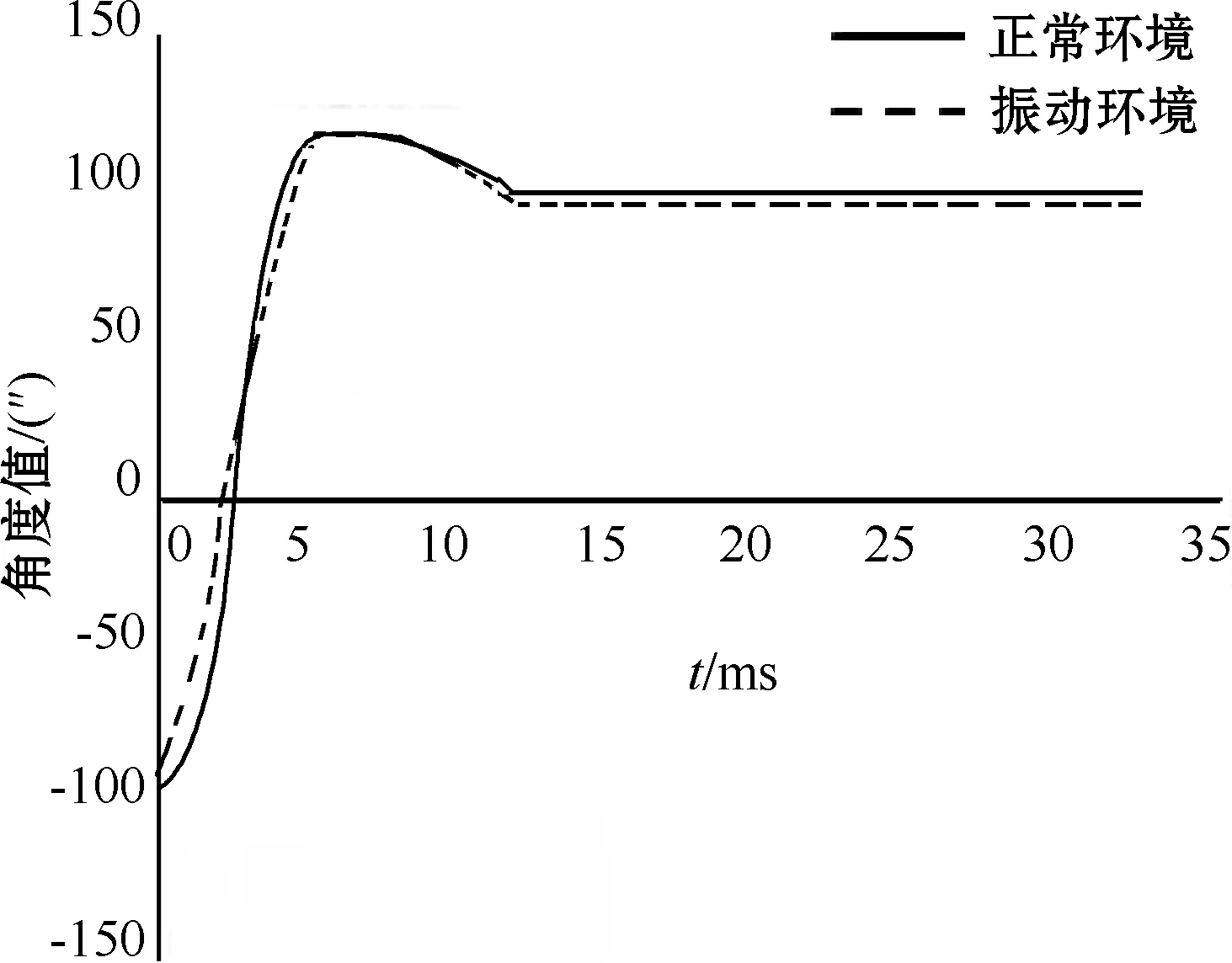
图16 两种环境下阶跃曲线
振动环境下,阶跃响应曲线超调量为10%,上升时间为5.1 ms;正常环境下,阶跃响应曲线超调量为9%,上升时间为4.9 ms。两组数据实验结果极其接近,表明改进型继电反馈自整定算法具有较强的抗干扰能力。
5 结束语
针对精密指向组件,依据继电反馈理论,对自整定算法进行研究,并对整定公式进行改进。推导精密指向组件传递函数,建立改进型继电反馈自整定算法的模型并搭建实际的精密指向组件系统。设计上位机整定工具包进行实验,结果表明:与原始的整定算法相比,改进型自整定算法超调量更小,响应速度更快。

