一种自适应混合滤波铁塔姿态解算方法

岑海伦，熊 鸣，王丽婕，李广元

(1.北京信息科技大学 自动化学院，北京 100192；2.北京信息科技大学 高动态导航技术北京市重点实验室，北京 100192)

0 引言

受酸雨、台风、地震等恶劣环境的影响，输电铁塔结构会出现不同程度的形变问题[1]，为了保障电力系统安全稳定运行，需要对铁塔形变进行监测。目前主要有3种监测方式：①基于机器视觉方法，通过卷积神经网络(convolutional neural networks，CNN)算法[2]对无人机航拍到的铁塔图像进行钢架主轴信息提取，并依据地面法线方向与轴之间的夹角来判断铁塔形变情况。这种方法属于事后检测，无法实时监测铁塔状态也不能及时预警。②基于全球导航定位系统[3-4](global navigation satellite system，GNSS)技术，在输电铁塔主要节点上装设接收机，根据节点三维坐标的变化计算出钢材的形变。然而在强电磁场或者非视距的环境中，接收机常常会出现信号丢失情况，这使得GNSS解算出来的信号不可靠。③基于惯性导航系统[5](inertial navigation system，INS)技术，由惯性传感器通过导航姿态解算方法解算当前时刻偏离初始时刻的角度，可判断铁塔当前形变情况。这种惯性传感元件几乎不受外界电磁环境干扰，具有很强的抗干扰能力[6]。

近年来，众多学者围绕导航姿态算法展开了大量的研究，涉及的姿态解算方法有高斯牛顿算法、互补滤波算法、卡尔曼滤波算法及其扩展形式。于中亚[7]提出了一种加速度反馈修正的高斯牛顿算法，将其应用于铁塔形变监测。杨金显等[8]提出了一种杆塔倾斜状态监测方法，在滤波前先将传感器采集到的数据进行降噪处理，然后由四元数解算出当前时刻倾斜角度。陈光武等[9]将非重力加速度作为信赖指标调整互补滤波控制器参数，但存在所有的姿态角共用一个控制参数的问题，并且该算法在高动态环境中滤波效果不理想。以上方法只是针对加速度计或陀螺仪进行补偿，并且动态性能和静态性能难以同时保证。陈仕毅等[10]提出了一种简化卡尔曼滤波模型，其解算精度优于传统互补滤波算法。王见等[11]通过扩展卡尔曼滤波矫正互补滤波解算的姿态角，从而抑制了数据波动。但是无论卡尔曼滤波还是扩展卡尔曼滤波算法对系统模型要求都比较苛刻，且鲁棒性较差。Sage-Husa自适应卡尔曼作为极大后验估计，可对量测噪声实时估计[12]，但存在计算量大、应对突变情况的能力较差等问题。

针对以上问题，本文提出一种基于自适应互补滤波与强跟踪卡尔曼滤波(strong tracking Kalman filter，STK)的混合算法。设计自适应互补滤波器融合陀螺仪和加速度信息，由加速度与重力向量之间的偏差修正载体角速度，再将滤波后角速度作为强跟踪卡尔曼滤波的输入矩阵。这种强跟踪滤波器无需对噪声进行实时估计，而是由比例因子直接调整当前量测噪声，不仅大大简化了计算量，而且还避免了在Sage-Husa自适应卡尔曼滤波算法中因量测噪声方差矩阵Rk非正定而导致的滤波发散问题。

1 惯性导航姿态解算

常用的姿态角解算方法包括欧拉角法和四元数法，其中四元数法因其具有计算量小、全姿态解算等优点得到了广泛的应用。为描述铁塔姿态变化，需定义两个坐标系：以地理坐标系(n系)作为姿态解算导航坐标系(R系)；以铁塔固联的坐标系作为载体坐标系(b系)，其中将载体坐标系xb轴定义为铁塔横轴方向，yb轴定义为铁塔纵轴方向，zb轴定义为铁塔竖轴方向。导航坐标系和载体坐标系之间的转换关系为

(1)

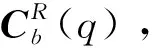
(2)

由式(2)可分别得到横滚角γ和俯仰角θ：

(3)

2 传统互补滤波理论

陀螺仪测量载体三轴角速度，经积分可求解载体三轴角度信息；加速度计测量载体三轴加速度信息。两种传感器在解算过程中各有优缺点，其中陀螺仪高频特性好，但在姿态解算过程中存在随时间递增的积分误差，因此不适合长时间单独工作[13]。加速度传感器静态不存在累计误差，但在动态环境中无法跟踪姿态变化。根据两种测量元件在频域特性上呈现的互补关系，利用互补滤波融合两种传感器的数据，其具体步骤如下：

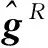
(4)

2)对加速度计输出值进行归一化：

(5)

3)载体加速度与重力矢量之间的误差向量为

(6)

4)误差向量e经PI控制器输出，可得到陀螺仪角速度的修正值δω，修正后的陀螺仪角速度为ω′=ω+δω，利用修正后的角速度参与四元数更新：

(7)

(8)

式中，Ts为采样周期

5)将更新后的四元数代入式(3)可求解出横滚角和俯仰角。

3 混合滤波算法

由于自然风具有随机性、突发性等特点，铁塔振动姿态与风速和脉振频率息息相关。面对复杂情况，传统互补滤波算法无法准确地估算出载体的状态。本文所提出的混合滤波算法是在传统互补滤波算法的基础上，根据载体状态自适应调整滤波器状态参数，并将滤波后角速度向量作为强跟踪卡尔曼滤波算法的输入矩阵，通过比例因子自适应调整量测方差，混合滤波算法如图1所示。

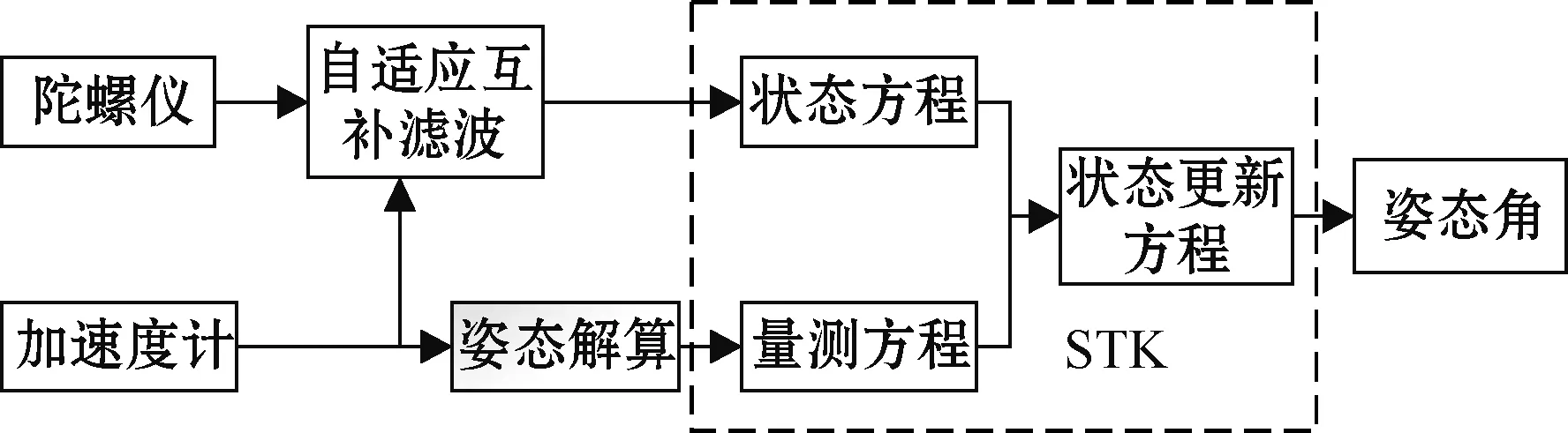
图1 混合滤波算法

3.1 自适应互补滤波

根据控制器参数对滤波效果的影响，积分常数KI主要是为了消除陀螺仪稳态误差，而KP调节低通滤波器和高通滤波器之间的截止频率[14]。本文将载体的运动状态分为3种：静止状态、低加速度状态和高加速度状态，根据载体状态自适应调整控制器参数KP。选取非重力加速度λ作为铁塔状态辨识量，用以判断当前时刻铁塔状态。

非重力加速度为

(9)

静止状态下加速度计量测值存在漂移现象，需要考虑加速度白噪声带来的影响。将惯性元件水平放置，读取加速度计测量的n组数据：

(10)

(11)

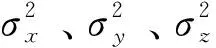
自适应互补滤波算法规则如下：

1)当λ≤ξ时，表明铁塔主部件处在静止状态，此时控制参数Kp，0=KP，其中Kp为比例系数初始值。

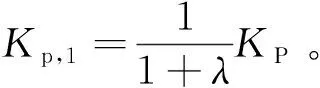
3)当λ>h时，表明铁塔主部件处于高加速度状态，此时加速度计测量结果不可靠，控制参数为KP,2=0。

自适应互补滤波算法如图2所示。

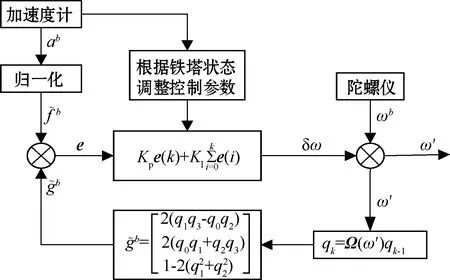
图2 自适应互补滤波

首先根据加速度值λ判别载体当前状态，调整控制参数；然后再根据互补滤波算法进行传感器数据融合，用以补偿陀螺仪角速度；最后由四元数矩阵Ω(ω′)更新当前姿态。

3.2 强跟踪卡尔曼滤波

强跟踪卡尔曼滤波以卡尔曼滤波为依托，当检测到量测异常时可由比例系数调整量测方差[15]，实现量测噪声方差自适应滤波。算法实现过程如式(12)～(20)所示。

1)预测过程:

(12)

(13)

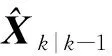
2)量测方差估计过程：

(14)

(15)

(16)

(17)

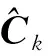
3)更新过程：

(18)

(19)

(20)

4 实验验证与分析

为了验证本文所提滤波算法的有效性，搭建实验平台采集数据，并通过Matlab仿真软件进行算法验证。实验设备包括三维转台与数据采集模块，如图3所示。设置单片机STM32F407ZGT6采样频率为100 Hz，用于采集MPU6050数据，并将数据通过串口的方式发送给上位机，实验原理如图4所示。

图3 三维转台

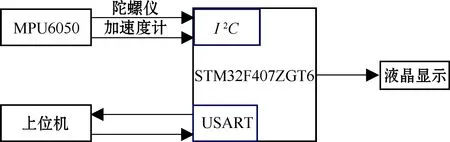
图4 实验原理

实验分为静态实验和摇摆实验两部分。本文将传统互补滤波算法、欧拉角卡尔曼滤波算法、自适应互补滤波算法、混合滤波算法进行对比。设定PI滤波器控制参数KP为1.2，KI为0.55。并以均方根误差(root mean square error，RMSE)来评价各种滤波的性能。均方根误差为

(21)

式中：xk为k时刻滤波解算出来的姿态角；x为真实姿态角；n为数据的长度。

4.1 静态实验

首先让转台处于水平位置，理想状态下俯仰角和横滚角均为0°。考虑到三轴加速度波动幅度较小，传统互补滤波算法与自适应互补滤波算法姿态解算结果几乎一致，所以静态实验只使用互补滤波、欧拉角卡尔曼滤波和混合滤波3种算法分别对横滚角和俯仰角进行解算。图5为横滚角解算结果，图6为俯仰角解算结果。可以看出，混合滤波算法解算结果均优于其他两种方法，其横滚角和俯仰角误差均小于0.05°。

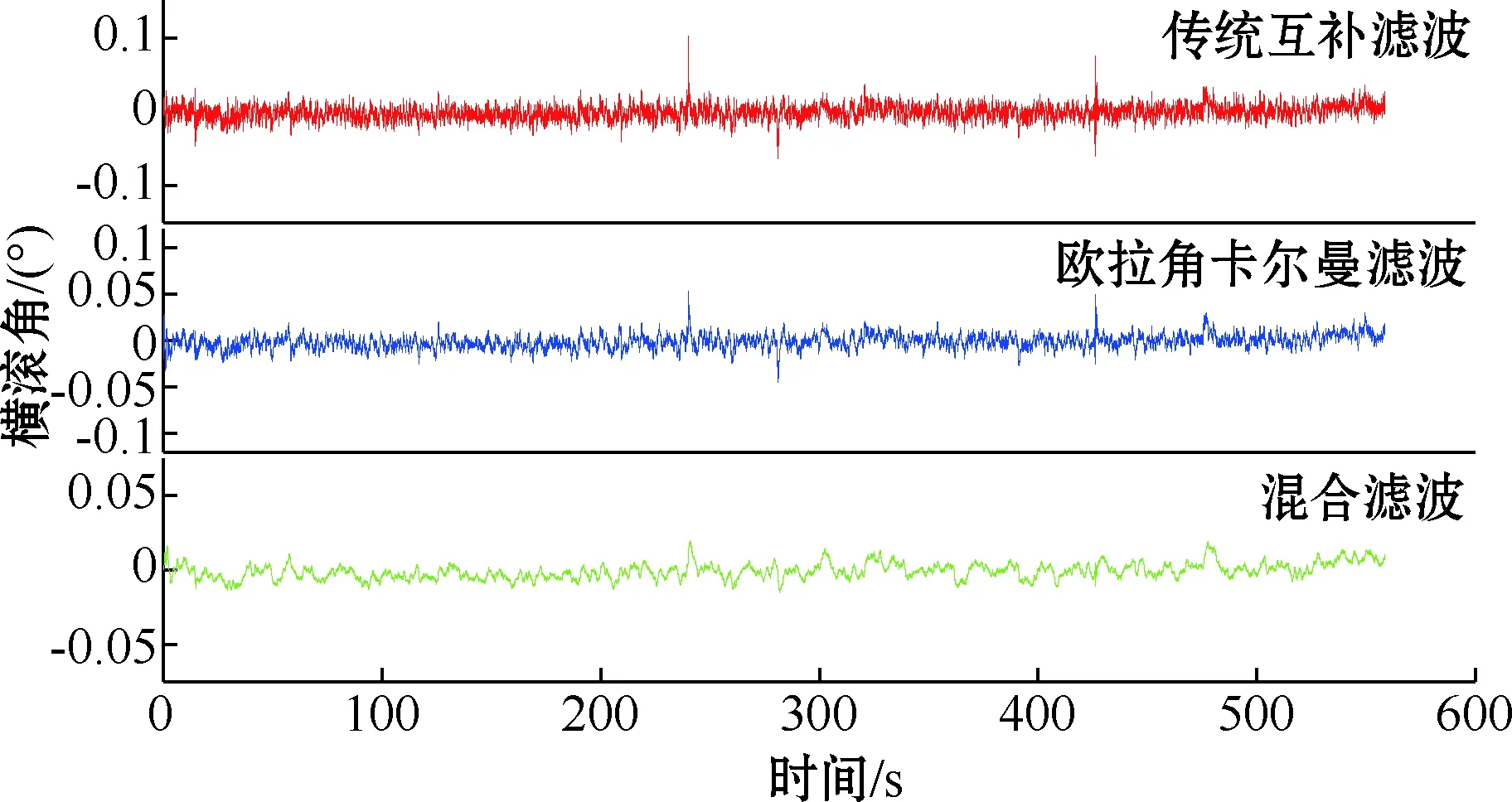
图5 静态横滚角解算结果

图6 静态俯仰角解算结果

表1给出了3种滤波算法姿态角均方根误差，其中传统互补滤波算法的性能最差，欧拉角卡尔曼滤波算法优于传统互补滤波算法，其整体RMSE约为传统互补滤波算法的72.00%。混合滤波算法抑制噪声效果最好，精度提升较大，其整体RMSE下降为欧拉角卡尔曼滤波算法的51.04%左右。

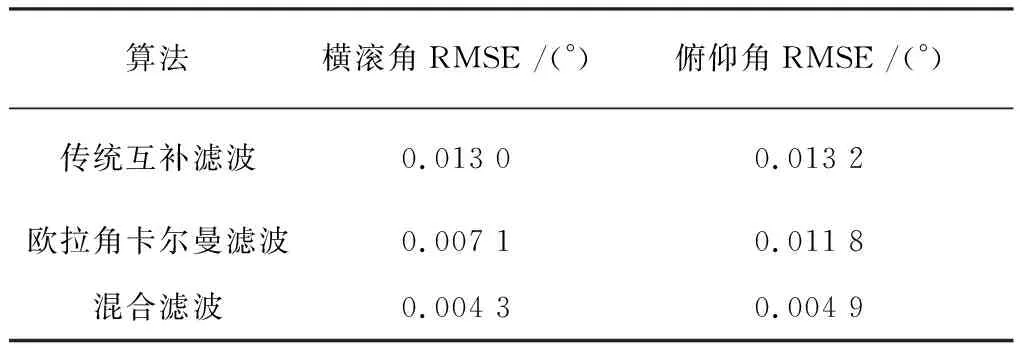
表1 静态实验姿态角均方根误差

4.2 摇摆实验

设计转台摇摆实验来模拟铁塔摆动，将惯性传感器固定在转台上，令转台分别绕横滚轴和俯仰轴方向做周期摇摆运动，设置摇摆幅值为3°，摇摆频率为2 Hz。分别采用欧拉角卡尔曼滤波、传统互补滤波、自适应互补滤波、混合滤波4种算法对载体姿态进行解算，其横滚角和俯仰角姿态解算结果如图7～8所示，局部放大图如图9～10所示。

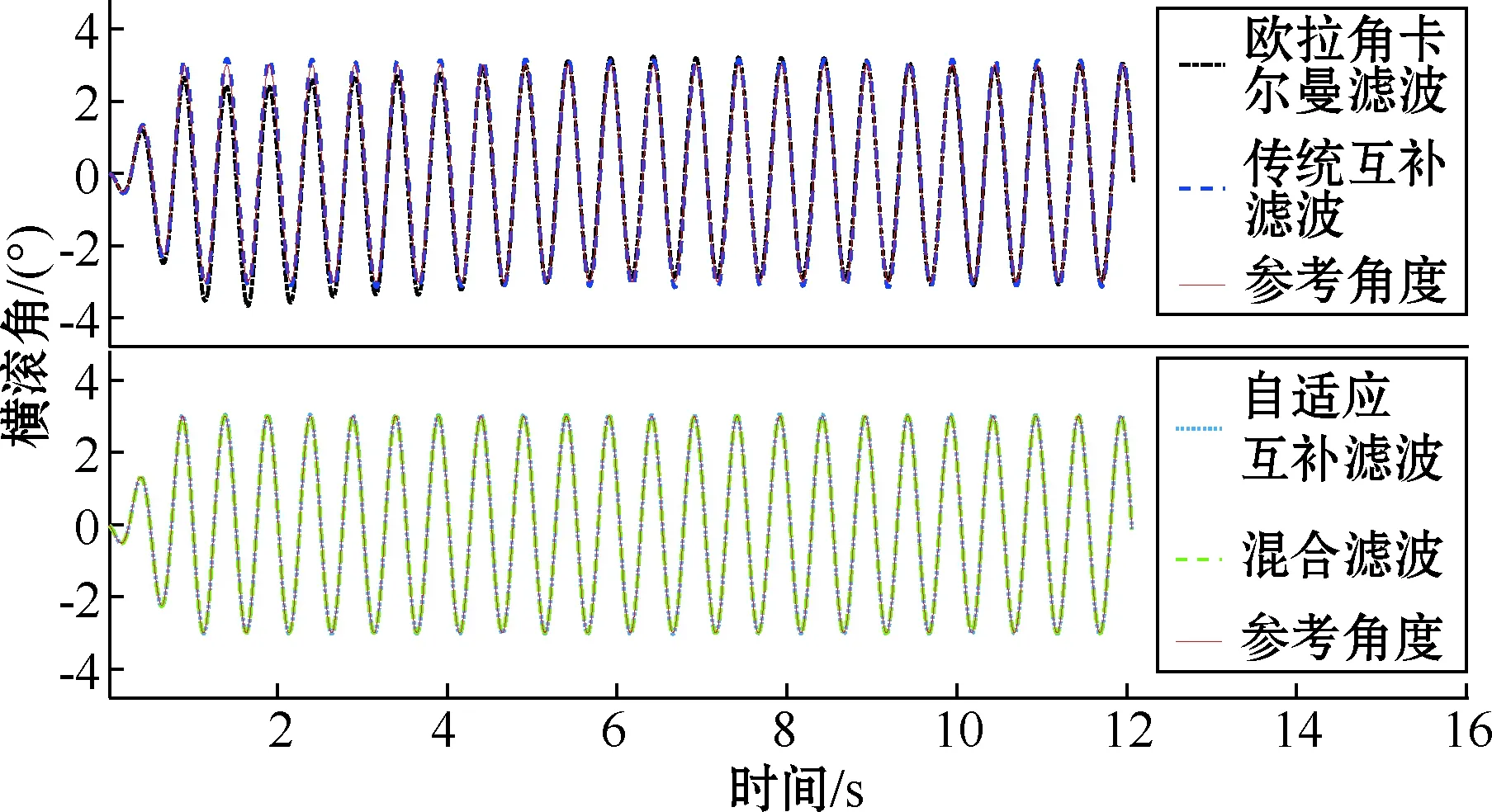
图7 转台摇摆横滚角估计

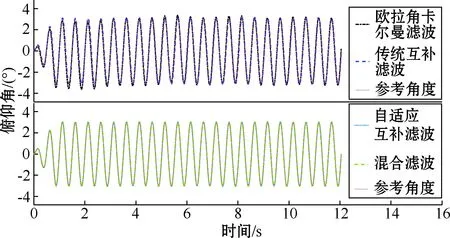
图8 转台摇摆俯仰角估计

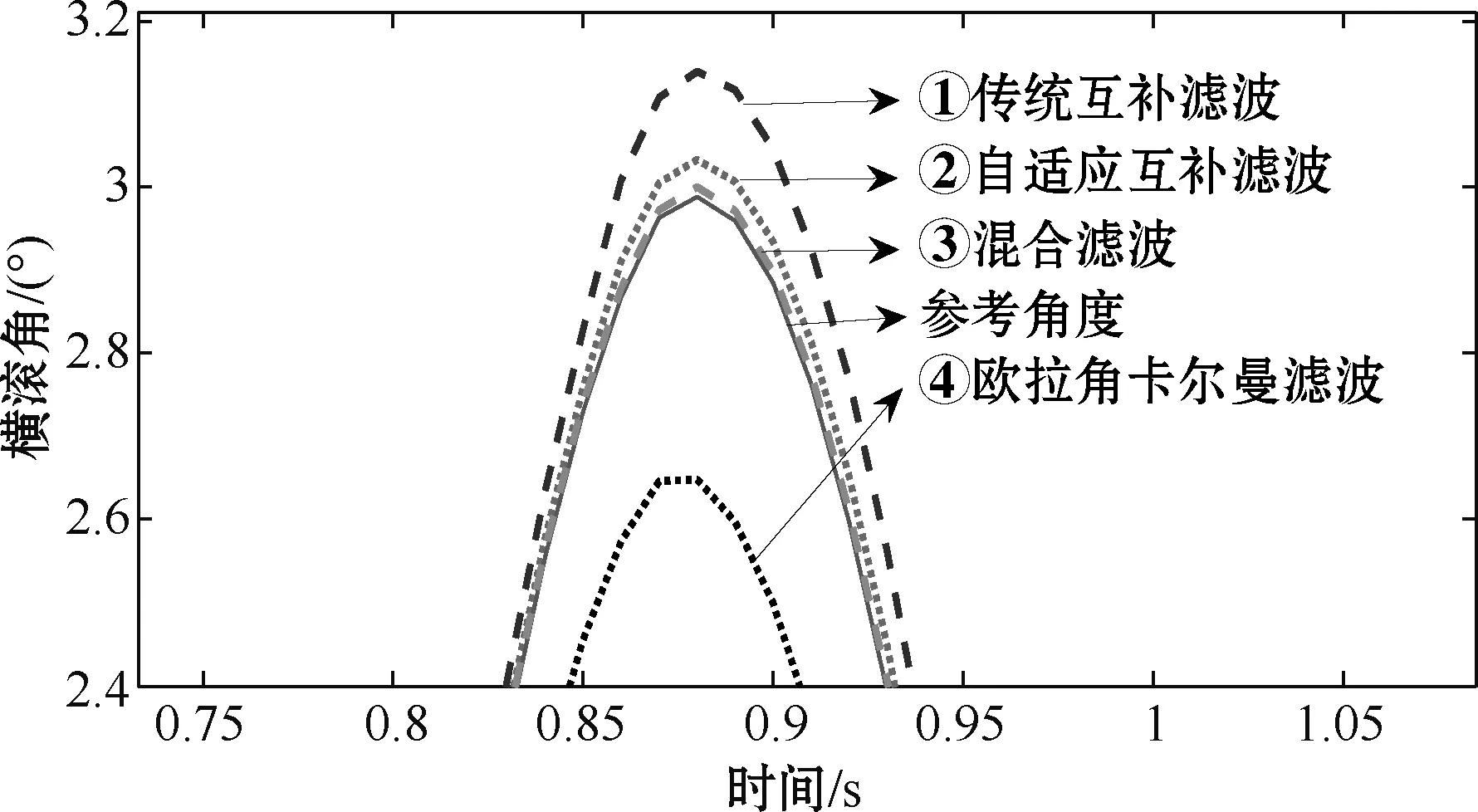
图9 横滚角局部放大图

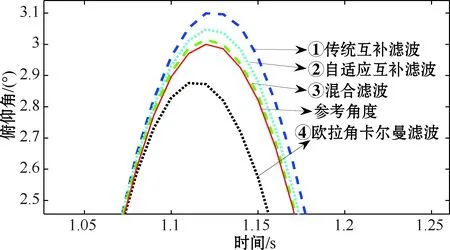
图10 俯仰角局部放大图

从图7～10中可以看出，欧拉角卡尔曼滤波和传统互补滤波算法解算的姿态角存在较大超调，自适应互补滤波算法根据载体当前非重力加速度自适应调整PI控制器，在一定程度上抑制了超调，然而在高动态环境中无法对当前噪声进行准确评估。混合滤波算法在自适应互补滤波作为状态值的基础上，通过对当前量测噪声进行估计，进一步提高了滤波效果。表2为4种滤波算法的均方根误差。

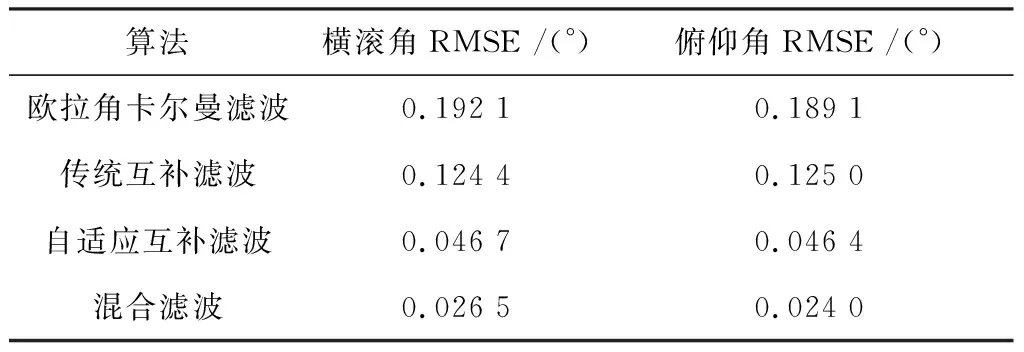
表2 摇摆实验姿态角均方根误差

从表2可以看出，在动态实验中传统互补滤波算法精度优于欧拉角卡尔曼滤波算法，自适应互补滤波算法整体精度相比于传统互补滤波有较大提升，整体RMSE仅为传统滤波算法的37.33%。混合滤波算法动态跟踪能力最好，整体精度最高，其整体RMSE下降到约为自适应互补滤波算法的54.23%。

5 结束语

针对传统的滤波算法存在姿态解算精度不高的问题，本文提出一种基于自适应互补滤波与强跟踪卡尔曼滤波的混合算法。在转台上设计静态和摇摆两组实验，对比了传统互补滤波、欧拉角卡尔曼滤波、自适应互补滤波以及混合滤波4种算法解算的精确度。实验结果表明，混合滤波算法无论在静态实验还是动态实验中均优于其他算法，其在静态环境中能够抑制姿态角波动，在动态环境中能够及时跟踪姿态变化，可满足对铁塔实时监测的任务需求。