Bose-Einstein凝聚问题基态解的数值方法比较和分析
曹 蕊,华冬英,王 茜,张读翠,李祥贵
(北京信息科技大学 理学院,北京 100192)
0 引言
玻色—爱因斯坦凝聚态是一种区别于人们所熟知的3种物质形态即气、液、固的新的物质状态。1924年,玻色提出新的光子的量子统计方法,爱因斯坦将其理论推广到带质量的理想气体,从理论上预言当温度在临界温度以下,玻色子(不存在相互作用的粒子)会在最低能量量子态上凝聚,达到可观数量时便形成凝聚态,这就是著名的玻色—爱因斯坦凝聚态(BEC)[1-2]。这些处于BEC的粒子具有宏观量子相关、隧穿和量子超流性等特殊的性质。随着激光冷却等技术的发展,关于玻色—爱因斯坦凝聚态的实验取得了突破性的进展[3-4],至此该研究领域飞速发展,数值模拟方法也在其相关的理论和实验方面发挥重要作用,其中计算BEC的基态、第一激发态以及动力学性质是BEC研究的基本问题。BEC现象的研究,不但在基础研究领域有着重要意义,同时在纳米技术、原子芯片技术、量子计算、原子干涉仪等领域有广泛的应用前景。近几十年来,关于BEC基态的一系列分析和数值研究,国内外学者们提出了很多不同的数值算法,其中广泛采用的是一种虚时法和投影法[5-6]相结合的方法,该方法使求解基态问题转为求Gross-Pitaevskii(简称G-P)方程最低能量问题,各种迭代格式可由不同的离散方法所得,比如向前/向后欧拉有限差分法,以及间断伽辽金法、时间分裂伪谱法[7-12]等。
本文针对G-P方程比较和分析两种数值计算方法求解玻色—爱因斯坦凝聚态的基态。对不同差分格式所得的完全离散格式分别采用完全非线性化迭代方法和线性化处理方法进行计算,最后对不同离散格式下两种算法的数值结果进行比较和分析。
1 问题介绍
非线性薛定谔方程是量子力学中的经典方程。本文将研究在温度远小于临界凝聚温度时描述玻色—爱因斯坦凝聚态的G-P方程求解基态解的数值方法。从模型的角度出发,考虑以下d(d=1,2,3)维的无量纲G-P方程:
β|ψ(x,t)|2ψ(x,t)x∈d
(1)
初始条件为
ψ(x,0)=ψ0(x)x∈d
(2)
式中:i 为虚数单位;x为空间坐标;t为时间;ψ为一个复值波函数;ψ0为给定的初值函数;Δ为拉普拉斯算子;V(x)≥0为一个实值电势;β∈为一个任意的无量纲参数,它表示粒子间相互作用强弱。式(1)中波函数有两个重要的不变量,即质量 (归一化即单位化后)
(3)
和粒子能量
E(ψ(·,0))t≥0
(4)
为找到式(1)的稳态解,把稳态解ψ(x,t)表示为
ψ(x,t)=φ(x)e-iμt
(5)
式中:μ为化学势;φ为一个与时间无关的实函数。将式(5)代入式(1)中,可得:
β|φ(x)|2φ(x)x∈d
(6)
在归一化条件下:
(7)
可以看出式(6)的本质是带约束条件式(7)的非线性特征值问题。特征值μ可由其对应的特征函数φ(x)表示为
(8)
式中E(φ)为式(4)中给出的与φ相关的能量函数。
2 数值方法
在实际计算中,由于G-P方程(1)的解在远场快速衰减,具有齐次Dirichlet边界条件,通常选择截断域足够大则截断误差可忽略不计。为叙述及计算方便,本文只考虑空间一维的情况,则上述式(1)连同初始条件式(2)中x的范围可以取成Ω=[a,b]。以下讨论同理可推广到二维和三维的情况。目前虚时法是计算G-P方程基态解的常用方法之一,即用-t替换式(1)中的it,使其变为能量耗散的方程:
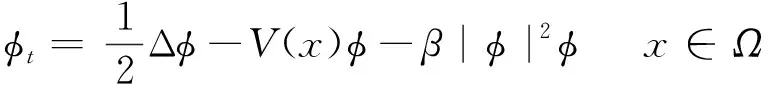
(9)

为保证归一化条件式(7)成立,实值波函数φ在离散的每个时间间隔结束时,通过投射至单位球面来对该解进行归一化处理,即将时间步长设为Δt>0,时间方向进行剖分tn=nΔt(n=0,1,2,…),在每个时间间隔[tn,tn+1]结束时让波函数对单位球面作投影,即
(10)
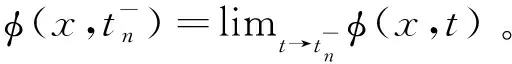
φ(x,t)=0x∈∂Ω
φ(x,0)=φ0(x)x∈Ω
2.1 空间离散
为方便起见,对一维空间区域Ω=[a,b]进行等距剖分,正整数J表示剖分总数,设置节点下标的集合为:
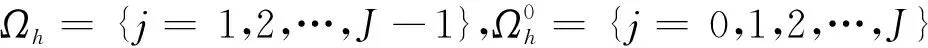
在空间方向上使用经典的二阶中心差分对式(9)进行离散,可得式(9)的半离散格式为
β|φj(t)|2φj(t)j∈Ωh
(11)
式中Vj∶=V(xj),初始条件及边界条件分别为
φ0(t)=φJ(t)=0
2.2 时间离散

2.2.1 向后欧拉格式
在时间方向上使用向后欧拉格式进行离散得式(9)的完全离散格式:
(12)
初始条件及边界条件分别为
(13)
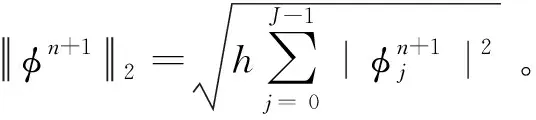
此数值格式离散的能量和化学势可表示为:

(14)
则上述离散方程就转为更简单的线性方程组求解,可直接采用追赶法。这种处理方法简洁有效,但终究还是回避了原来更精确的格式(12)求解,所以本文仍采用原离散格式(12)进行计算。对式中非线性项的处理设计一种算法——迭代求解法,此方法在理论上更直接,也符合实际理论要求。具体操作如下:
取整数m≥0表示迭代次数,离散格式(12)的迭代方法为:
(15)
根据式(15),假设在第n个时间层t=tn时的数值解已知,求解第n+1个时间层时,将未知变量移到等号左侧,已知变量移到等号右侧,化简得
(16)
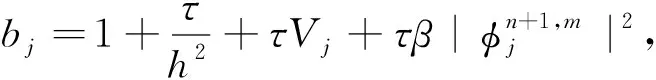
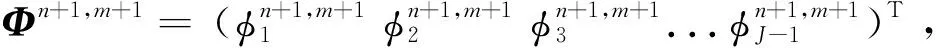
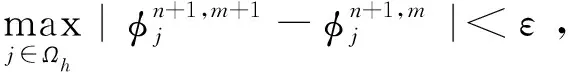
2.2.2 Crank-Nicolson格式
(17)
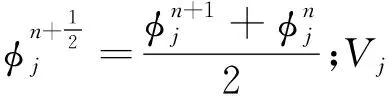
该数值格式的能量和化学势为:
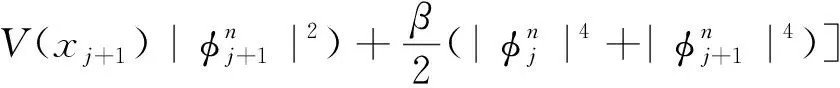
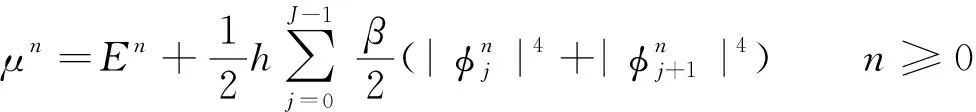
(18)
式(18)可直接用追赶法进行求解。
同样地,式(18)的计算过程回避了式(17)中原本的非线性项,理论上式(17)可使用迭代求解法直接进行求解,具体步骤为
(19)
假设tn层数值解已知,求解tn+1层,化简式(19)整理得
(20)
令
则有
令
则AΦn+1,m+1=Kn
式中

3 数值计算比较与分析
本节通过数值算例对上述数值算法进行比较与分析。

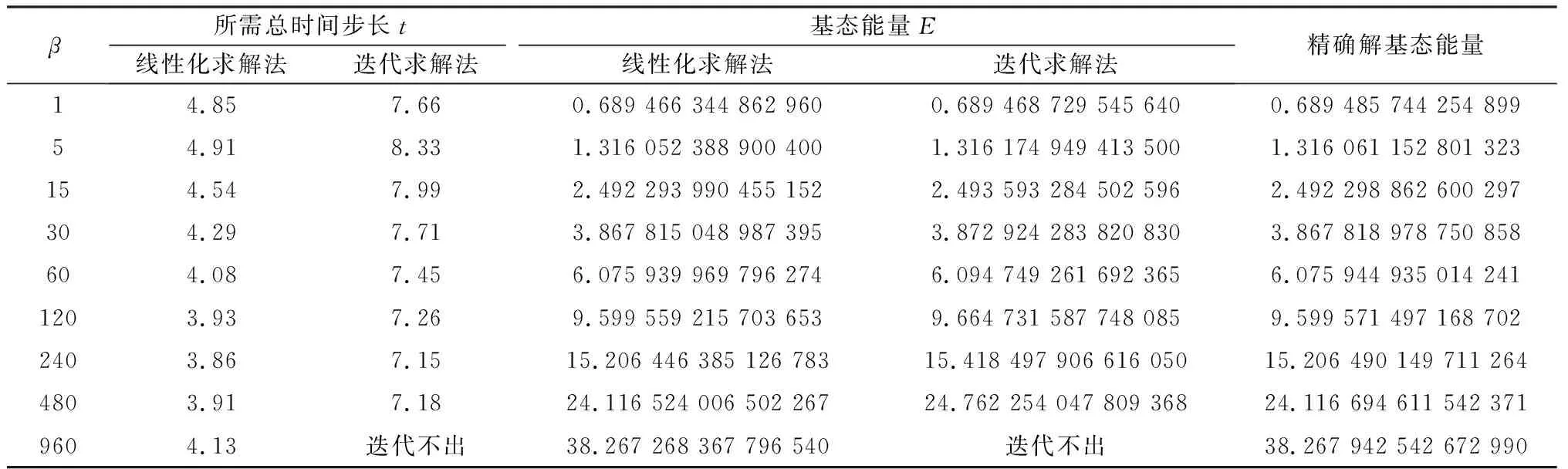
表1 向后欧拉格式——两种算法在不同β下所需总时长t和基态能量E的对比表

图1 β=60时,向后欧拉格式—能量随时间的演化
由表1可见,在此步长取值下,若β取值过大,迭代求解法失效。以下是简单分析:
由于β很大,式(9)右端前两项的作用可忽略,仅考虑非线性项作用:
-βφ3(x,t)tn≤t≤tn+1
(21)
计算得
(22)
此时tn+1-tn=τ。当β很大,而τ不变,则左端变大,而对于同一时间层上相邻的φn,m+1和φn,m相差很小,就可能会出现不匹配的问题,从而出现迭代失效。所以当β较大的情况下,τ的取值需要相应更小,才可保证算法顺利进行。
由图1、图2可以看出在该步长取值下,比起线性化求解法,迭代求解法误差更大。进一步详细分析当β=60时两种算法在不同h和τ的取值下的计算结果,如表2和表3所示。
由表2、表3可以看出,使用向后欧拉格式时,线性化求解法对时间步长和空间步长的取值要求不高,迭代求解法更容易受时间步长大小的影响,需较小的时间步长才可保证迭代顺利进行。
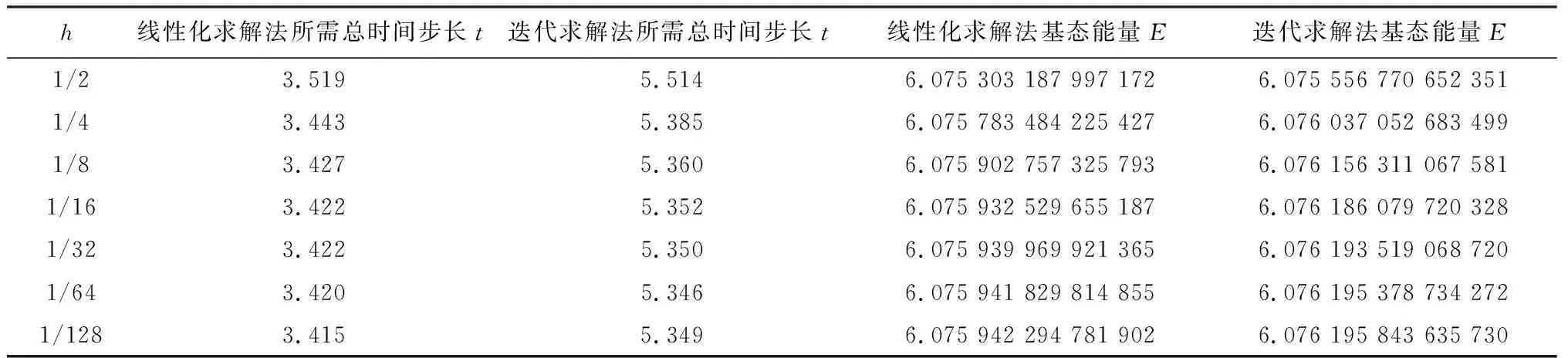
表2 当τ=0.001时向后欧拉格式——两种算法在不同空间步长下对比表

表3 当h=1/128时向后欧拉格式——两种算法在不同时间步长下对比表
使用C-N格式计算时,取与向后欧拉格式中相同的步长作为精确解,同样发现在固定的网格比(τ=0.01,h=1/32)下,若β取值过大则迭代求解法无法求解,需取更小的时间步长来保证该算法求解顺利。当β=60时,在固定网格下使用C-N格式,两种算法计算结果如图3、图4所示。同样出现迭代求解法误差比起线性求解法更大的现象。为进一步详细分析,使用C-N格式时,用两种算法在不同h和τ的取值下的计算结果如表4和表5所示。
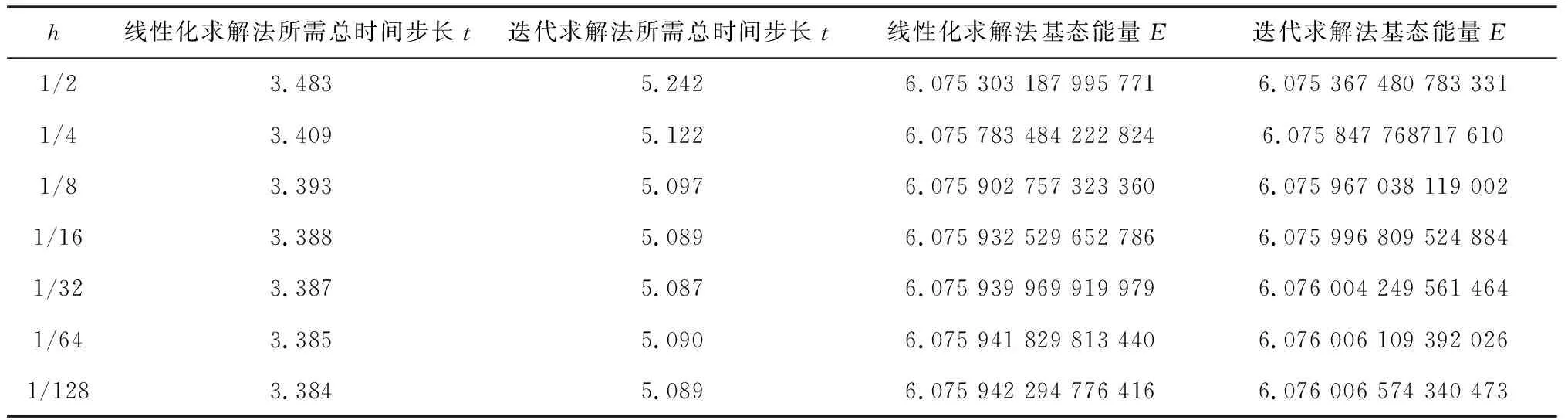
表4 当τ=0.001时C-N有限差分格式——两种算法在不同空间步长下对比表
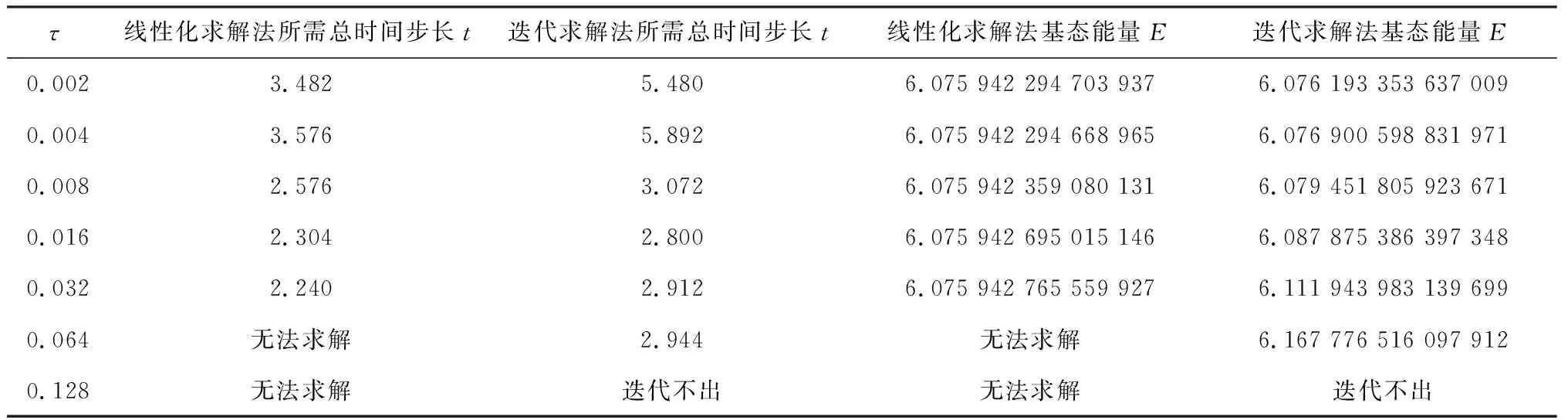
表5 当h=1/128时C-N有限差分格式——两种算法在不同时间步长下对比表
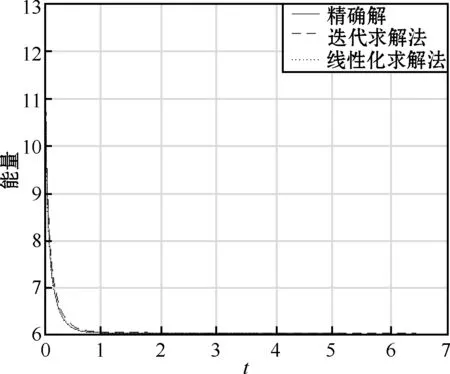
图3 C-N格式-能量随时间演化
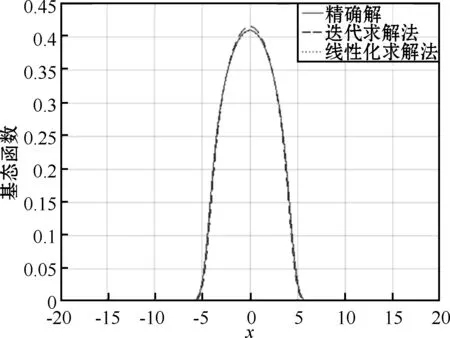
图4 C-N格式 - 基态解
综合数据可以看出,在相同网格比和时间步长情况下,C-N格式比向后欧拉格式计算时间要短。当时间步长变大时,向后欧拉格式能量耗散更稳定,而C-N格式会出现不稳定情况。以下是简单分析:
根据泰勒展开式,可得向后欧拉格式和C-N格式的数值近似分别为
(23)
(24)
可以看出式(23)中右端第2项是数值耗散项,式(24)中右端第2项是数值色散项,数值耗散会使所求基态解变得平滑,数值色散会使所求基态解振荡。在例1中,通过实际数值测试,使用向后差分格式时,τβ的值控制在0~0.07;使用C-N差分格式时,τβ的值控制在0~0.14,可保证在相同β下取不同的τ使用迭代求解法求得的基态解误差在10-3内。
结合上述可知,无论是向后欧拉格式还是C-N格式,线性化求解法和迭代求解法这两种算法均可以用于求解基态解,两者计算的能量都随时间演化呈衰减趋势。在同样较小的时间步长下两种算法的计算结果较为接近,使用迭代求解法进行计算是符合理论要求的。但在β变大时,往往需要取比线性求解法更小的时间步长τ才能使迭代求解法顺利进行,且所求结果更为准确,而使用线性化求解法计算效果相对稳定,在使用向后欧拉格式的时候无步长取值要求,总体而言所需总时间步长更少。
4 结束语
本文利用虚时法加投影法求解G-P方程的基态解,分别对向后欧拉差分格式及C-N差分格式的两种数值计算方法进行分析和比较。提出的迭代求解法进行数值计算更符合理论要求,并且结果更为精确,但此求解过程需要根据β的大小来取适当的时间步长τ的值。而线性化求解法稳定性较高,求解所需时间更短,实际数值算例验证了分析结果。该讨论与分析结果只针对本文一维G-P方程,其他G-P方程的结果还需进一步的讨论与分析。
——中国制药企业十佳品牌

