基于U模型的滑模增强控制方法

李文清，王志强

(航空工业西安飞机工业集团股份有限公司，陕西 西安 710089)

系统建模在基于模型的控制系统设计中发挥着至关重要的作用[1-2]。通常，实用新型和控制系统有两个主要的重要考虑因素：① 面向控制性能，增强控制系统的准确性和鲁棒性；② 面向控制结构，简化控制系统的设计步骤和减少计算量。

对于第一个关注点，在实际情况下，即使在学术研究中，也很少有模型能够准确地代表实际被控对象，因此基于模型的控制系统设计应考虑模型内部不确定性和外部干扰(例如系统扰动)[3]。滑模控制[4]已经被证明可以有效地用于处理可变结构系统(即涉及不连续控制动作的控制系统)中的不确定性。滑膜控制方法的优势在于：首先可以通过选择切换函数来调整系统的动态性能[4]；其次，即使系统存在外部干扰和被控对象模型内部不确定的参数项，滑模控制方法也可以保持被控系统的稳定性并具有很强的鲁棒性。如今，滑模控制技术已经在各种领域中发展，例如积分滑模控制方法[5]、二阶滑模控制方法[6]、超扭曲滑模控制方法[7]和自适应滑模控制方法[8-9]。

对于第二个问题，本研究中使用的关键思想是基于U模型的控制方法，简称U控制方法。U模型是一种面向控制的模型，它代表一类平滑系统，该系统使用时变参数和函数吸收系统输入u及其相对高阶导数项以外的所有其他项。通常，可以将这种新颖的U模型转换并表达为单层和多层模型，即线性和非线性系统的多项式模型和状态空间模型。朱全民等[10]首先提出了U型控制器的基本设计程序，通过使用牛顿-拉夫逊算法求解控制器输出函数的根来直接获得所需控制器输出u。文献[10]定义了U模型的多项式表达形式，并通过极点配置方法介绍了U控制系统的框架和设计步骤，还提供了从一般光滑线性/非线性系统到基于U模型的表达式的转换方法。之后，U模型在当前控制项中扩展NARMAX(Nonlinear Auto-Regressive Moving Average with Exogenous Inputs)函数作为幂级数，从而允许将简单的多项式根求解过程与控制器综合。通常，U控制方法可以避免非线性系统建模过程中的线性化处理，从而优化了控制系统的设计步骤，减少了计算量。但是，基于U模型的动态反演和控制性能对被控对象模型内部不确定性以及系统控制扰动非常敏感，在这种情况下，降低U控制方法对不确定性的敏感度、提高其鲁棒性成为当前研究的热点。

近十年中，学者们对基于U模型的控制方法进行了大量研究，提出了基于U模型的极点配置控制系统设计方法[11]，用于控制复杂非线性动态系统的自适应U模型控制方法[12]和基于U模型的神经网络增强控制方法[13]。但是，大多数U控制方法都要求精确的被控对象建模和完全匹配的可用系统。因此，基于U模型的鲁棒控制方法在研究中是非常必要且具有挑战性的。文献[14]和文献[15]使用内模控制结构(Internal Model Control,IMC)增强U控制的鲁棒性并对无人水下航行器进行控制且取得了良好的控制结果。但是因为精确非线性模型求逆困难，IMC的结构限制了这类控制方法应对强非线性系统的能力。同时，连续时间U控制系统的设计也很少有人参与[16]，这是因为受控系统的输入和输出的高阶导数项在连续时间条件下的动态反演很难解决。

综上所述，滑模控制系统鲁棒性能优越，但其设计结构复杂且运算量大，当滑模控制系统需要参数调整时，需要重新设计滑模面或切换函数；同时现存的结合U模型的控制系统受限于内模控制结构而无法应对强非线性。因此，本研究面对这两个挑战，尝试结合U模型面向控制的特点和滑膜控制方法的强鲁棒性，以开发出一种新的基于U模型的滑(Sliding Mode)模增强控制方法(以下简称U_SM控制)，旨在解决一类控制对象可逆且控制系统存在建模误差和系统干扰的控制问题。

笔者基于U模型定义和U控制的实现方法，结合滑膜技术提出了一种基于U模型的滑模增强(U_SM)控制方法。该控制方法同时包含面向控制的模型结构和针对不完美匹配控制对象的强鲁棒性，并在简化的直升机俯仰角仿真控制案例中进行验证，其结果证明了该方法可对开发的控制系统进行基础测试。

1 U模型和U控制

1.1 U模型的多项式结构

对于一个由(y,u,λ)组成的单输入单输出U多项式模型，定义如下：

(1)

式中，y(M)为控制平台输出y的M阶导数；u(N)为控制器输出u的N阶导数。λj(YM-1,UN-1,Θ)∈R+是时变参数，吸收除输入(u(N))j之外的其他项，如：YM-1=[y(m-1),y(m-2),…,y]∈RM,UN-1=[u(n-1),u(n-2),…,u]∈RN和系数Θ。

备注1：U多项式是经典多项式的替代表达，具有时变参数和面向控制的结构。

以经典的NARMAX多项式模型为例，其U模型实现过程如下：

(2)

其基于U模型的相对表达式为

(3)

通过观察式(2)和式(3)，很明显U多项式模型是经典多项式模型的直接实现。需要注意的是，U多项式模型在模型属性上与其对应的经典多项式模型相同，但是对于控制系统设计，特别是复杂的非线性系统，U多项式模型的结构和表达方式较为简洁[12]。

备注2：应用吸收规则[16]，可以将经典多项式模型转换为U多项式模型，即用时变参数λj吸收所有与系统输入u相关的函数关联项。

备注3：在U多项式模型式(1)中，很明显当阶数J=1时，式(1)可以转化为U多项式模型的线性结构：

y(M)=λ0+λ1(u(N)),M≥N

(4)

1.2 扩展的U多项式模型

扩展的U多项式模型也称U-Rational(简称U_R)模型，可以定义为两个U多项式模型的比值，其结构可表示为

(5)

式中，fnj和fdj分别为式(5)分子和分母项中吸收控制器输出u(N)的平滑函数；λnj和λdj则分别为吸收式(5)分子和分母中除控制器输出u(N)以外的所有其他项。考虑一个简单的复杂多项式模型以显示其从经典模型到U模型的转换过程：

(6)

因此，其U多项式拓展模型为

(7)

其中：

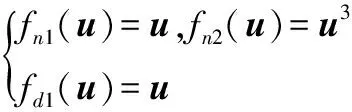
(8)

1.3 U状态空间模型

U状态空间(State Space)模型，简称U_SS，定义如下：

(9)

式中，λ**为U模型的时变参数，可以吸收除了控制器输出u以外的所有其他项；而f**为一个基于u的函数。

备注4：由于U状态空间模型(式(9))中的每一行都是一个U多项式模型(式(1))，所以U状态空间模型本质上是多层的U多项式模型。

考虑一个简单的非线性状态空间模型：

(10)

根据式(9)中的吸收规则，将非线性状态空间系统(式(10))转换为U状态空间模型：

(11)

1.4 基于U模型的控制系统框架[16]

‖GP(x1)-GP(x2)‖≤γ1GP‖x1-x2‖

∀x1,x2∈Rn

(12)

式中，γ1和γ2为Lipschitz系数。

图1 U控制系统设计框架

(13)

在这种情况下，系统输出y将直接受被控对象建模比率k的影响。当闭环控制系统中Gc1很大时，系统扰动d的影响将被抑制。但是，如果系统存在高频干扰，则不仅会影响控制系统的性能，还会由于共振而损坏控制系统。综上所述，被控对象的建模不准确和系统扰动都将给U控制系统设计带来巨大的困难和挑战。

2 U_SM控制系统的框架和设计步骤

在第1节中，由于被控对象的建模不准确和系统扰动这两个主要问题极大地降低了U控制系统的控制性能，因此本研究提出了一种新的滑模增强控制方法，即U_SM控制方法，该方法将U控制和滑膜控制相结合以增强U控制的鲁棒性。U_SM控制系统框架如图2所示。

图2 U_SM控制系统框架

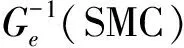
根据1.4节中的U控制系统设计框架，用实际被控对象模型GM替换U控制系统中的理想被控对象模型GP。因此，系统(式(13))可以转换为

(14)

(15)

(3)设计不变控制器Gc1。

图3 简化的U_SM控制系统

Σ=(Gc1,1)

(16)

(17)

考虑一个单输入单输出连续状态空间模型如下：

(18)

式中，u,y∈R分别为被控对象的输入和输出；X∈Rn表示所有的状态变量；F∈R引入了状态变量和被控对象输入之间的关系；H∈R是将所有状态变量映射到被控对象输出的平滑映射。将此状态空间模型(式(18))展开为多项式结构：

(19)

3.1 理想逆变器的设计

忽略状态空间模型(式(19))中的控制干扰d，并将其转换为多层U模型表达式(12)：

(20)

对式(20)中的y进行微分运算，得到：

(21)

y(m)=λ1(x1,x2,…,xn-1,xn)+λ2(x1,x2,…,xn-1,xn)ui

(22)

式中，λi为吸收所有状态变量的时变参数。显然，式(22)是通用U模型多项式表达式(式(1))的简化形式。因此，理想的U模型动态逆变器输出ui为

(23)

3.2 补偿逆变器的设计

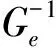
(24)

σ=c1e1+c2e2+…+cm-1em-1+em

(25)

根据式(25)，表面滑动函数的导数为

(26)

式中，ci∈R为指定的表面滑动函数的带宽系数[4]。

(27)

(28)

(29)

在这种情况下，式(28)可以展开为

(30)

(31)

(32)

根据式(23)和U_SM控制系统框架(式(14))，除不变控制器Gc1外，U_SM控制器输出应包含两部分：理想逆变器输出ui和补偿逆变器输出us，且us=ueq+usw。然后将U_SM控制器输出us带入式(30)：

(33)

≤-ρ|σ|-kσ2≤0

(34)

4 实验仿真测试

在本节中，选择简化的二自由度直升机俯仰动力学模型来测试所提出的U_SM控制方法。使用Matlab/Simulink展示仿真结果。

4.1 简化的直升机俯仰动力模型

实验直升机实物模型如图4所示，简化的二自由度直升机模型[18]示意图如图5所示。因建模仿真计算过程只使用点积运算，因此将所涉及变量简化为标量进行处理。简化后的直升机俯仰动力学非线性模型可以由以下方程式描述：

图4 直升机实物图

图5 直升机的简化俯仰模型[18]

(35)

(36)

式中，x1为俯仰角θ；x2为俯仰角速度ω；Iyy为绕y轴的二阶矩阵；mhel为直升机的质量；lcgx和lcgz分别为与机身水平和垂直的从旋转关节B到质量中心点(图5中的CG(Center of Gravity))的距离；FvM为俯仰阻尼；u为直升机主叶片绕y轴施加的控制扭矩；g为重力加速度。

4.2 设计不变控制器Gc1

系统(式(36))被设计为一个临界阻尼系统，它可以使被控对象尽可能快地达到平衡状态(期望的输出)而不会产生超调。参照第2节中提出的U_SM控制系统设计步骤，本研究选择系统阻尼率ζ=1和固有频率ωn=2。因此，所需的闭环系统增益为

(37)

参考1.4节和2节，通过计算闭环传递函数(式(37))的逆函数来确定不变控制器Gc1：

(38)

4.3 设计理想逆变器

(39)

因此，原始系统(39)可以转换为U模型表达式：

(40)

(41)

(42)

4.4 设计补偿逆变器

根据3.2节，误差方程设计为

(43)

其相应的滑动函数定义[4]为

σ=ce1+e2

(44)

根据式(43)和式(44)，求得滑动函数的导数：

(45)

将式(40)带入式(45)，可以得到：

(46)

(47)

usw=-(εsgn(σ)+kσ)

(48)

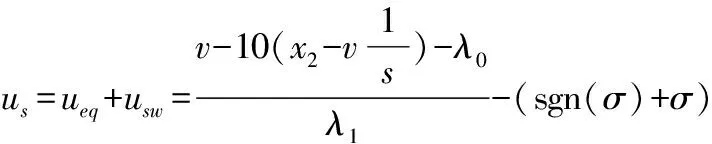
(49)

为避免系统震抖[19]，如果系统滑入边界ξ∈R+，则控制器输出不应存在切换函数。定义开关函数为

(50)

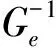
(51)

4.5 测试完美匹配的直升机模型

基于文献[18]，直升机实验建模参数如表1所示。

表1 直升机特性的俯仰模型

对于U模型(式(40))，很明显，基于U模型的时变参数为

(52)

应用U_SM控制方法设计的理想直升机模型控制系统框架如图6所示；图7显示了基于U控制和U_SM控制方法控制的理想简化直升机模型的比较结果；图8显示了补偿逆变器的输出。

图6 理想直升机模型的U_SM控制系统框架

图7 完全匹配的简化直升机模型的控制结果比较

图8 理想控制模型下U_SM补偿逆变器输出

4.6 鲁棒性测试和比较

4.6.1 控制具有内部不确定参数的简化直升机模型

在实际的控制系统操作中，闭环系统的输出可能无法准确测量，并且可能与模型不完全匹配。因此，为了适应这种不准确性，系统(36)更改为

(53)

式中，Φ为系统不确定系数，其变化范围为0.5～1，其变化频率为1 Hz。图9显示了其变化曲线。

图9 系统不确定系数变化曲线

备注5：Φ在其边界内随机变化。因为其变化范围为0.5～1，所以该不确定系统与完全匹配系统的偏差为0%～50%。为了避免震抖，ξ应该设计的比之前大。令ξ=0.1，则此时的开关函数为

(54)

应用U_SM控制方法设计的具有系统不确定性的直升机模型控制系统框架如图10所示；图11显示了使用U控制方法和U_SM控制方法对带有内部不确定参数的简化直升机模型控制的比较结果；图12显示了补偿逆变器的输出。

图10 带有内部不确定参数的直升机模型U_SM控制系统框架

图11 带有内部不确定参数的直升机模型控制结果比较

图12 实际控制模型下U_SM补偿逆变器输出

4.6.2 控制具有系统扰动的不确定直升机模型

考虑一个更复杂和实际的控制情况：在实际建模过程中不仅存在系统内部不确定性，并且控制器与受控平台之间的接口处存在系统噪声。因此，为了适应这种误差，系统(53)改进为

(55)

式中，d为系统扰动，其变化范围为0～0.3，变化频率为10 Hz。与系统(53)一样，Φ的变化范围为0.5～1，变化频率为1 Hz。图13显示了系统扰动的变化曲线。

图13 系统控制扰动的变化曲线

备注6：Φ和d在其边界内随机变化。在该系统中，基于图7(d)所示的完全匹配情况下的U控制器输出，很明显，当控制器输出较小时，系统扰动将极大地影响系统的稳定性和其控制性能。系统的边界系数设计与系统(55)相同，令ξ=0.1，则开关函数为

(56)

图14显示了控制具有内部不确定参数和系统扰动的直升机模型的U_SM控制系统设计框架；图15显示了使用U控制方法和U_SM控制方法对其控制的比较结果；图16显示了补偿逆变器输出。

图14 带有系统扰动和内部不确定参数的直升机模型U_SM控制系统框架

图15 带有系统扰动和内部不确定参数的直升机模型控制结果比较

图16 U_SM补偿逆变器输出

4.7 讨论

对于控制完全匹配的直升机模型，从图7(a)和图7(b)中可以看出，两种方法都可以使受控系统收敛并跟踪所需的参考输出信号。另外，从图7(c)和图7(d)中可以看出，在模型完全匹配的情况下，这两个系统的控制器输出也相同，即补偿逆变器输出为0，这同样可由图8看出并得到证明。补偿逆变器输出为零意味着补偿逆变器仅在系统存在干扰时工作，如果被控对象建模准确且控制系统中没有干扰，则U_SM控制方法将具有与U控制方法相同的受控能力和性能。

从图11(a)和图11(b)可以看出，为了控制存在内部不确定参数的直升机模型，在跟踪能力上，U_SM控制方法的性能优于U控制方法。从图7(d)和图11(d)可以看出，在完全匹配和不匹配的情况下U控制器的输出几乎相同，但是由于被控对象的差异，不匹配直升机模型的控制性能会下降。

关于参数调整，在不变控制器Gc1中，不同的阻尼比ξ和固有频率ωn可以令控制系统实现不同的追踪性能；系统的鲁棒性则主要由基于滑模技术的补偿逆变器决定，即式(32)中的ε，其中ε与系统鲁棒性和控制器输出震抖幅度均成正比关系。

5 结束语

介绍了一种新的滑模增强U模型控制方法(U_SM控制)。在信号跟踪方面，该方法在对于不确定模型和存在系统扰动的控制中展示出强大的稳定能力。滑模增强U控制方法的总体方案基于U控制结构，通过结合滑模控制与U控制引入动态补偿逆变器以增强U控制的鲁棒性。这项工作能够将滑模控制方法的强鲁棒性与U控制的模型独立性设计理念相结合，以提供全面的简单的不确定扰动系统控制方案。

对于未来的研究工作，首先，应该对所提出的U_SM控制方法进行进一步的分析与测试，以找出其控制优势和劣势。同时，本研究中的U_SM控制方法仅面对控制单输入单输出系统，对于多输入多输出(MIMO)系统的研究还不足。尤其对于欠驱动和过驱动系统，逆变器的设计与实现存在明显的困难与挑战。