自由射流高空模拟试车台系统建模与仿真研究

姚艳玲，袁化成，吴 锋，冷林涛

(1.南京航空航天大学，江苏 南京 210000；2.中国航发四川燃气涡轮研究院，四川 绵阳 621000)

自由射流/常规高空模拟设备运转时，进气系统、排气系统、试验舱之间存在很强的物理耦合关系，为了对整个系统的运转状况、参数分布、逻辑顺序进行研究，除了设备调试试验外，还需要建立相应的数学仿真模型加以辅助。

从仿真维度上来说，通常的数值研究手段有0/1维、二维、三维求解算法。通常二维、三维适用于对小尺度、短时间、稳态物理过程的模拟，不利的一点是，如果将复杂系统整体建模，其计算网格量将相当惊人，但如果分部件计算，其边界条件的给定将很难反映实际系统之间的耦合性；而0/1维求解算法则恰恰避开了这些问题，适用于解决那些系统维度大、复杂度高、耦合性强的系统级仿真问题。

使用的系统仿真技术就是一种0维多学科数值仿真技术，它通过利用非因果建模技术(不显性指定求解方向)来达到描述系统中各个子系统的特性并反映系统综合效能的目的。比如，利用系统仿真技术可以轻松求解过渡态容积填充时间、压力平衡稳态、流量瞬变动态响应、发动机喘振频率模拟等问题。

正如发动机总体性能专业为了研究发动机循环参数而建立发动机性能模型一样，高空台设备也应该具有一套可以用于研究设备试验能力、试验技术的仿真模型，正是从这一点出发，以自由射流试验技术为背景，开展相应设备的数学建模仿真工作。

1 建模仿真关键技术

数学建模一般分为3种方式：面向信号的建模、面向物理对象的建模和基于方程和算法的建模。面向信号的建模需要将所有领域的计算变量(压力、温度、流量、电信号等)统一称为数字信号，用类似搭建电路的方式构成系统的输入输出。基于方程和算法的建模需要为程序指定计算求解方向，系统稍有结构修改就得大幅修改代码。而面向对象的建模方式是现在最流行最为常用的一种建模方式，它主要基于基本元素组合的建模理念，即是把物理系统分解为最小元素，通过搭积木的方式搭建复杂系统，以尽可能详细和精确地描述零部件以及由它们构成的复杂工程系统。

面向物理对象的建模方式之所以能体现易用性、直观性、普适性，是因为解决了以下3个关键技术问题：① 经采用数学方程而不是赋值语句定义元件的行为；② 采用“流-势”概念处理不同元件之间的数据交换；③ 良好的符号解析求解能力。

模型采用数学方程而不是赋值语句来定义模型的行为。方程具有陈述式非因果特性，也就是声明方程时没有限定方程的求解方向，因而方程具有比赋值语句更大的灵活性和更强的功能(比如用于处理电生磁、磁生电的问题)。方程可以依据数据环境的需要用于求解不同的变量。这一特性极大地提升了模型的重用性。方程的求解方向最终由仿真求解器根据方程系统的数据流幻境自动确定。这意味着用户不必在建模时将以自然形式表述的方程转化为因果赋值形式，这极大地减轻了建模的工作量，尤其是对于复杂系统建模，同时也可以避免因为公式的转化和推导引起的错误，使模型更加健壮。

模型元件之间的数据交换处理直接关系到整个系统的真实性，模型与模型连接处反映的正是实物部件间的物理联系，必须通过对应领域的物理关系式进行耦合。比较流行的一种做法是采用“流—势”传递的方式进行耦合，即通过控制体进出口流参数之和与控制体内势参数的变化关联起来以达到耦合目的。为了说明这一问题，选取气动领域的连接件进行介绍，如图1所示，3个元件通过连接件(Connection)相互连接，连接件可以看作一个控制体，它会将相邻元件的体积(容性属性)相加作为控制体的体积。通过对应的平衡方程并与热力学第一定律等其他气动热力学公式联立求解控制体内的势参数压力、温度等，并将这些量传递回相连的每个气动元件，参与元件内部的下一步计算。

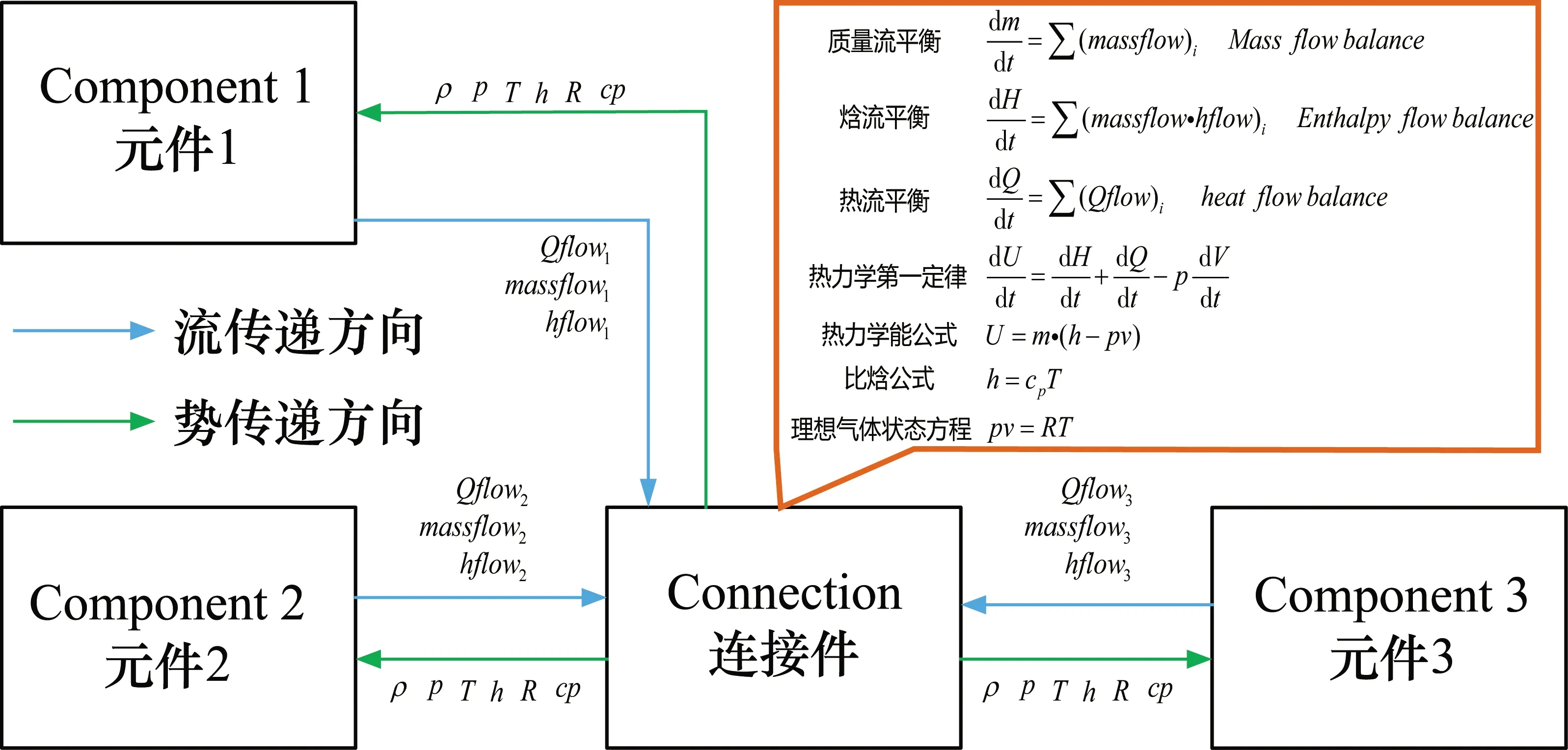
图1 模型元件之间的连接处理示例

对面向对象建模而言，系统模型建立后，需要将模型通过符号转化为雅克比矩阵进行求解，即公式符号运算能力，这其中就会根据边界条件、待求量等模型设置决定模型中公式的具体计算方向。典型的时域仿真计算流程如图2所示，首先对所建模型进行符号分析，将模型转换为可计算的表示形式，并简化方程组、降阶次、确定变量维数等；继而确定方程组最大微分代数阶次；然后确定相容的初始值；最后启动时域仿真，每一个时间步计算完成后，检查是否有事件(比如变量突变、条件激活)发生，如果有则要细化时间步以精确确定该事件的发生时间，停止连续积分，并重新初始化模型，直至仿真结束。

图2 时域仿真计算流程

以上介绍的都是系统仿真中的关键技术，随着多年来的发展，理论体系已经成熟，应运而生了一大批数值求解算法和商业仿真平台。对于针对工作中的物理过程的仿真而言，更应该关注的是系统模型本身对于系统描述的真实性，但了解以上技术细节对于建模、调试仿真至关重要。

2 系统元件建模

自由射流高空台由大量阀门、管道和容腔等元件组成，采用面向对象的建模方法可以方便地使模型重用、组合和拓展，可以按照实际自由射流高空台系统的物理结构构建与实际物理系统相对应的系统与结构。下面分别对各系统元件模型的工作原理和基本方程进行说明。

2.1 可调气动射流喷管

自由射流中的气动射流喷管起着为试验件提供射流来流条件的作用，在对射流喷管建模之前，首先分析其工作原理。喷管在气动上存在3个参考压力P1，P2，P3，喷管进气总压Pt、背压Pb与参考压力的相对大小决定了喷管的7种流态，如图3、式(1)所示。

图3 喷管流态分析

(1)

理论上来说，完全膨胀状态下射流区域内马赫数均匀，并可用式(2)计算：

(2)

然而，自由射流试验的实际工程应用中，由于设备控制精度等问题，并不能采用完全膨胀的射流喷管状态，而一般采用欠膨胀的状态，此时喷管出口存在一个三角形的马赫数均匀区，该区域内马赫数等与喷管出口截面马赫数Ma2一致。试验时一般利用该区域进行来流模拟。根据以上分析，自由射流试验中需要控制的喷管马赫数应该为Ma2而不是Ma1。

需要说明的是，Ma2的计算不能使用完全膨胀状态下的式(2)，而是要根据喷管面积比计算P1，P2，P3等信息，然后结合进排气压力计算。可以理解为，Ma1为气流在进排气压力Pt/Pb环境下经过喷管加速达到的一个平均值，而只有当喷管达到完全膨胀状态时，喷管出口截面上的马赫数才满足Ma2=Ma1(对超音速区而言)。

至此，根据计算所需输入和想获取参数给出了可调气动射流喷管的输入输出，如图4(a)，其中输入参数为：喷管进气总压Pt，喷管进气总温Tt，喉道高度Ht(或半径Rt)，喷管出口高度He(或半径Re)，喷管排气背压Pb。输出参数为：出口可用区气流马赫数Ma2，喷管质量流量Mass。图4(b)中给出了模型的内部计算流程图，其中PortA和PortB即为图1中介绍的模型接口，之间通过容积、流量源来对流过喷管的流量进行约束。

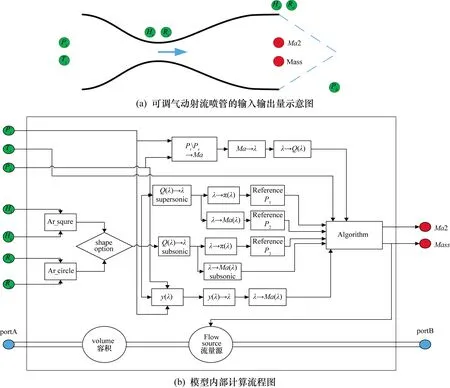
图4 喷管气动模型

为了对以上模型进行验证，对喷管输入进口压力Pt=100 kPa，Tt=20 ℃，出口压力Pb=100～0 kPa的边界条件，同时喷管喉道-出口面积比给定为0.423。如图5所示，模型计算的Ma1、Ma2及通过喷管的流量变化情况均已给出，图5(b)中列出的是进排气压力与喷管面积比所决定的3个参考压力P1，P2，P3的关系，对应喷管所处的不同状态在图5(a)上列出。值得一提的是，喷管的临界压比Pt/Pb并不是0.5283，而是一个与面积比有关的函数。

图5 喷管模型验证

2.2 空气调节阀

空气调节阀通过控制流过空气质量来调节压力，根据文献[4]，气阀的流量计算式如式(3)所示。

(3)

式中，α为阀门流量系数；A2为临界截面积。此二者均为阀门开度(opening)的函数：

α=f1(opening),A2=f2(opening)

(4)

式中，b为临界压比；P2为阀后压力。

A2临界截面积设定为最大开度面积的线性函数。这样，只需要给定流量系数与开度的对应关系就可以确定通过阀门的流量。因为只是进行原理性建模，没有实物测量数据进行模型标定，所以将流量系数给定为一个常数α=constant。

图6给出了最大通流面积为π/4 m2，阀门不同开度(变化范围0～1)下的压比流量特性。

图6 喷管模型压比流量特性

2.3 容积腔体

气动容积效应可以用3个平衡方程来描述，见式(5)。运算时，气动元件将质量流、焓流、热流传入控制体，通过对应的平衡方程并与热力学第一定律等其他气动热力学公式联立求解控制体内的势参数压力温度等。

(5)

补充方程为

U=m·(h-pv)

h=cpT

pv=RT

(6)

2.4 原理性控制系统

控制系统常用反馈控制原理如图7所示，其中控制器常用PI或PID控制器，反馈信号与控制目标值作差经过增益、积分、微分环节输出控制信号以达到控制目的。

图7 反馈控制系统原理

根据自动控制原理，常用的PI控制器输入输出可用式(7)计算，PID控制器输入输出关系可用式(8)表示。

2.1 白藜芦醇对D-半乳糖致衰老小鼠肝脏、脑和心脏等不同组织GCL含量的影响 从表1中可以看出，与正常对照组比较，衰老模型组和白藜芦醇治疗组小鼠肝脏、脑和心脏中的GCL含量均显著降低，差异有统计学意义(P<0.01)。与衰老模型组比较，白藜芦醇治疗组小鼠肝脏、脑和心脏中的GCL含量均显著升高，差异有统计学意义(P<0.01)。

(7)

(8)

转换器负责对信号进行处理，使之符合作动器可接受的信号范围，通常由限值函数与增益函数构成，输入输出关系如式(9)所示。

(9)

对以PI控制为基础的原理性控制模型进行了验证，不考虑系统延时、最大速率等因素，构建如图8所示的控制验证模型，其中阀门1和阀门2共同决定容腔内的压力，设定目标压力为600 kPa，通过调整阀门2的开度对系统进行扰动，阀门1将在控制系统驱使下相应地调整开度以保证容腔内压力恢复为目标压力值。

控制系统给出的阀门1阀位变化、容腔1内的压力变化如图8中红色、蓝色实线所示。可以看出，控制系统能够将控制量稳定在600 kPa，控制作用有效。

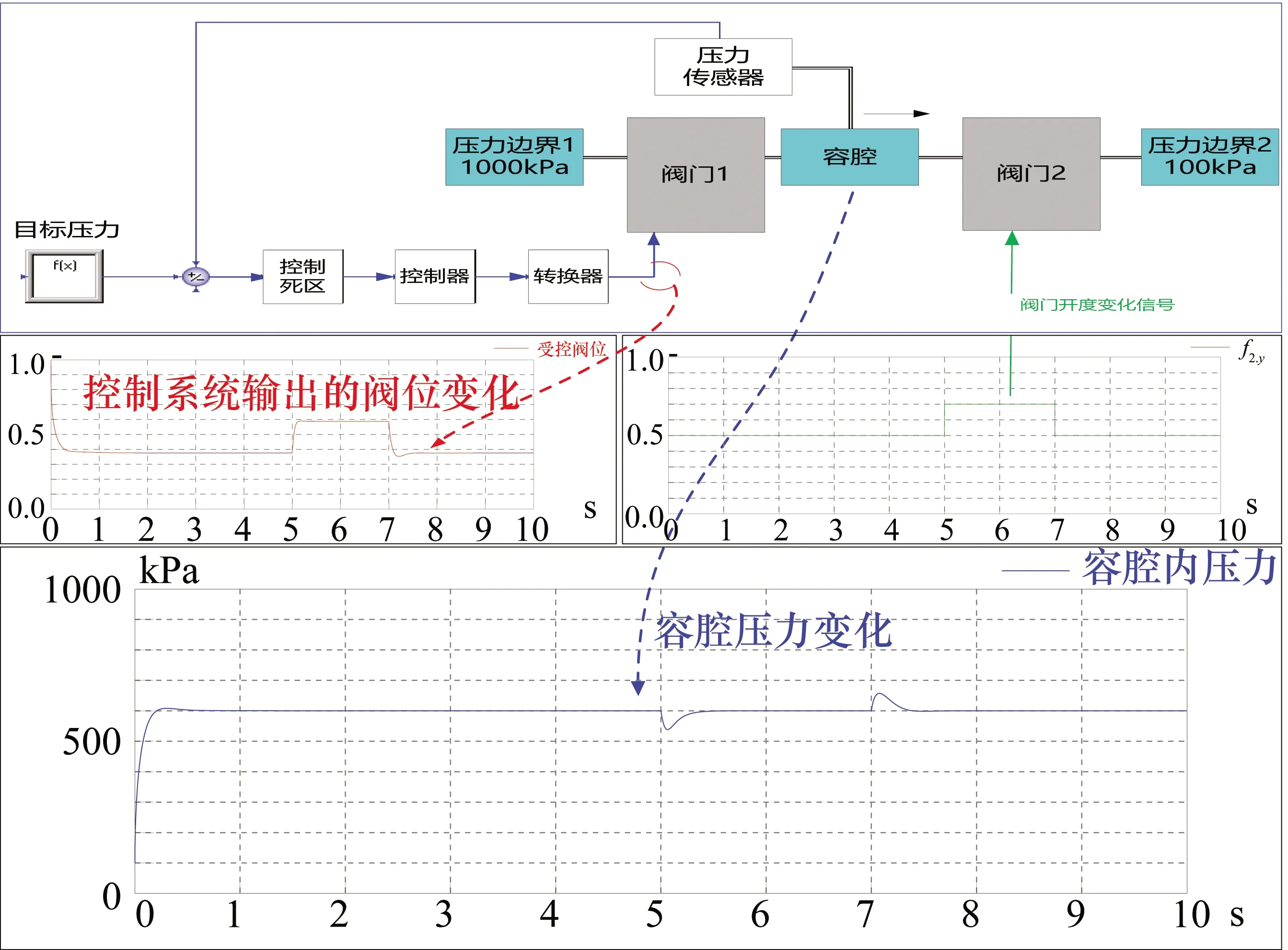
图8 原理性控制系统验证

目前广泛采用的控制方法有PI，PD，PID等，采用PI控制方法兼顾仿真快速性和减小偏差的特点，相比于PID控制器，PI控制系统元件模型易于搭建，能够快速搭建仿真系统的控制模型，采用PI控制可以满足所建系统的控制精度和仿真误差。

3 系统集成及仿真

自由射流高空台系统不同于直连式系统，承担着不同类型的试验任务，为了对自由射流高空台系统进行原理性研究，由大量仿真模型元件构建了相关的空气系统原理模型，图9为简化后的局部模型，主要由供气压力流量边界、排气压力边界、旁路、调压阀、射流喷管构成。

图9 自由射流空气原理局部简化图

以下简化模型旨在研究自由射流试验中的来流、排气环境过渡态模拟问题。

仿真案例1：模拟高度不变，来流马赫数变化。(模拟高度H=8 km，来流马赫数从1.2增加到2.0，再减小到1.5，期间模拟高度不变。)

图10为仿真得到的模拟马赫数、喷管流量变化、前室、排气压力变化情况，以及3个压力调节阀阀位的变化。可以看出，随着模拟马赫数的增大，旁路阀门关小、主流进气阀门开大、排气压力控制阀开大以适应进气流量的增大。

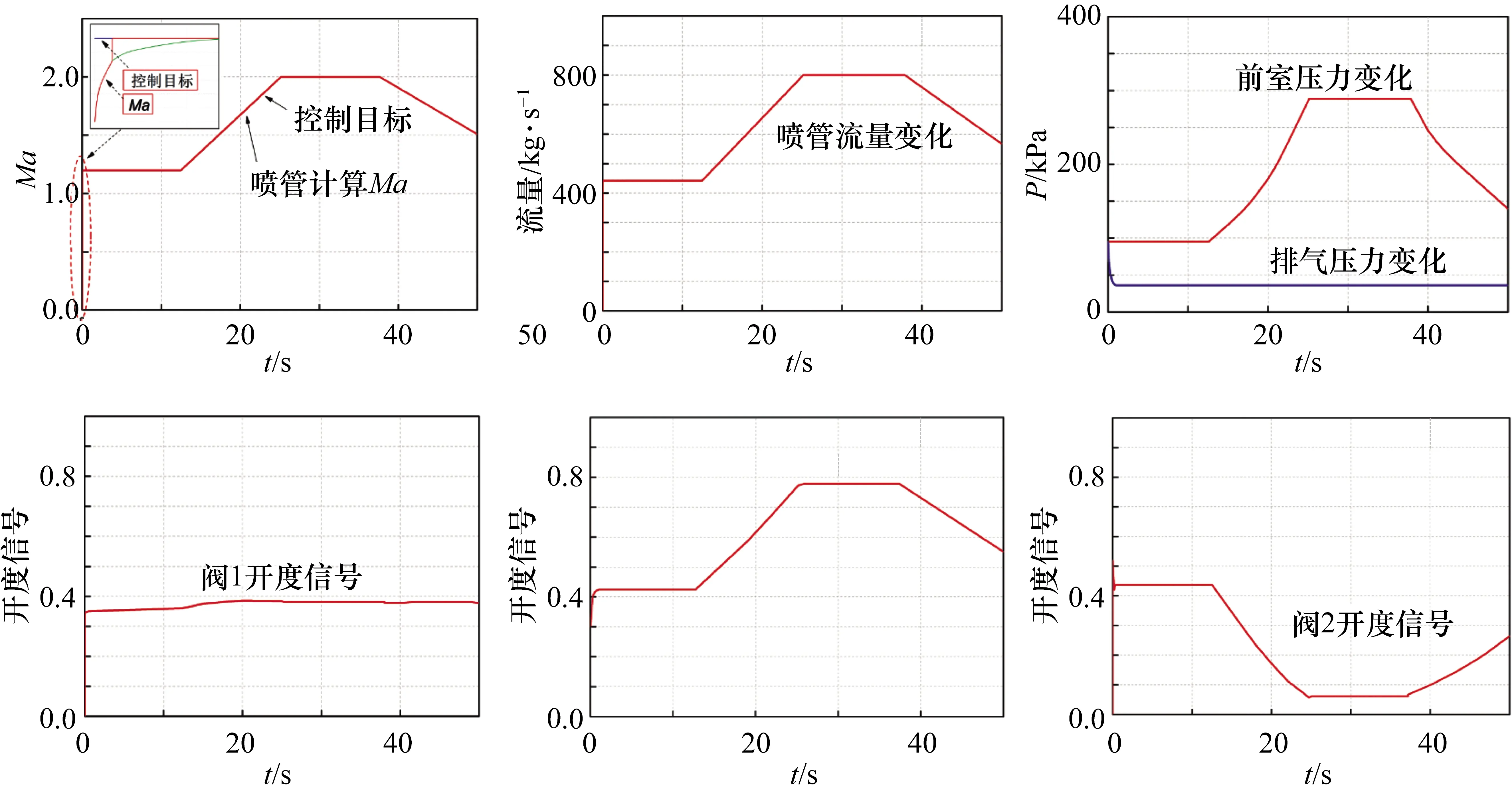
图10 仿真案例1仿真结果

需要说明的是，仿真中采用的控制系统只是原理性的，没有考虑阀门最大变化速率、时间延时等因素，显得控制精度过高，目标马赫数与实测马赫数曲线完全重合了。

仿真案例2：模拟高度变化，来流马赫数变化。(模拟高度从H=8 km增加到H=9.5 km，来流马赫数从1.2增加到2.0，再减小到1.5)。

图11给出了案例2的仿真结果，可见，对于变排气环境的模拟，仿真结果与控制目标之间误差在1 kPa以内。

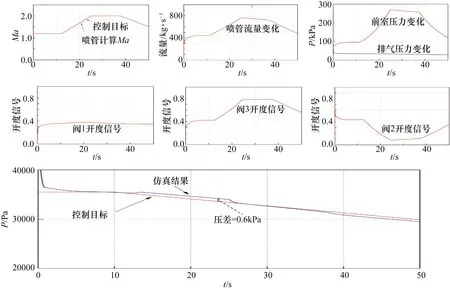
图11 仿真案例2仿真结果

虽然以上模型中控制系统与实际控制系统相比忽略了很多工程因素，但却精确地给出了要实现马赫数瞬态模拟所需要的理论阀门开度变化计划。因此，可以采用以下思路来考虑工程实现，首先由马赫数/高度的模拟计划出发，在经过试验检验的空气系统动态模型基础上，通过高精度动态仿真得到各个阀门的开度计划，然后按计划同步控制各个阀门即可。这样可以避免不同环节控制偏差带来的耦合问题，如图12所示。

图12 各阀门分开同步控制的思路

4 结束语

自由射流高空台系统复杂，各子系统间具有很强的耦合关系。针对复杂系统多领域建模与仿真，目前主要有框图建模(如Simulink)、键合图建模(AMESim)和面向对象建模(Dymola)等建模方式。自由射流高空台由大量阀门、管道和容腔等元件组成，采用面向对象的建模方法可以方便地使模型重用、组合和拓展，可以更加真实地使模型结构接近物理系统结构，通过元件模型可以按照实际自由射流高空台系统的物理结构构建与实际物理系统相对应的系统与结构。

采用面向对象的建模方式对自由射流高空台系统进行了原理性研究，围绕实际的物理对象进行建模，建立了可调气动射流喷管、空气调节阀和容积腔体元件等模型，并针对变马赫数、变模拟高度&变马赫数两种案例进行了计算仿真。元件模型具有通用性和重用性的特点，这两种仿真案例也涵盖了实际试验的典型工作流程，具有代表性。对比了自由射流高空台系统中关键参数压力、开度、流量等目标参数与仿真结果的差异，控制目标参数和仿真结果一致性较好，压力过渡态误差在1 kPa以内，表明仿真方法具有较好仿真精度和技术优势。主要结论如下：

① 所采用技术手段可以用于对复杂系统进行瞬态分析。

② 自由射流试验中喷管模拟马赫数控制应该按本文所列方法计算。

③ 实现自由射流或直连式高空台进排气瞬态控制，原理上是可行的，可以进一步在以下几方面做工作来实现工程实现：各段容腔容积与阀门流通能力的优化、快响应阀门作动系统设计、控制系统的优化等。

使用的面向对象系统仿真技术在分析系统动态特性方面具有巨大的技术优势，然而，数学模型的准确性直接决定结果的正确性，若想在此方面对试验技术起到推动作用，必须未雨绸缪地收集设备特性，摸清设备规律，大量的试验数据和测点是必不可少的，尤其是过渡态数据，对于标定模型尤为重要。该技术的工程实用必须投入相当大的前期建模成本，收集大量的设备资料。