LCL型并网逆变器临界无源阻尼参数设计

陈伟，张岩，屠一鸣，刘进军，姜新生

(1.电力设备电气绝缘国家重点实验室(西安交通大学)，西安市 710049；2.西安中车永电捷通电气有限公司，西安市 710016)

0 引 言

近年来能源危机和环境问题日益严峻，可再生能源分布式发电系统成为研究热点。并网电压源型逆变器被广泛应用于将太阳能、风能等可再生无污染的新能源集成到电网。与传统的L型滤波器相比，LCL型滤波器因其显著的开关谐波衰减能力、低成本和高功率密度，被普遍用于滤波并网逆变器的输出电流。然而，LCL滤波器固有谐振和数字系统控制延迟问题限制了系统控制带宽，提高了电流控制器的设计难度，甚至会影响系统稳定性。

现有的LCL谐振抑制方法主要可分为3类，分别为无源阻尼方法[1]、基于数字滤波器的有源阻尼方法[2]和基于状态变量反馈的有源阻尼控制方法[3-9]。基于数字滤波器的有源阻尼控制方法通过将数字滤波器与电流调节器级联以抑制谐振，该数字滤波器在LCL谐振频率点处存在一个相反的谐振峰来抵消原有的LCL谐振峰，然而实际中需要已知并网逆变器系统的准确参数才能对数字滤波器进行设计，这使得该类方法对系统参数的变化十分敏感。基于状态变量反馈的有源阻尼控制方法通过反馈LCL滤波器的状态变量并选用合适的有源阻尼控制器形成闭环控制来改变被控对象的阻尼特性，达到抑制LCL谐振的目的。这种方法本质上是向谐振网络中加入等效的虚拟阻抗。有源阻尼策略虽然不会给系统增加额外损耗，但反馈量检测传感器会增加系统成本，同时其控制算法复杂，系统可靠性降低。不同于有源阻尼复杂的实现过程，无源阻尼是一种简单可靠的方法，通过在LCL网络中加入阻尼电阻抑制谐振，代价是整机效率降低且高频谐波抑制性能变差[10-14]，但在工程应用中无源阻尼策略仍是最常用的阻尼方法。

通常，如果阻尼电阻选取过小，会引起滤波器谐振抑制不足，影响逆变器电流控制环的稳定性；如果取值过大，会削弱滤波器的高频开关次谐波抑制能力，同时造成更多功率损耗[1]。因此，有必要提出一种精确的阻尼电阻设计标准，在保证系统绝对稳定的前提下尽可能降低损耗。

基于此，本文通过分析控制延时对电网电流单闭环控制系统稳定性的影响，推导系统保持稳定的必要条件；结合阻尼电阻与滤波电容串联和与滤波电容并联两种无源阻尼方法推导分析“临界阻尼系数”指标；根据推导得出的临界阻尼系数值，计算确定阻尼电阻值，并在PLECS软件中进行三相LCL型并网逆变器系统仿真，以验证理论分析的有效性和准确性。

1 LCL型并网逆变器模型

无阻尼情况下，采用电网电流单闭环控制的LCL型并网逆变器系统结构如图1所示。图1中逆变器侧滤波电感L1、网侧滤波电感L2以及滤波电容C共同构成了LCL型滤波器以抑制开关谐波，弱电网线路感抗由Lg表示，同时忽略无源器件的寄生电阻来模拟无阻尼系统。

为简便分析，假定直流侧电压Vdc保持恒定。vinv表示逆变器交流侧输出电压，iL1表示逆变器侧电流，iL2表示网侧电流，iC表示电容电流，vg表示电网电压。

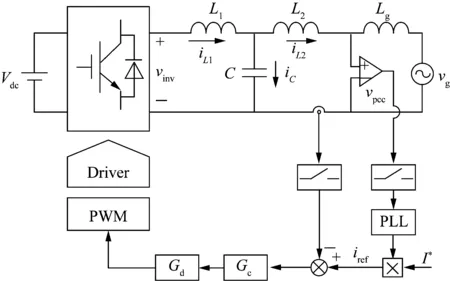
图1 单闭环控制LCL型并网逆变器系统结构Fig.1 System structure of the LCL-type grid-connected inverter with single closed-loop control

公共耦合点电压vpcc的相位通过锁相环得到，从而控制逆变器输出电流与电网电压同步。考虑到由锁相环引起的不稳定通常出现在低频段，在分析LCL高频谐振机理时可忽略其影响。

为实现无静差跟踪交流正弦参考信号，电流调节器Gc(s)采用比例谐振控制器实现，其表达式为：

(1)

式中：Kp为比例系数；Kr为谐振系数；ωg为基波角频率；复变量s相当于时域中的微分算子。

此外，当系统采用规则同步采样策略时，控制延时Gd(s)包括计算延时和脉宽调制延时，由1.5拍采样周期构成，相应表达式为：

Gd(s)=e-1.5Tss

(2)

式中：Ts为采样周期；e为自然常数。

值得强调的是，图1虽表示单相LCL型并网逆变器系统控制结构图，但是当采用abc/αβ坐标变换进行解耦合之后，图1中控制环路仍然适用于三相系统的稳定性分析。

2 电网电流单闭环控制策略

采用电网电流反馈控制策略的LCL型并网逆变器系统控制框图如图2所示。由于电流环开环环路增益可以准确地反映系统稳定性，求取电网电流反馈控制下的环路增益。

根据图2，推导出输出电压vinv(s)到网侧电流iL2(s)的传递函数GLCL(s)，如式(3)所示。

(3)

(4)

式中：ωr表示LCL谐振频率。

图2 LCL型并网逆变器电网电流单闭环控制框图Fig.2 Block diagram of grid current single closed-loop control of LCL-type grid-connected inverter

根据图2，可推导出网侧电流反馈控制的开环环路增益T(s)：

T(s)=Gc(s)KPWMGd(s)GLCL(s)

(5)

式中：KPWM表示逆变器从调制信号到输出电压的增益。忽略电流调节器谐振项对系统高频特性的影响，Gc(s)可近似为Kp。在频域下分析系统频率特性，将s=jω代入式(5)可得环路增益的幅频和相频表达式，如式(6)和式(7)所示。其中ω表示频域里的频率。

(6)

(7)

根据奈奎斯特稳定判据，开环环路增益的右半平面极点个数N等于2(N+-N-)时，系统才可稳定运行。在开环环路增益幅值大于0 dB的频率段内，将相频曲线自下而上穿越(2k+1)π的次数记为N+，自上而下穿越(2k+1)π的次数记为N-。根据式(3)，电网电流反馈控制的环路增益不存在不稳定的极点，即N=0。因此，系统稳定的充分必要条件是N+等于N-。电网电流单闭环控制策略下系统的开环增益波特图如图3所示。可以看出，开环增益的相频曲线不存在正穿越，即N+=0。若想设计一个稳定的系统，T(s)必须满足N-=0。考虑到谐振点ωr处的幅度增益大于0 dB，必须保证T(s)相角在ωr处不穿越(2k+1)π，即：

(8)

求解上述不等式(8)可得fs/6 fs/6时系统也并非绝对稳定，定义临界频率ωcri=2πfs/6。由于在ωcri处相频曲线必定穿越(2k+1)π，需保证ωcri处的环路增益小于1以避免负穿越成立，即不等式|T(ω=ωcri)|<1，求解得式(9)，其对电流控制器比例系数的设计提出了要求。

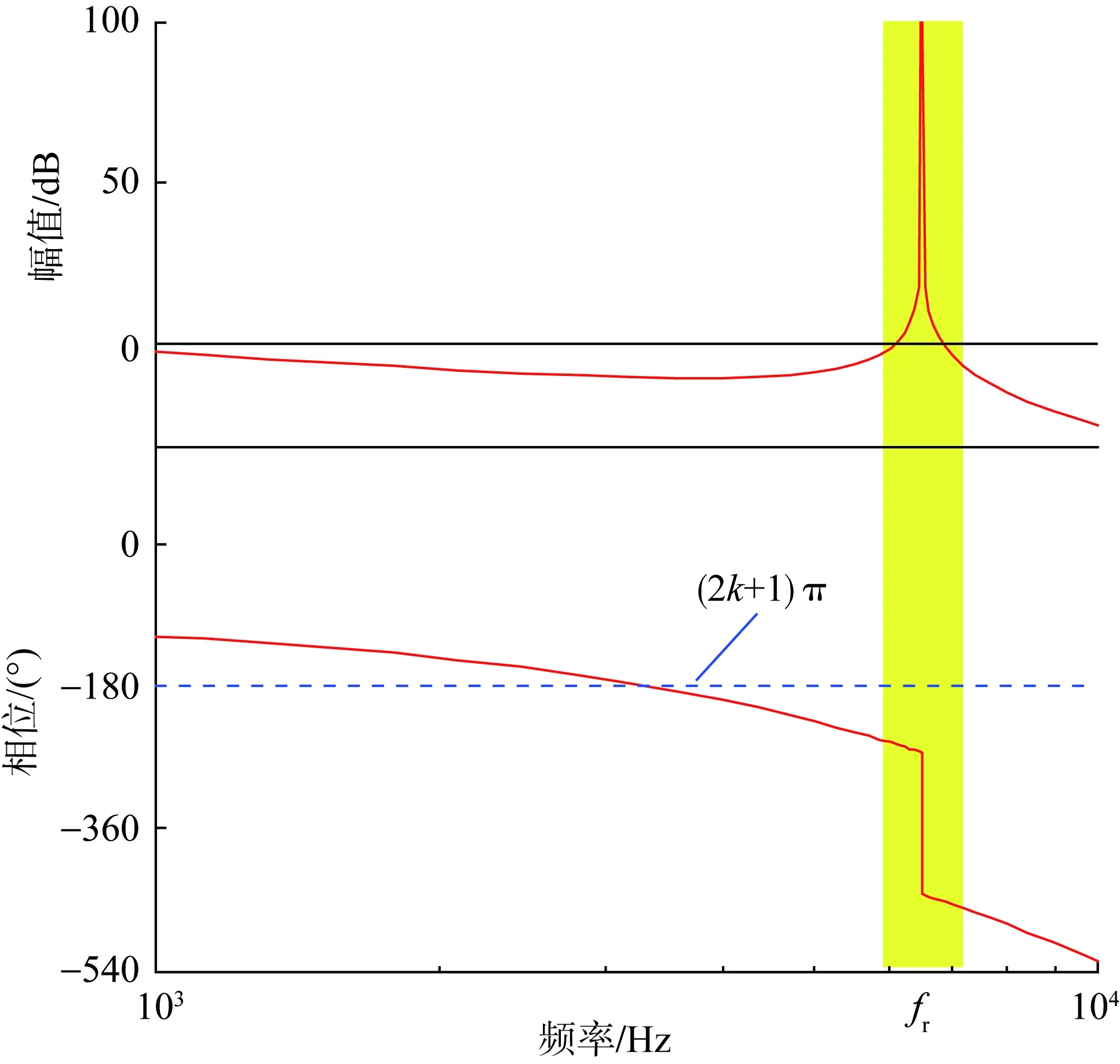
图3 开环增益波特图Fig.3 Bode diagram of open-loop gain

(9)

3 基于临界阻尼比的无源阻尼策略

电网电流单闭环控制虽然可以保持稳定，但谐振峰并没有被消除，因此采用无源阻尼策略很有必要。无源阻尼策略的核心思想是在LCL滤波网络中引入阻尼电阻来吸收高频振荡能量，从而达到抑制LCL谐振的目的。根据阻尼电阻接入LCL滤波网络的不同位置，6种基本的无源阻尼方法如图4所示。图中RD为加入的无源阻尼电阻。

如图4(e)和图4(f)所示，阻尼电阻与滤波电容串联和并联不仅是常用的无源阻尼方法，且对有源阻尼策略等效设计具有参考价值，本文针对这2种无源阻尼策略展开研究。

3.1 电阻与滤波电容串联

滤波电容串联阻尼电阻取值受多种因素影响。一方面为简化设计，RD选取与谐振频率下电容器等效阻抗相同的数量级，推荐值为1/3。然而，采用该原理设计结果可能不精确：如果RD过小，会引起滤波器谐振抑制不足，影响逆变器电流控制环的稳定性；如果RD过大，会削弱滤波器的高频开关谐波抑制能力，同时产生更大的功率损耗。另一方面，阻尼电阻通常是在逆变器侧滤波电感L1、网侧滤波电感L2以及滤波电容C确定后进行设计，而高频电流流过阻尼电阻，致使高频滤波效果与初始设计目标有偏差。因此，需要额外的迭代来调整滤波效果[18-19]，导致设计效率降低和滤波效果不精确。

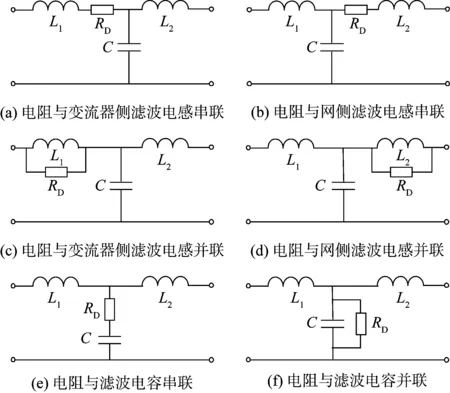
图4 六种无源阻尼方法Fig.4 Six kinds of passive damping methods

因此，本文采用一种临界阻尼的设计思路，使系统开环环路增益T(s)幅频曲线谐振峰达到临界平坦，以最少的阻尼损耗为代价，同时避免失稳。

考虑到电流调节器Gc(s)和控制延时Gd(s)对谐振峰的形状没有影响，因此研究环节GLCL(s)的幅频特性曲线即可反映开环环路增益谐振峰的平坦程度。当电阻与滤波电容串联时，GLCL(s)表达式为：

(10)

为了简化式(10)，结合经典控制理论和表达式(4)，定义阻尼系数ζ如式(11)所示，则GLCL(s)可化简为式(12)。再将s=jω代入式(12)，可得到幅频特性表达式，如(13)所示。

(11)

(12)

(13)

(14)

(15)

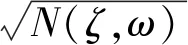
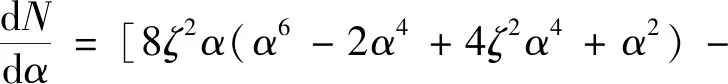
(16)

最终，与谐振峰形状有关的5个变量(L1,L2,C,ω,ζ)被简化为了2个变量(ζ,α)。因此谐振峰与滤波器参数之间的关系可以用二维图形来描述。在不同阻尼系数下，分子多项式num(ζ,α)关于α的函数图像如图5所示。随着阻尼系数ζ增加，满足num(ζ,α)>0的α范围逐渐缩小。当阻尼系数ζ增加到0.28时，num(ζ,α)<0恒成立，这意味着dN/dα<0在全频段内都满足。当ζ>0.28时，GLCL(s)幅频曲线在全频段内单调递减。

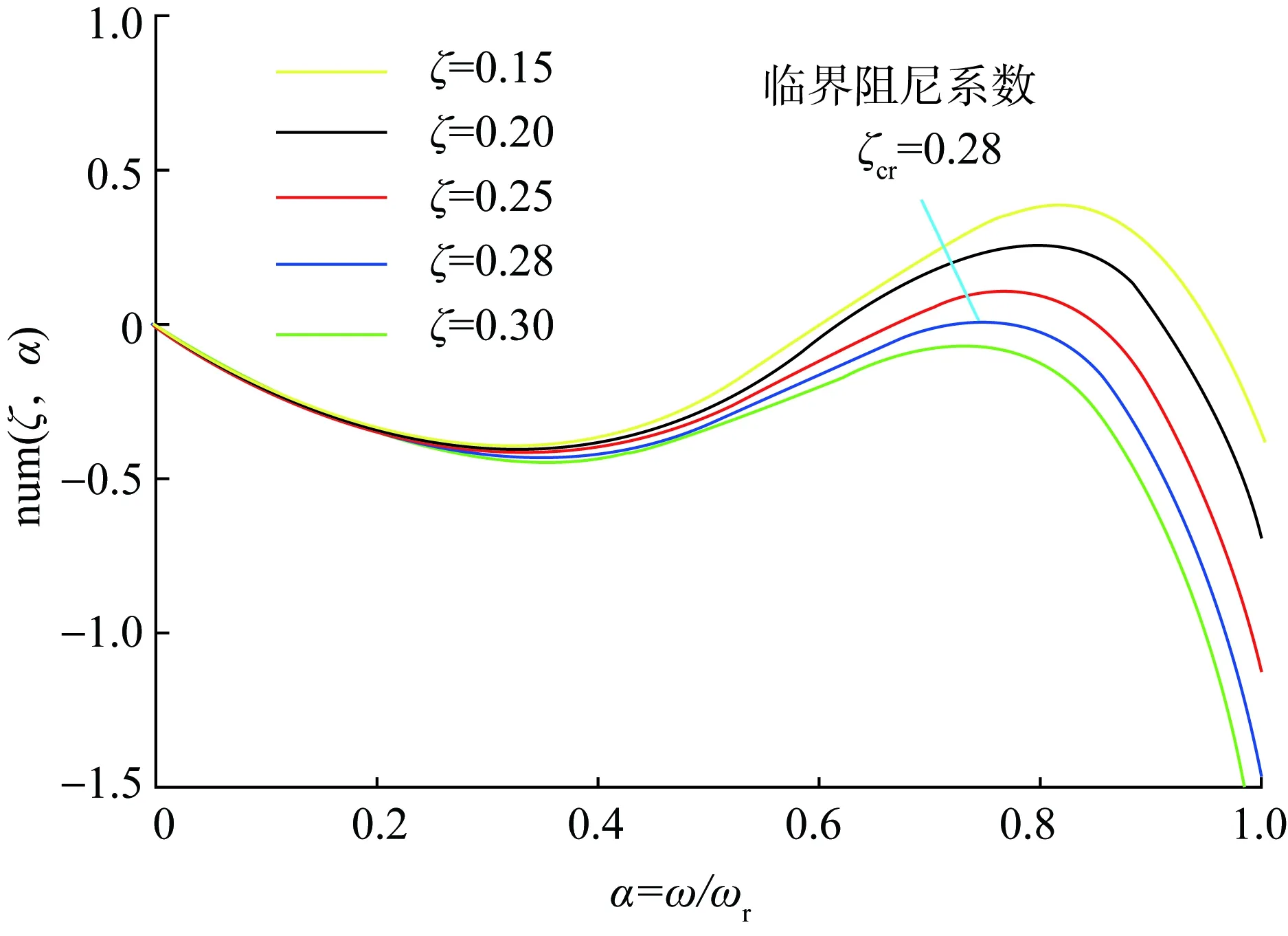
图5 num(ζ ,α)关于α的函数图像Fig.5 Curves of num(ζ,α)against α

综上，定义临界阻尼系数ζcr=0.28可保证系统开环增益谐振峰临界平坦，同时避免非必要的阻尼损耗，如图6所示。考虑到上述推导过程没有引入特定LCL滤波器参数，临界阻尼系数ζcr可以被认为是广义度量指标，适用于电网电流单闭环控制采用电阻与滤波电容串联的无源阻尼策略。

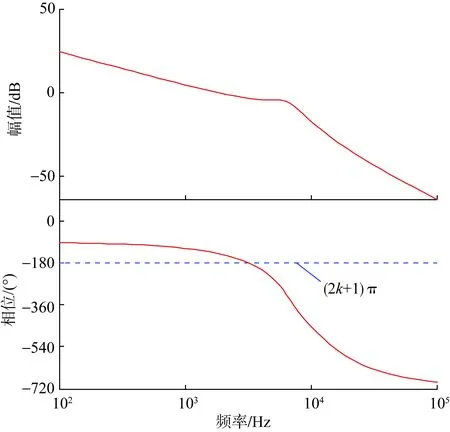
图6 阻尼系数为0.28时电阻与滤波电容串联无源阻尼策略开环增益波特图Fig.6 Open-loop gain Bode diagram of resistor in series with capacitor damping strategy when damping factor is 0.28

3.2 电阻与滤波电容并联

采用同样思路分析电阻与滤波电容并联的无源阻尼方法，只需研究环节GLCL(s)的幅频特性曲线。输出电压vinv(s)到网侧电流iL2(s)传递函数可推导为式(17),定义阻尼比ζ为式(18)，可将GLCL(s)化简为式(19)。

(17)

(18)

(19)

(20)

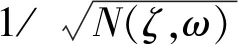
(21)

N(ζ,α)=α2[(1-α2)2+(2ζα)2]

(22)

因此，幅度增益|GLCL(jω)|在整个频率段内单调递减等价于N(ζ,α)单调递增，等价于多项式N(ζ,α)的导数dN/dα在整个频率段内大于或等于0。

(23)

不同阻尼比下，dN/dα关于α的函数图像如图7所示。随着阻尼系数ζ增加，满足dN/dα<0的α范围逐渐缩小。当阻尼系数ζ增加到0.26时，dN/dα>0在所有范围内都成立，这意味着N(ζ,α)在全频段内单调递增。当ζ>0.26时，GLCL(s)幅频曲线在全频段内单调递减，等价于开环环路增益T(s)幅频曲线在全频段内单调递减，相应开环增益波特图如图8所示。综上，电阻与滤波电容并联无源阻尼方法下，临界阻尼系数为0.26。可以看出，对于不同的无源阻尼控制策略，系统的临界阻尼特性也并不相同，因此需要根据所选取的控制方法来设计相匹配的阻尼电阻参数。此外，由于加入阻尼电阻位置的不同而引起的损耗的差异需要单独评估。

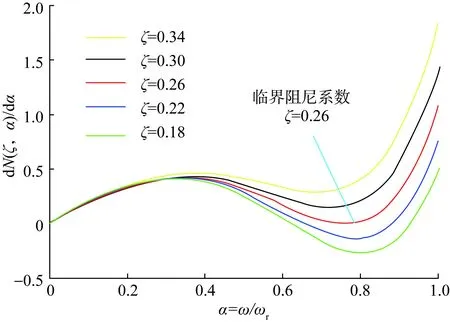
图7 dN(ζ ,α)/dα关于α的函数图像Fig.7 Curves of dN(ζ,α)/dα against α

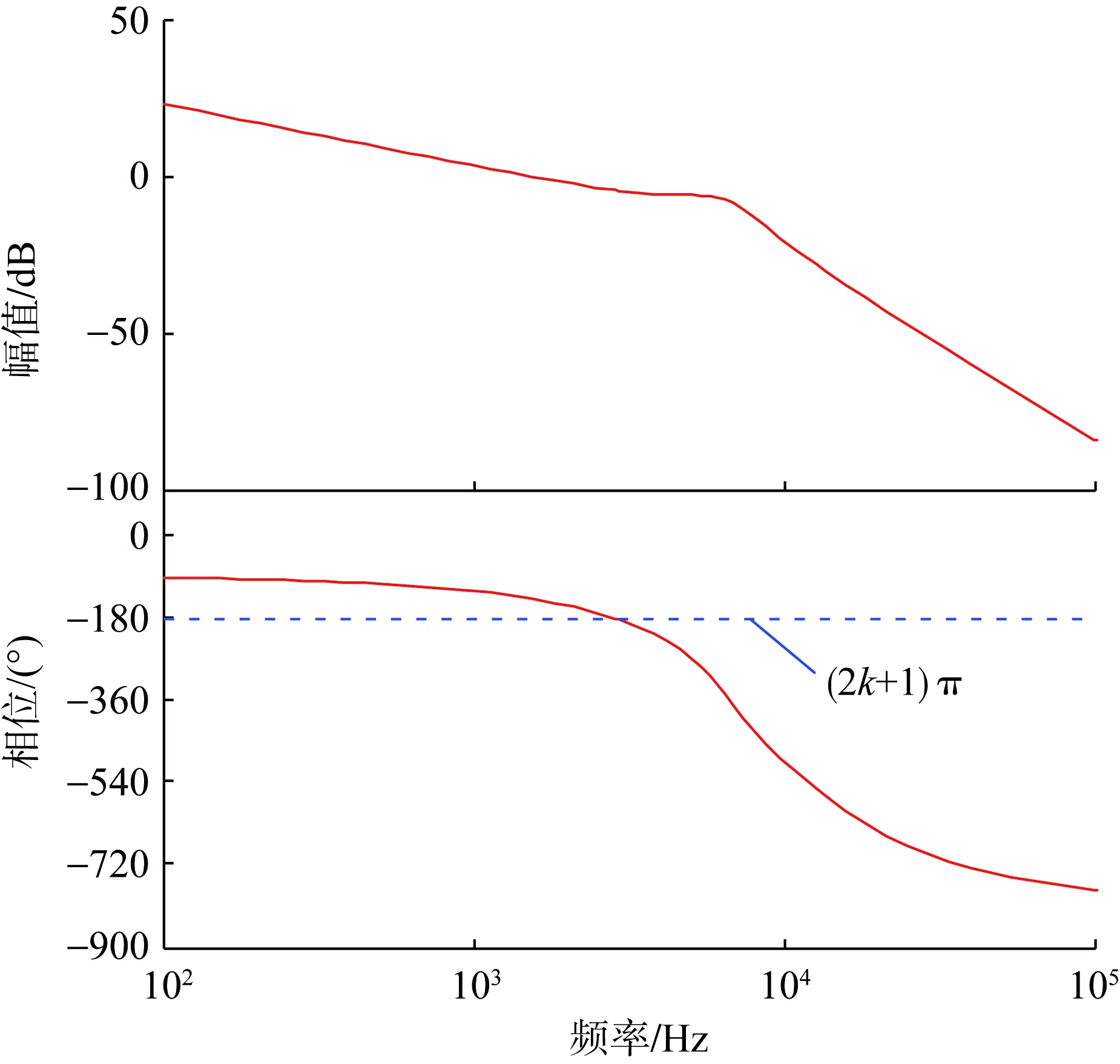
图8 阻尼系数为0.26时电阻与滤波电容并联无源阻尼策略开环增益波特图Fig.8 Open-loop gain Bode diagram of resistor in parallel with capacitor damping strategy when damping factor is 0.26

4 仿真验证

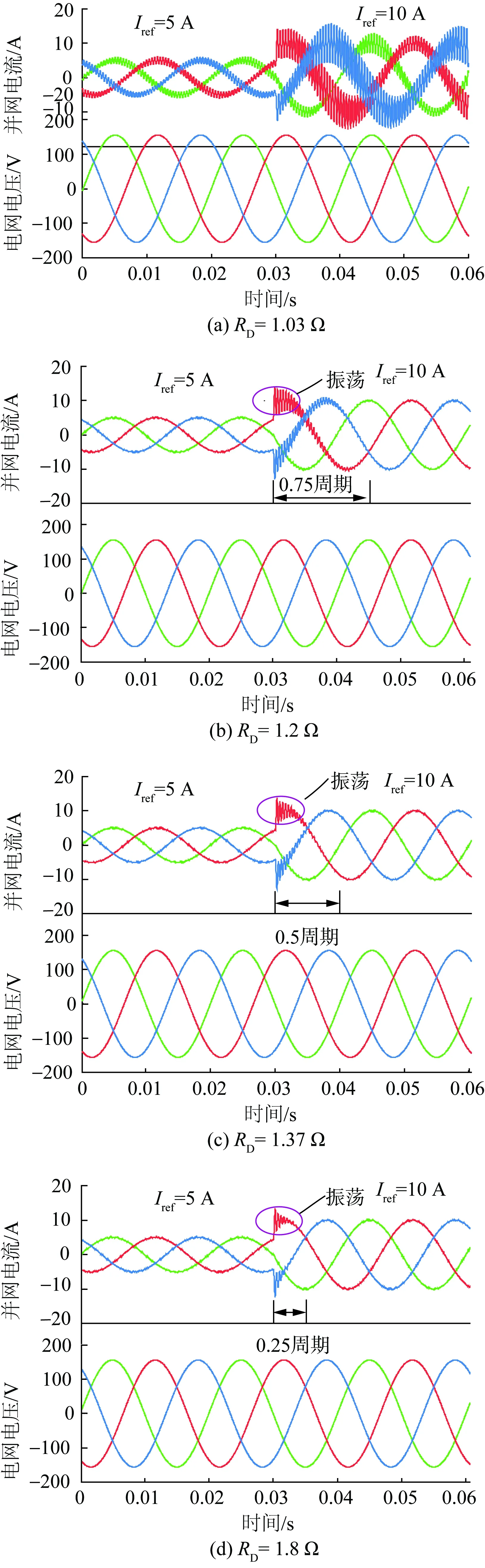
为验证本文提出的临界阻尼设计方法对LCL三阶滤波器高频谐振的抑制效果，以及相应工况下的稳定性，在PLECS软件中进行三相并网逆变器系统仿真，具体仿真参数如表1 所示。采用电网电流单闭环控制时，由于谐振频率fr

表1 三相并网逆变器系统仿真参数Table 1 Simulation parameters of three-phase grid-connected inverter system

除了临界阻尼电阻之外，本文还设置3组其他电阻取值进行仿真对比，分别为1.03、1.20、1.80 Ω，相应的三相并网电流和电压仿真波形如图9所示。为分析系统动态性能，在0.03 s时电流指令参考值发生5 A到10 A的阶跃变化。从图9(a)可以看出，当电阻取值较小时，系统阻尼不足，稳态运行和瞬态阶跃过程都难以保持稳定，并网电流发生严重高频振荡，影响逆变器安全运行，甚至会引起一系列的大规模振荡事故，危及大电网的稳定性。此外，这也证明了当谐振频率低于1/6采样频率时，仅采用网侧电流单闭环控制无法使系统保持稳定。

对比图9(b)—(d)可以看出，随着阻尼电阻数值增加，系统的稳定性增强，且阶跃响应调节时间明显减小，分别为0.75、0.50和0.25个周期。但是，阻尼电阻的增加是以更多的功率损耗为代价，因此需要在系统动态性能、稳定性和效率三者之间折衷选取。

从图9(c)临界无源阻尼方法下的并网电流仿真波形可以看出，在指令值从5 A 阶跃到10 A 时，并网电流可以快速跟踪指令值，动态性能较好，整个系统保持稳定，高频谐振问题得到抑制，且并网电流谐波含量低，验证了本文提出的临界阻尼电阻设计的准确性和优越性。需要指出的是，图4中的6种无源阻尼方法均可以采用此方法进行分析，且结论应与图9的仿真结果吻合，不再进行重复讨论。

图9 不同阻尼电阻与滤波电容串联时并网电流和电压仿真波形Fig.9 Simulation waveforms of grid-connected current and voltage when different damping resistors are connected in series with filter capacitors

5 结 论

传统的LCL滤波器设计方法主要缺点是阻尼参数的设计原则是非最优的，这意味着开环幅频特性曲线上的谐振峰可能无法得到完全抑制，造成180°穿越引发系统不稳定。为了解决这个问题，本文引入阻尼系数作为中间变量，简化了谐振峰与滤波器参数之间的数学关系，并通过二维图形来描述这一关系，求解出临界阻尼系数，保证了幅频特性曲线上的谐振峰临界单调递减，避免引入不必要的阻尼损耗，同时充分抑制了LCL滤波器谐振，简化了阻尼电阻的设计过程，对实际的工程应用，具有一定参考价值。

然而，无源阻尼控制总是会伴随着额外的损耗，将来的研究可以考虑将临界阻尼系数的概念引入到有源阻尼控制策略中，以指导有源阻尼控制参数的设计与整定。