风电场交直流并网次/超同步振荡交互影响

杨秀,胡浩然，李增尧，李莉华，吴琼，徐立成

(1.上海电力大学电气工程学院，上海市200090；2.国网上海市电力公司电力科学研究院，上海市200092；3.中国长江电力股份有限公司，湖北省宜昌市443002)

0 引 言

面对化石能源枯竭、环境污染和气候变暖等问题，大规模开发利用风电等可再生能源，实现全球能源变革转型，是应对当前能源问题的必由之路。其中，风能已经成为发展最快的能源，近年来随着风电装机容量的不断增加，柔性直流 (voltage source converter based high voltage direct current,VSC-HVDC)输电以其线路损耗小、控制简单快捷、不会发生换相失败等优势成为风电远距离输送的有效方式[1]。因此，以交直流混联为特征的输电方式成为风电大规模输送的常见形式。同时，由于复杂的控制策略，柔性直流系统的接入给抑制风电新型次/超同步振荡带来了新的挑战[2]。

自21世纪以来，风电工程中次同步振荡问题的屡次出现引发了学者的广泛关注。2012年河北沽源地区以及2009年美国德州的双馈风机(double-fed induction generator，DFIG)经串补送出工程中发生了5～10 Hz以及22 Hz左右的次同步振荡现象[3]；2015年新疆哈密地区直驱风电场经交流送出工程中发生过一起20～90 Hz之间的多频段次/超同步振荡现象，并引起附近火电机组保护切机[3-4]；广东南澳双馈风电场经柔性直流送出工程发生过30 Hz左右的次同步振荡现象[5]。上海南汇风电场经柔性直流送出工程、福建厦门风电场经柔性直流送出工程发生过相应的次同步振荡现象[6]。因此，风电场无论是经交流系统还是经直流系统送出都存在次同步振荡风险，本文研究的内容具有较大的实际工程意义。

目前，国内外对风电场次同步振荡已经进行了大量的研究，主要针对风电场经柔性直流或者风电场经交流等单一类型的机理分析，对于不同风机类型以及不同输电方式并联的研究较少，缺少对系统结构参数的研究。同时对于交直流两种不同方式下的互相影响更是鲜有研究。在设计控制器参数时，通常在风电场单独经过交直输电系统情况下进行设计，从而忽略了交直流系统之间耦合振荡模式的影响。文献[7]在设计阻尼控制器时仅考虑了风机单独经过交直流的情况，对交直流系统之间的耦合振荡模式欠考虑。文献[8-12]的风机研究对象均为单一的风机类型，而真实的风电工程中存在不同类型的风机，单一类型的风电场并不能体现真实情况；文献[13-18]均是将风电场等值聚合成一台单机风电场接入电网，但缺少系统结构参数对耦合振荡影响的研究；文献[19-22]均是风电场经过柔性直流或者交流单独接入电网，并没有考虑不同接入方式下风电场以及交直流输电方式之间的交互影响。明确不同方式引发的交互影响有利于针对性地设计其抑制措施，从而能够更加准确、经济地减少次同步振荡对电网带来的影响。因此，文中重点关注不同风电场经交直流两种不同接入方式并网之间产生的交互影响，以及系统参数对耦合振荡模式与固有振荡模式影响的差异性。

文中首先建立多风机经交直流接入方式下系统的状态空间模型。利用特征值分析法对所建立的状态空间模型进行分析，并对系统引发的次/超同步现象和振荡机理进行深入研究。然后通过在PSCAD/EMTDC平台进行时域仿真验证所建立状态空间模型的正确性。进一步地，通过改变系统结构参数与控制器参数研究系统参数对固有振荡模式与耦合振荡模式影响的差异性。最后通过对比分析研究交直流并网系统之间的交互影响。

1 风电场经交直流并网系统的动态模型

文中建立风电场经交直流并网系统的拓扑如图1所示。系统主要包含直流与交流两部分，其中直流部分为永磁直驱风机(direct-drive permanent magnet synchronous generator，D-PMSG)经柔性直流线路并网，交流部分为双馈风机经交流线路并网。文献[23]表明，风电机组单机模型与多机模型的振荡规律几乎一致，因此以等值聚合的D-PMSG模拟直驱风电场；以等值聚合的DFIG模拟双馈风电场。永磁直驱风电场经交流输电线路与变压器升压后连接VSC-HVDC系统；双馈风电场经交流线路与直驱风机经VSC-HVDC系统相连一起输送到受端电网；永磁风机与双馈风机的轴系均与发电机直接相连；除发电机的机侧控制器采用基于转子磁链定向的空间矢量控制策略外，其余控制器均采用基于电网电压的空间矢量控制策略。

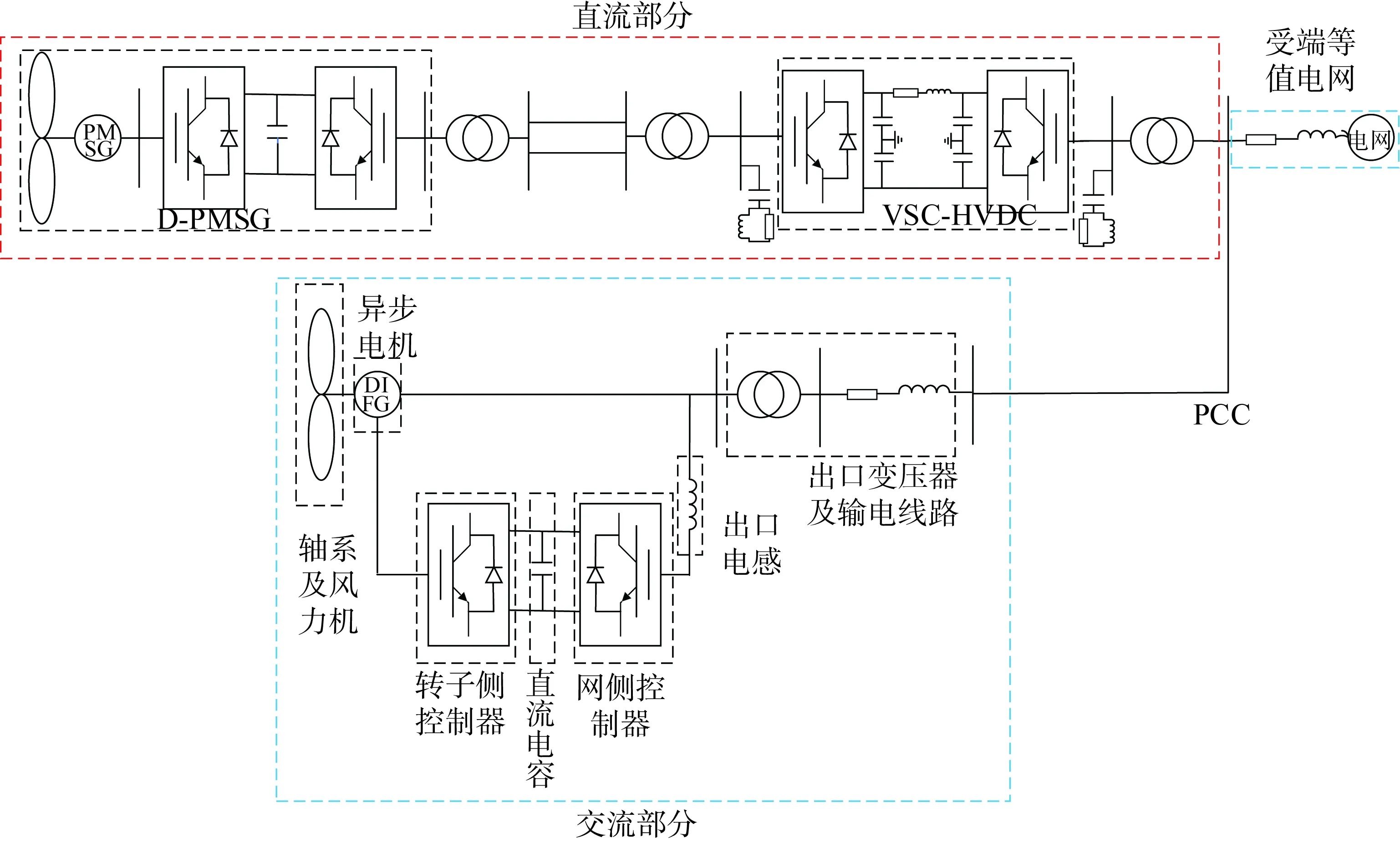
图1 风电场经交直流并网系统拓扑图Fig.1 Topology diagram of wind power grid-connected system through AC and DC lines

1.1 双馈风机的动态模型

双馈风机动态模型主要包括轴系与风力机、发电机、锁相环、转子侧与网侧控制器及其控制系统。

1)轴系与风力机。

文献[23]指出随着质量块数目的增加，模型的精度也在提高。因此，在双馈风机建模中采用双质量模块比采用单质量模块更能详细描述DFIG的轴系机械特性。双质量模块的轴系线性化模型为：

(1)

式中：p=d/dt，为微分算子；TJ1、TJ2、Δω1、Δω2分别为风力机与发电机转子的惯性时间常数与电气转速；ωb为基准的电气转速；D12、D11、D22为风力机与发电机之间的互阻尼系数与自阻尼系数；K12为轴系的刚度系数；Δδ1、Δδ2分别为风力机和发电机转子相对于额定电气转速同步旋转参考轴的电气角位移；ΔT1、ΔT2分别为风机机械转矩、电磁转矩。

2)发电机与直流侧电容器。

异步感应电机的动态模型由电压方程和磁链方程组成，其在正序旋转坐标系下的动态方程为：

(2)

(3)

式中:uds、uqs、udr、uqr、ids、iqs、idr、iqr分别为双馈风机定、转子电压和电流的d、q轴分量；Ψds、Ψqs、Ψdr、Ψqr分别为双馈风机定、转子d、q轴磁链；Rs、Rr分别为定、转子电阻；ωs为同步角速度；Xm、Xs、Xr分别为励磁绕组与定、转子电抗；s为转差。

直流环节变频器两端功率平衡方程为：

CdcUdcpUdc=udgidg+uqgiqg-(udridr+uqriqr)

(4)

式中：Cdc为直流电容；Udc为背靠背换流器的直流电压；udg、uqg为网侧d、q轴电压；idg、iqg为网侧d、q轴电流。

3)转子侧与网侧控制器及其控制系统。

转子侧换流器的控制目标主要是为了维持发电机的输出有功功率在想要的范围内并且使发电机的机端电压保持稳定。转子侧变换器控制系统由外环功率控制和内环转子电流控制组成，并将其d轴固定在转子磁链上，其解耦的控制框图及动态模型分别如图2和式(5)所示。

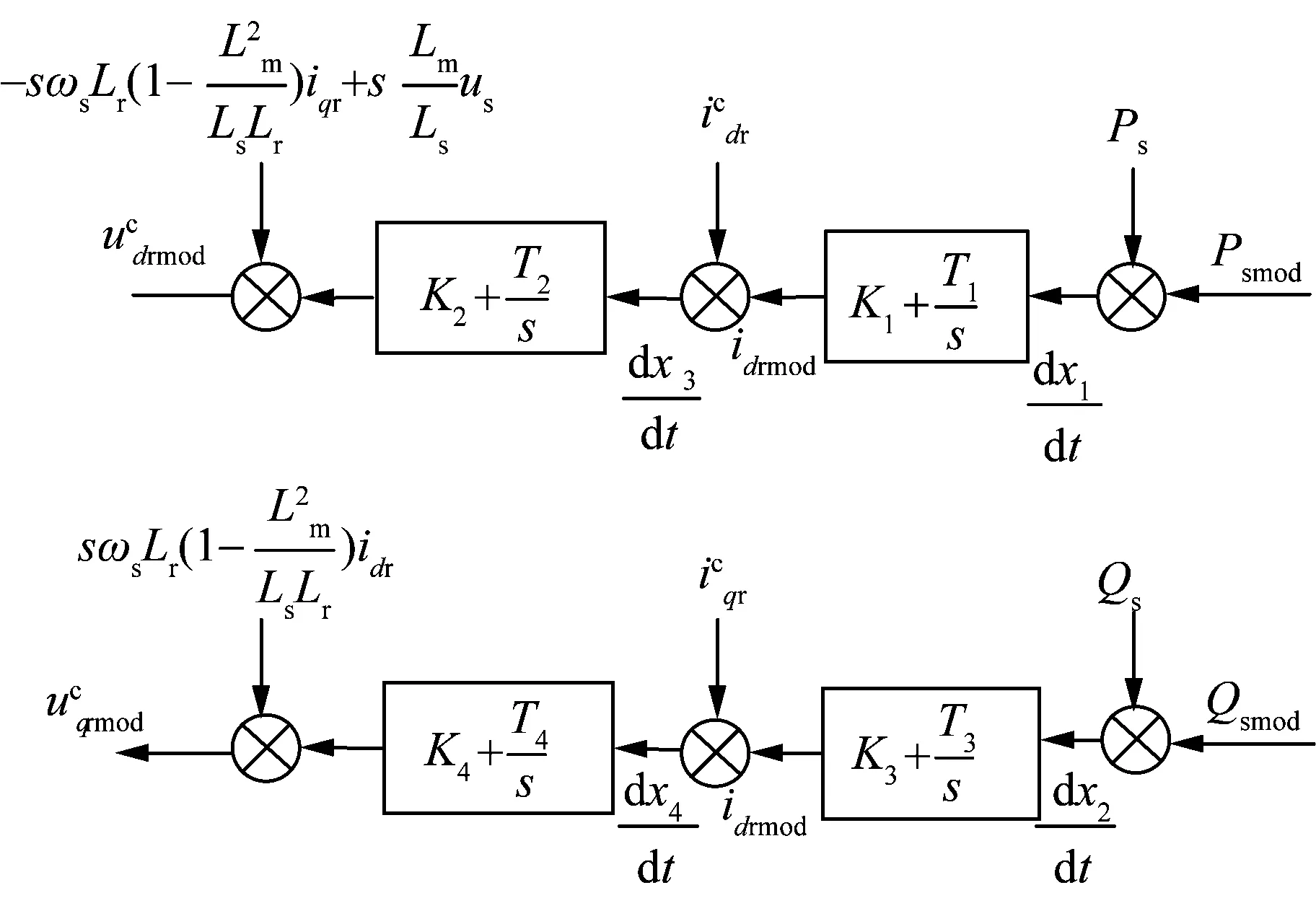
图2 转子侧控制器控制图Fig.2 Block diagram of the rotor-side controller

(5)

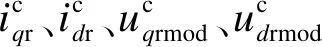
网侧变换器的控制目的是对交流侧的单位功率因数进行控制以及对直流环节的电压稳定性进行控制，网侧换流器也可对电网提供适当的无功功率支持。其是由内环网侧电流控制器和外环电压控制器组成的双闭环结构，解耦的控制框图及动态模型分别如图3和式(6)所示。

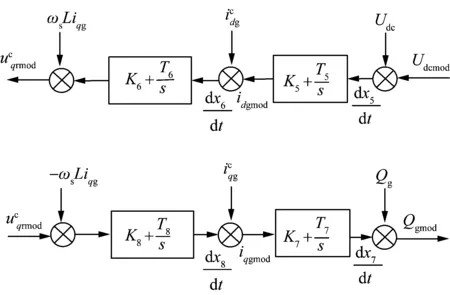
图3 网侧换流器控制图Fig.3 Block diagram of grid-side converter

(6)

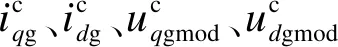
4)锁相环。

PLL的主要功能是“锁定”输入信号的相位，PLL的输出相位用于风电并网系统换流控制器中的派克变换。锁相环模型控制框图与动态模型分别如图4和式(7)所示。

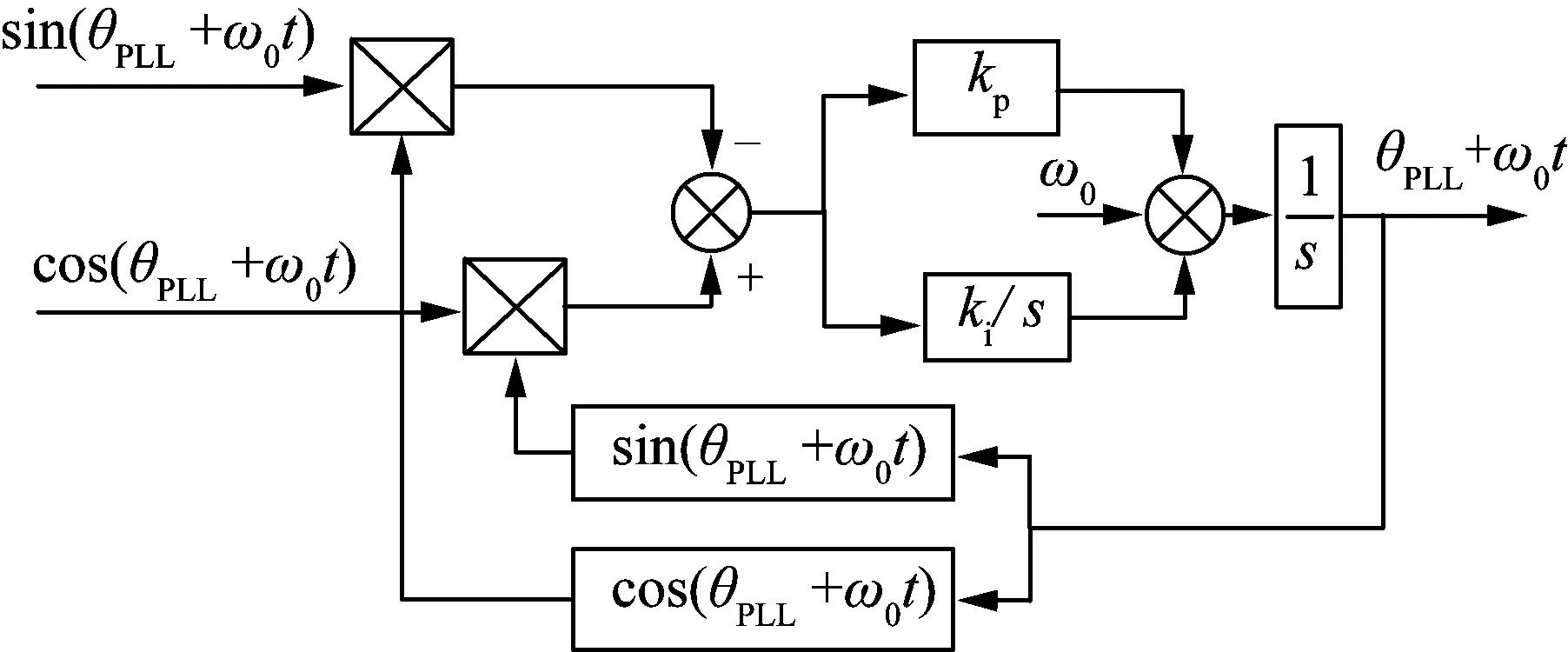
图4 锁相环模型Fig.4 PLL model

(7)

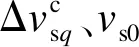
5)交流网络。

交流网络的动态模型为：

(8)

式中：Δucd、Δucq、Δusd、Δusq分别为线路末端、线路首端电压的d、q轴分量；ωs1b、ωs10分别为电网基准角频率、受到扰动时电网频率；R1、L1分别为线路电阻、电抗；Δisd、Δisq分别为线路电流d、q轴分量。

1.2 直驱风机与柔性直流动态模型

直驱风机动态模型与双馈风机动态模型模块内容相似，这里不再赘述。限于篇幅，直驱风机与柔性直流动态模型及其控制框图见文献[24-25]。

1.3 接口方程与坐标变换

在建立统一状态空间模型时，常常会出现各模块的基准坐标系不同的现象，因此需要利用锁相环与坐标变换将各模块坐标系统一。文中在建立永磁直驱风机换流器模型与交流环节、柔性直流受端换流器与交流环节、双馈风机网侧换流器与交流环节所用的坐标系均不在同一坐标系下。

假设两个正序同步旋转坐标系之间的夹角为θ，则它们之间的坐标变换关系如图5所示。

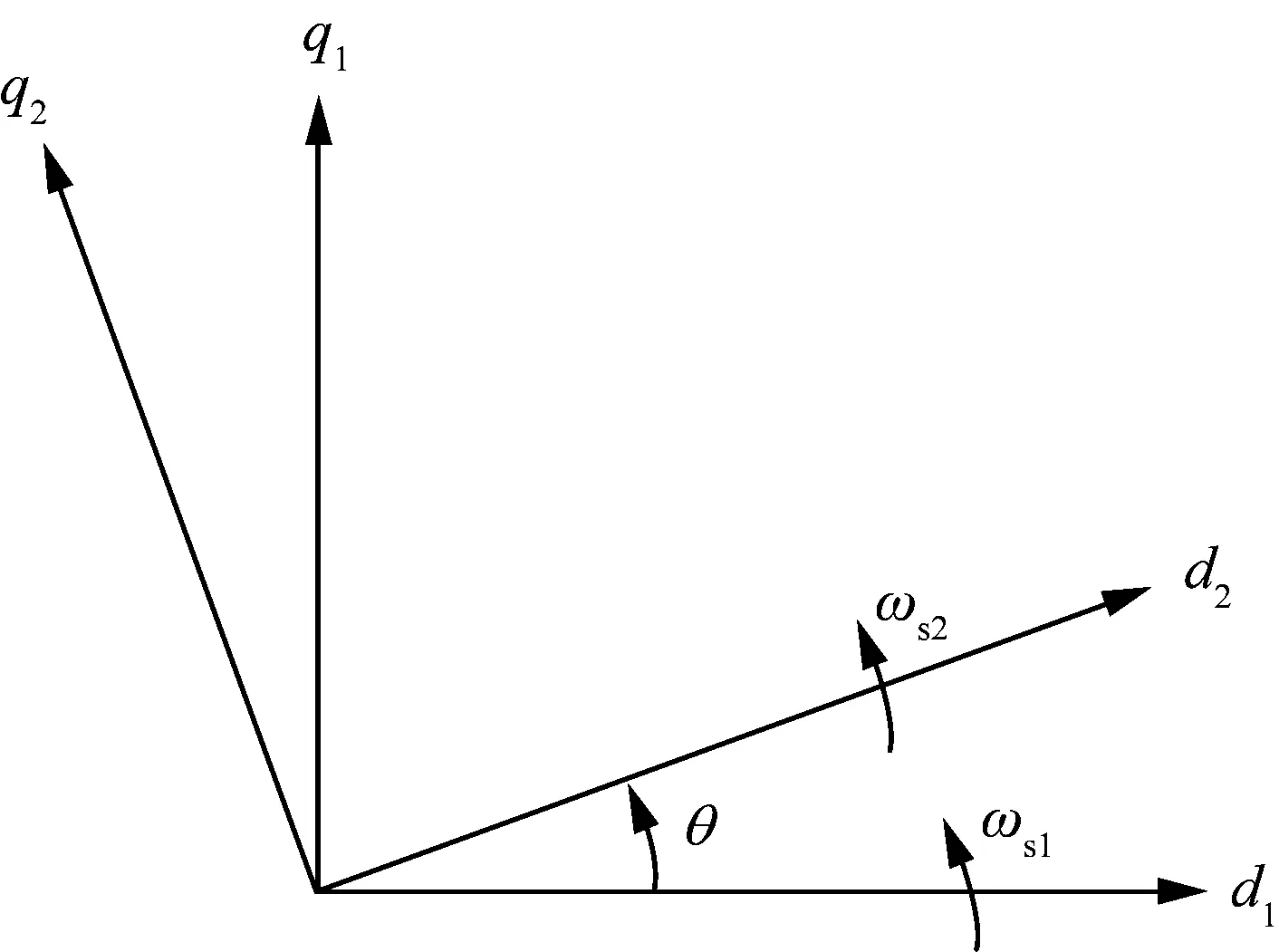
图5 不同坐标系下变换关系图Fig.5 Diagram of transformation relationship in different coordinate systems

两坐标系之间的转换方程如式(9)所示：

(9)

式中：Δfd1、Δfq1、Δfd2、Δfq2分别为坐标系d1-q1、坐标系d2-q2的d、q轴分量。

以永磁直驱风机换流器模型与交流环节为例：

(10)

式中：XI为接口的状态变量；XG为永磁直驱风机的状态变量；XL为交流环节的状态变量；YGL为永磁直驱风机模型与交流环节的代数变量；AG、AL、BGL分别为永磁直驱风机、交流环节、接口方程的系数矩阵。

1.4 全系统状态空间模型

将上述各个模型的数学方程通过线性化可得各模块的状态空间模型为：

(11)

式中：X、Y、A1、B1、C1分别代表状态变量、系统代数变量、状态矩阵、状态变量与代数变量之间的关系矩阵、代数变量与状态变量之间的关系矩阵。

通过各个模块之间的输入输出关系，结合坐标变换可将整体模块整合为同一坐标系下整体状态空间模型。

(12)

全系统状态空间模型详见附录A式(A1)。

2 风电场经交直流并网系统机理分析

2.1 特征值及参与因子计算

系统初始条件：风速设为12 m/s；桨距角设为0；机侧控制器(machine-side controller,MSC)的d轴参考电流设置为0；网侧控制器(grid-side controller,GSC)的无功功率参考值设为0.06 pu；直流电压参考值设为1.0 pu；送端控制器(sending-end controller,SEC)的有功功率参考值设为0.28 pu；无功功率参考值设为0.10 pu；受端控制器(receiving-end controller,REC)的无功功率参考值设为0.02 pu；直流电压参考值设为1.0 pu；直流输电距离为100 km；受端短路比(short cirucit ratio,SCR)为4。风机容量为200 MW；风机与VSC-HVDC具体参数见附录表A1—A3。基于1.3节状态空间模型在以上初始运行条件下得到的特征值分析结果如表1所示。

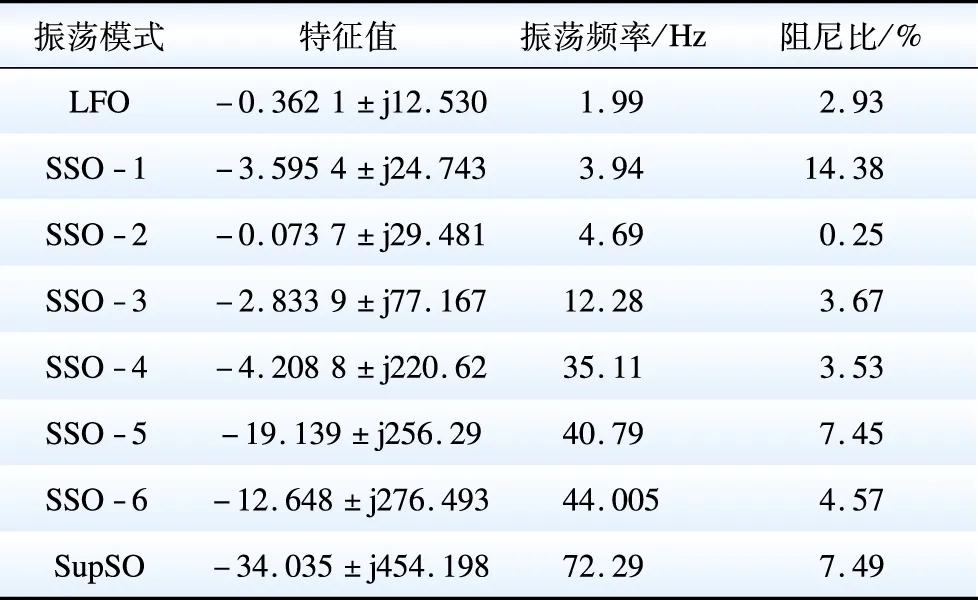
表1 特征值计算结果Table 1 Eigenvalue calculation result

LFO振荡模式的阻尼比为2.93%，小于其稳定所需的阻尼比阈值5%；在次同步频段内，SSO-1、SSO-2、SSO-3、SSO-4、SSO-5、SSO-6模式的阻尼比分别为14.38%、0.25%、3.67%、3.53%、7.45%、4.57%。可见，除SSO-2外阻尼比较高，因此较为稳定；SupSO振荡模式的阻尼比为7.49%，具备一定的稳定性。

因此，最易失稳的振荡模式是LFO、SSO-2模式。进一步分析各振荡模式的参与因子如表2所示。表2中：Δx1、Δx3分别为双馈风机机侧外环有功功率、内环d轴电流状态变量；Δx7为双馈风机网侧内环d轴电流状态变量；Δx9、Δx10分别为永磁风机网侧电压d轴状态变量、电流控制器d轴状态变量；Δω4为永磁风机风力机转子的电气转速；Δδ4为风力机转子相对于额定电气转速同步旋转参考轴的电气角位移；Δudc为风机直流电容端电压；Δw1、Δw3分别为永磁风机机侧电流控制器d、q轴状态变量；Δy1、Δy3分别为VSC-HVDC送端外环有功无功控制器d、q轴状态变量；Δy4为送端内环电流控制器d轴状态变量；Δz2、Δz4分别为VSC-HVDC受端内环电流控制器d、q轴状态变量；Δiq为永磁直驱风机并网电流q轴状态变量；Δisd、Δisq、分别为D-PMSG与VSC-HVDC之间交流网络电流分量d、q轴状态变量；Δis1d、Δis1q分别为VSC-HVDC受端交流网络电流分量d、q轴状态变量；Δis2d、Δis2q分别为DFIG外送交流网络电流分量d、q轴状态变量；Δis3d、Δis3q分别为VSC-HVDC送端出口电流与DFIG交流线路电流之和d、q轴状态变量。

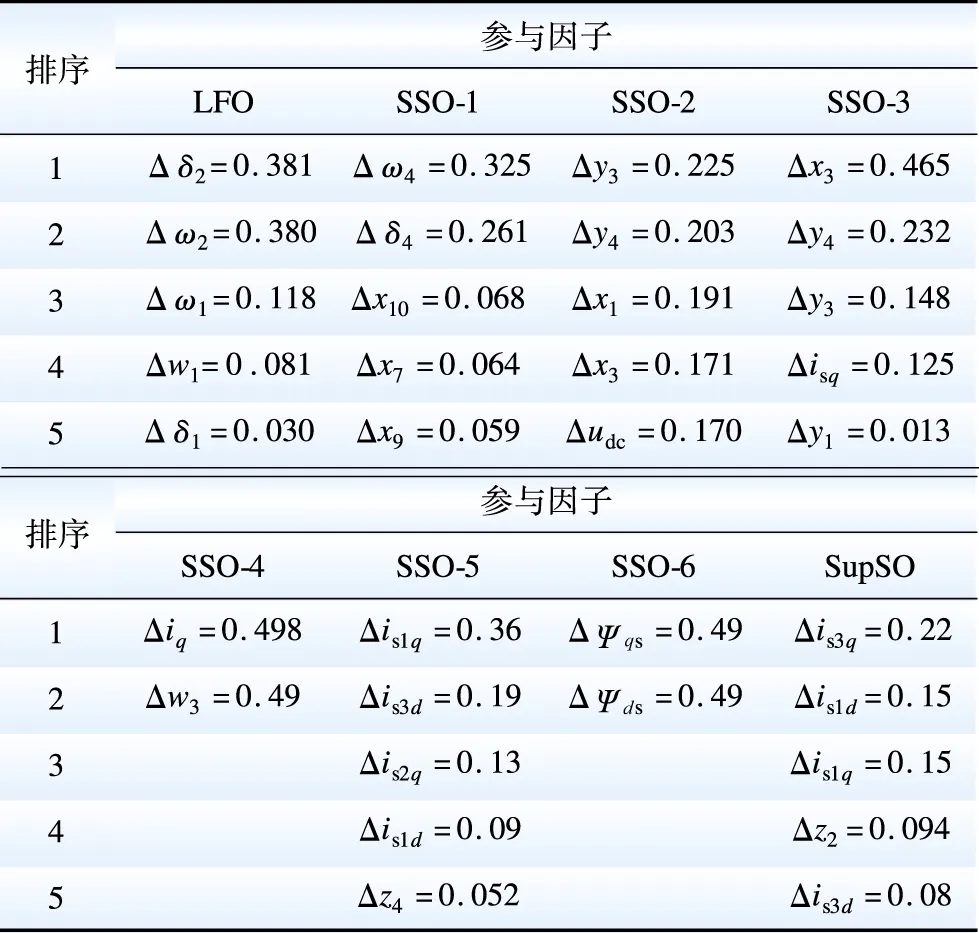
表2 各振荡模式对应的参与因子排序Table 2 The order of participation factors corresponding to each oscillation mode

对各振荡模式的参与因子进行分析可知：

1)LFO模式主要是由D-PMSG的直驱风机轴系引发的，参与振荡子系统为D-PMSG轴系。

2)SSO-1、SSO-6是DFIG自身引发的，SSO-1主要受轴系与机侧控制器影响；SSO-6主要受DFIG转子磁链影响。参与振荡子系统分别为DFIG轴系与控制器、DFIG转子。

3)SSO-2与SSO-3两种模式是D-PMSG与柔性直流之间的交互作用而引发的，参与振荡子系统均为VSC-HVDC、D-PMSG控制器。

4)SSO-4模式是D-PMSG自身引发的，主要受机侧控制器影响，参与振荡子系统为D-PMSG。

5)SSO-5、SupSO模式是由柔性直流与DFIG送出交流输电线路交互引发的，参与振荡子系统均为DFIG、VSC-HVDC。

按照交直流系统来分，如表3所示。

2.2 时域仿真验证

在 PSCAD/EMTDC 环境下搭建如图1所示的模型，运行条件与2.1节相同。系统的仿真时长为10.0 s，当系统运行至2.0 s时，在受端电网公共连接点(point of common coupling,PCC)处施加一个时长为0.2 s的单相接地短路故障，观察母线PCC处输出有功功率的变化，其输出有功功率波形如图6所示。进一步地，对于所建立系统的输出有功功率，利用PRONY分析方法对其进行分析，结果如图7所示。

表3 模式分类Table 3 Mode classification

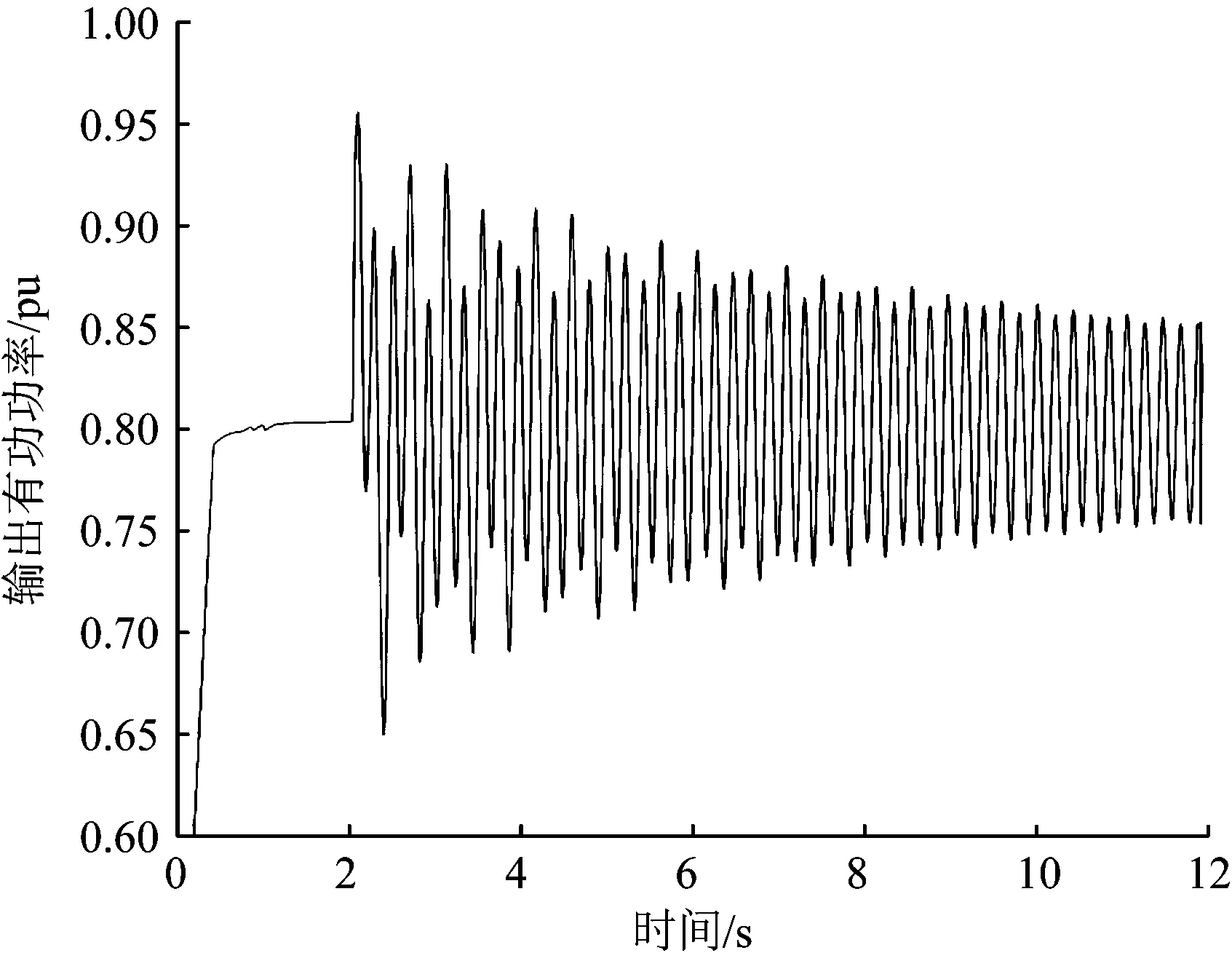
图6 有功功率振荡波形Fig.6 Waveform of active power oscillation

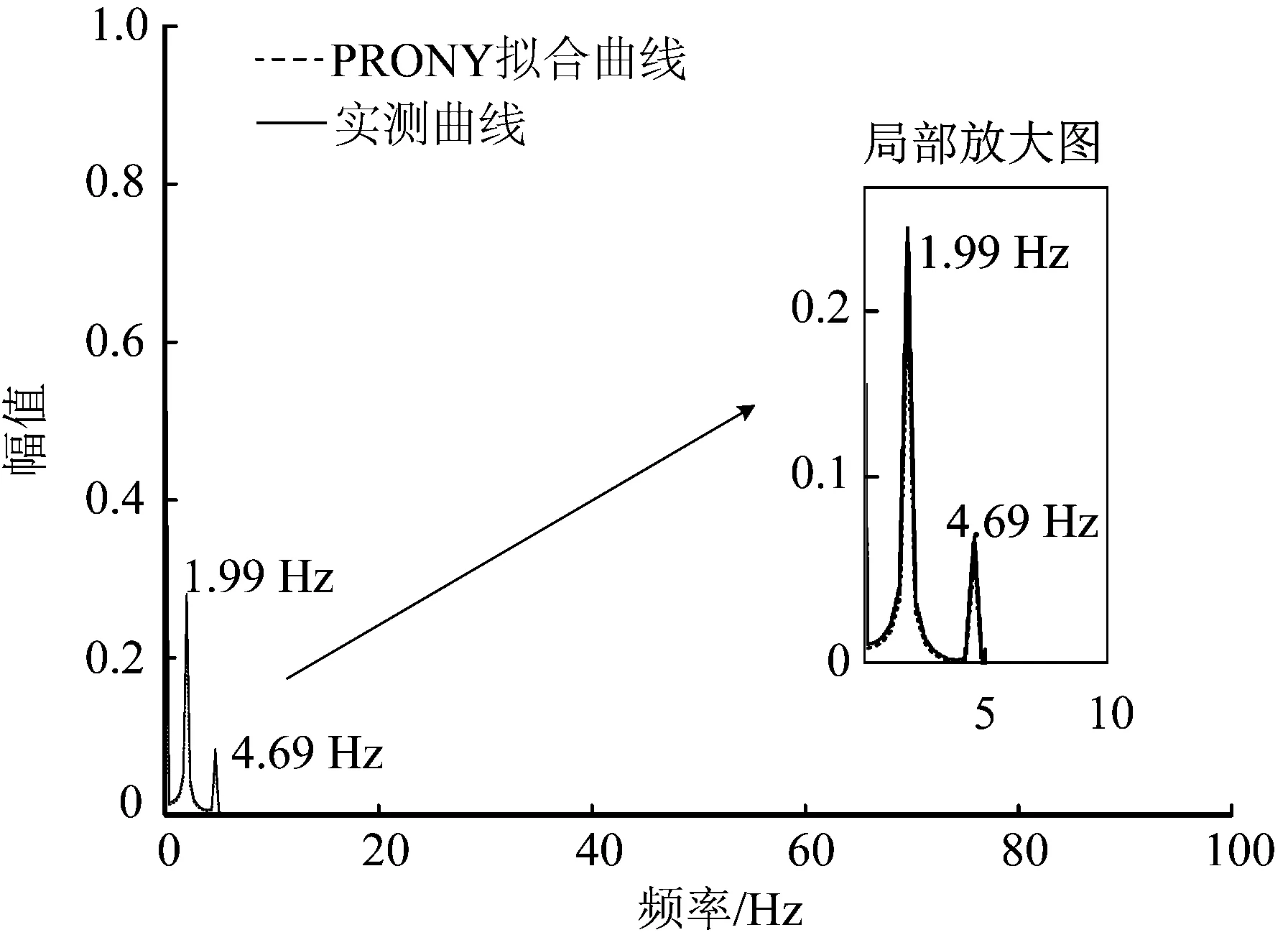
图7 PRONY分析得出的频谱图Fig.7 Spectrogram from PRONY analysis

由图6、7可知，输出有功功率频率成分包括1.99、4.69 Hz的次同步振荡分量，且1.99 Hz幅值较大。图7与表1结果一致，验证了文中所建模型的正确性。

3 系统参数影响分析

3.1 系统结构参数影响分析

由特征值分析结果可知，对风电场稳定性较为关键的结构参数有永磁直驱风电场并网容量、受端短路比等因素。下面从系统结构参数对交直流系统耦合振荡模式与耦合振荡模式两方面进行分析。

1)对交直流系统耦合振荡模式的影响。

将风电场并网容量由12 MW增加至240 MW、受端短路比由2增加至9，交直流系统固有振荡模式的阻频特性如图8、9所示。

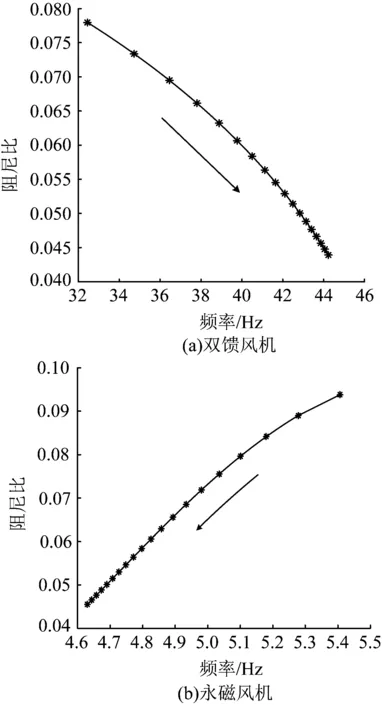
图8 风机并网容量对固有振荡模式的影响Fig.8 Effect of grid-connected capacity of wind power on inherent oscillation patterns

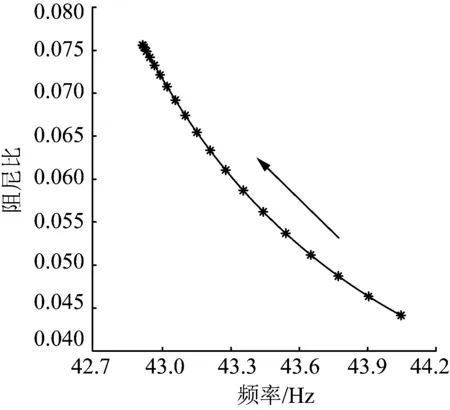
图9 系统短路比对固有振荡模式的影响Fig.9 Effect of SCR on the intrinsic oscillation mode

由图8、9可知风机并网容量的增加会降低系统固有振荡模式的阻尼比，短路比的增加会增加固有振荡模式的阻尼比。

为规避以上问题，实现住院药房系统与PIVAS系统的无缝对接，我院采用的是重新编写HIS系统自带的PIVAS模块，使其成为住院药房系统的下级系统，从而完成了PIVAS与住院药房一体化信息系统的构建。信息系统架构见图1。

2)对交直流系统耦合振荡模式的影响。

同样，将永磁直驱风电场并网容量由12 MW增加至240 MW、受端短路比由2增加至9。交直流系统耦合振荡模式的阻频特性如图10、11所示。

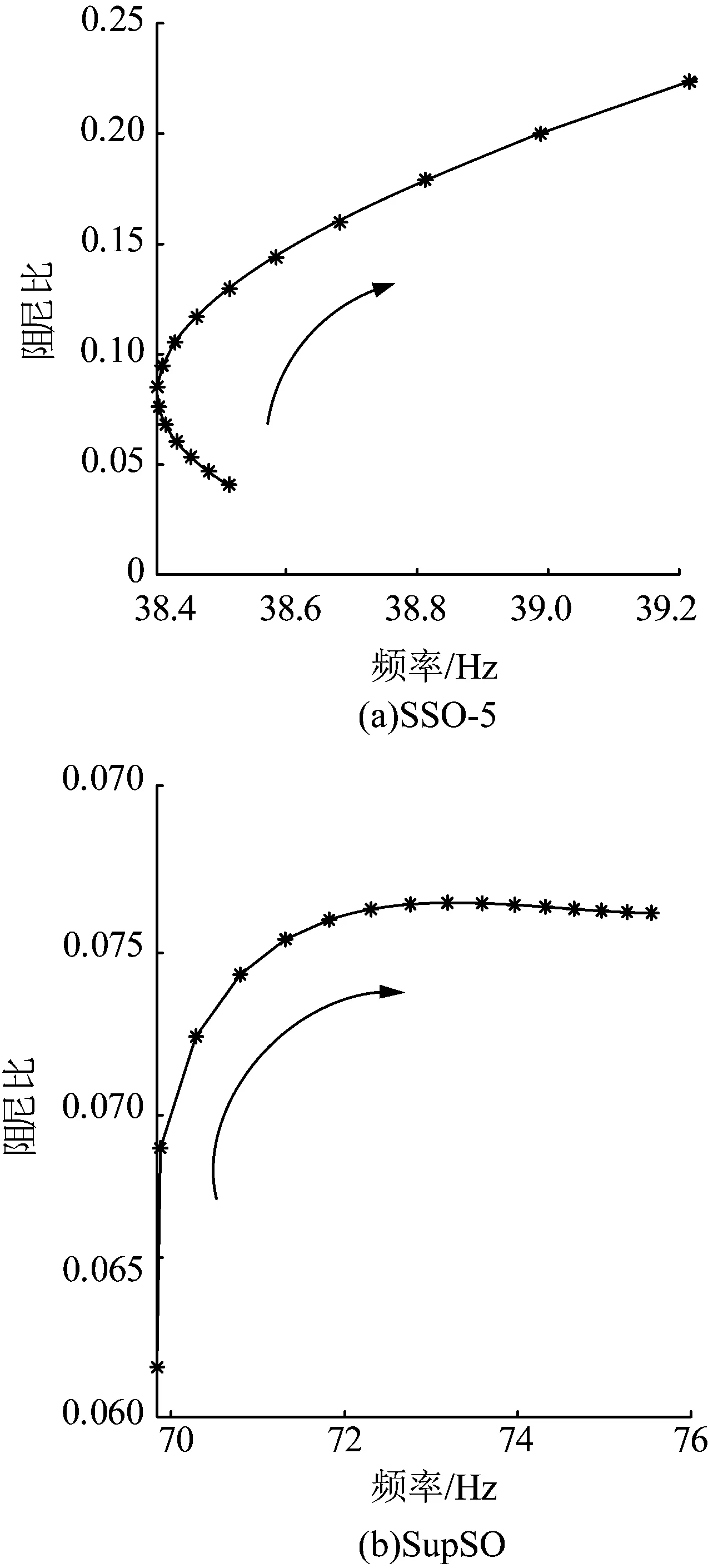
图10 受端电网短路比变化时耦合振荡模式阻频特性Fig.10 Damping frequency characteristics when the short-circuit ratio of the receiving-end power grid changes

由图8—11可以得到系统结构参数对SSO-5、SupSO两组耦合振荡模式以及固有振荡模式的影响。受端短路比SCR的增加同时改善了耦合振荡模式以及固有振荡模式的稳定性；风机并网容量的增加同时降低了耦合振荡模式以及固有振荡模式的稳定性。系统短路比越大，与之强相关振荡模式的阻尼比越大，电网稳定裕度越高。但是其改善的仅是与短路比自身强相关的振荡模式，与之无关的振荡模式无法通过提高SCR予以改善。

3.2 控制器参数影响分析

由特征值分析结果来看，系统所产生的振荡模式大多都与控制器参数相关，甚至有些模态同时受两个控制器影响。因此下文对控制器参数对交直流系统固有振荡模式与耦合振荡模式的影响进行分析。

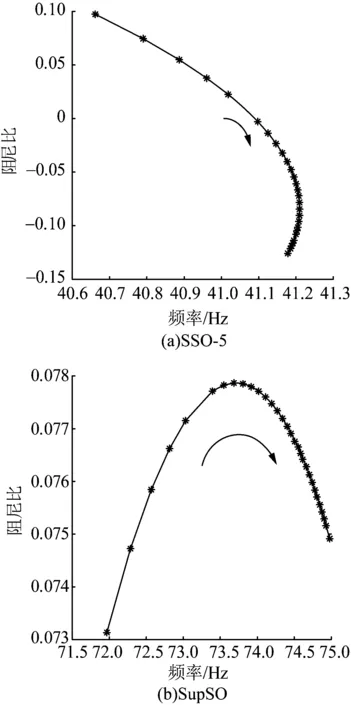
图11 并网风机容量变化时耦合振荡模式阻频特性Fig.11 Damping frequency characteristics when the capacity of grid-connected wind power changes

1)对交直流系统固有振荡模式的影响。

由参与因子可知，交流系统中固有振荡模式相关的控制器为双馈风机转子侧控制器。因此本节着重分析双馈风机控制器参数K1、K2，其阻频特性见图12。

2)对交直流系统耦合振荡模式的影响。

由参与因子排序可知，耦合振荡模式主要与柔性直流受端控制器参数有关，因此下文着重对柔性直流受端控制器参数cp1、ci1、cp2、ci2、cp3、ci3、cp4、ci4(cp1、ci1分别为送端控制器d轴外环比例系数、积分系数；cp2、ci2分别为送端控制器d轴内环比例系数、积分系数；cp3、ci3分别为送端控制器q轴外环比例系数、积分系数；cp4、ci4分别为送端控制器q轴内环比例系数、积分系数)进行分析。其控制器参数阻频特性见附录图A1—A4，具体影响规律如表5所示。

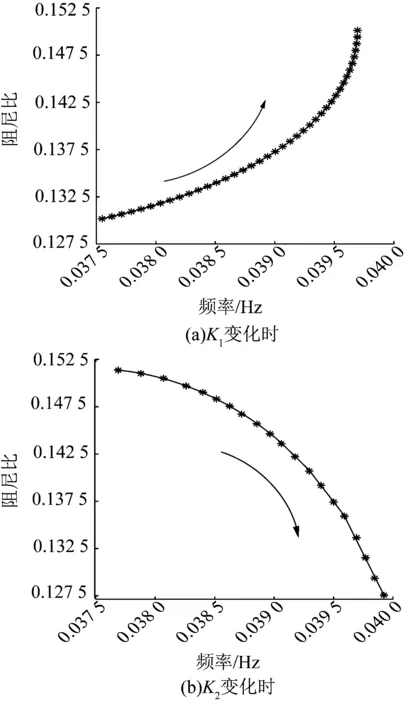
图12 双馈风机控制器参数K1、K2的阻频特性Fig.12 Frequency resistance characteristics of DFIG controller parameters K1 and K2

表4 直流系统控制器参数对固有振荡模式的影响Table 4 Effect of DC system controller parameters on inherent oscillation modes

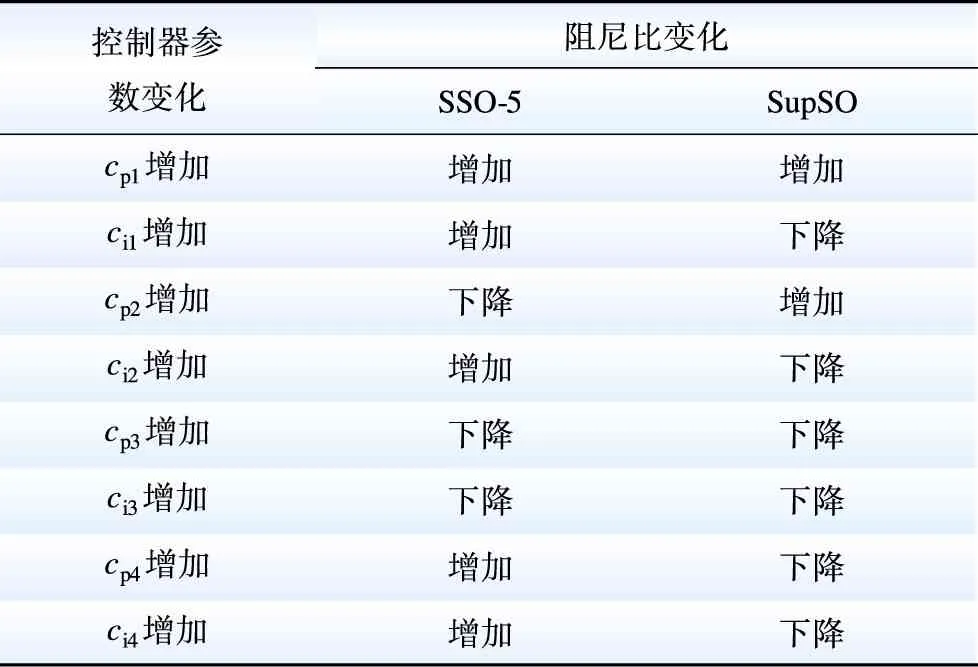
表5 系统结构参数对耦合振荡模式的影响Table 5 Influence of system structure parameters on coupled oscillation modes

结合以上分析可知：

1)cp1、cp3、ci3对两种模式的影响是趋同的，即：调节这些主导控制器参数，两种模式的阻尼比同向变化。

2)ci1、cp2、ci2、cp4、ci4对两种模式的影响是趋反的，即：调节这些主导控制器参数，两种模式的阻尼比反向变化。

3)SSO-4 与 SupSO 模式之间阻尼耦合的影响趋同与趋反均存在，因此有必要对VSC-HVDC控制器的参数(cp1、ci1、cp2、ci2、cp3、ci3、cp4、ci4)进行协调与优化，以及研究对应于系统渐进稳定的参数安全域。

3.3 系统参数影响结果对比

结合3.1节、3.2节可得到以下结论：

1)系统结构参数对交直流系统固有振荡模式与耦合振荡模式的影响规律相同。

2)控制器参数的比例系数对振荡模式的影响较大。

3)控制器参数对交直流系统耦合振荡模式影响较为复杂，难以得出明显结论。

4)风机控制器的比例系数(除K2外)与相应振荡模式均起到正相关作用。

4 直流系统与交流系统交互影响分析

分别使直流系统、交流系统初始参数与本文主要研究的交直流系统的直流部分、交流部分初始参数保持一致，分别对交流系统、直流系统以及两者之间的相互影响进行分析。

4.1 交流系统接入对直流系统的影响

交流系统接入前，风电场经直流系统并网的拓扑结构如图13所示。按照图1直流部分相同工况、参数进行特征值计算，其中参与因子排序中变化较大的振荡模式如表6所示。

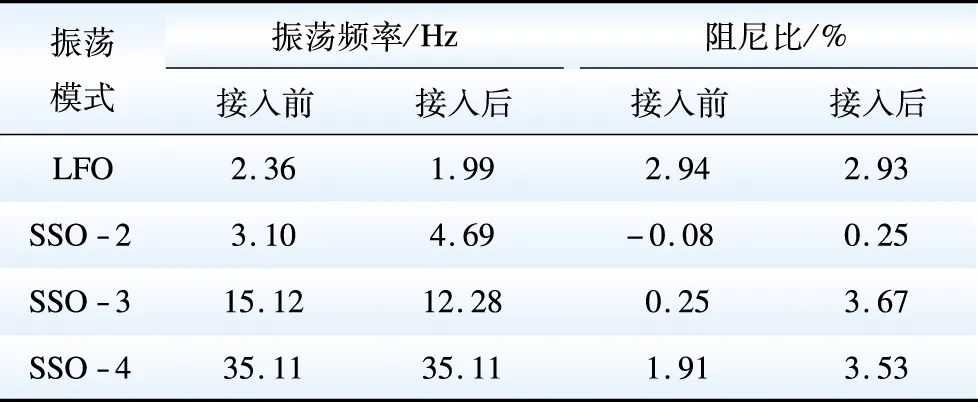
表6 交流系统接入前后直流系统的固有模态Table 6 Inherent modes of the DC system before and after the AC system connected

由表6对比可知，交流系统的接入使直流系统固有次同步振荡模式(SSO-2、SSO-3、SSO-4)的阻尼比上升，分别上升了0.33%、3.42% 与1.62%；使直流系统固有低频振荡模式LFO的阻尼比略有降低，减少了0.01%。因此，交流系统的接入有利于直流系统固有振荡模式的稳定。

4.2 直流系统接入对交流系统的影响

直流系统接入前，风电场经交流系统并网的拓扑结构如图14所示。

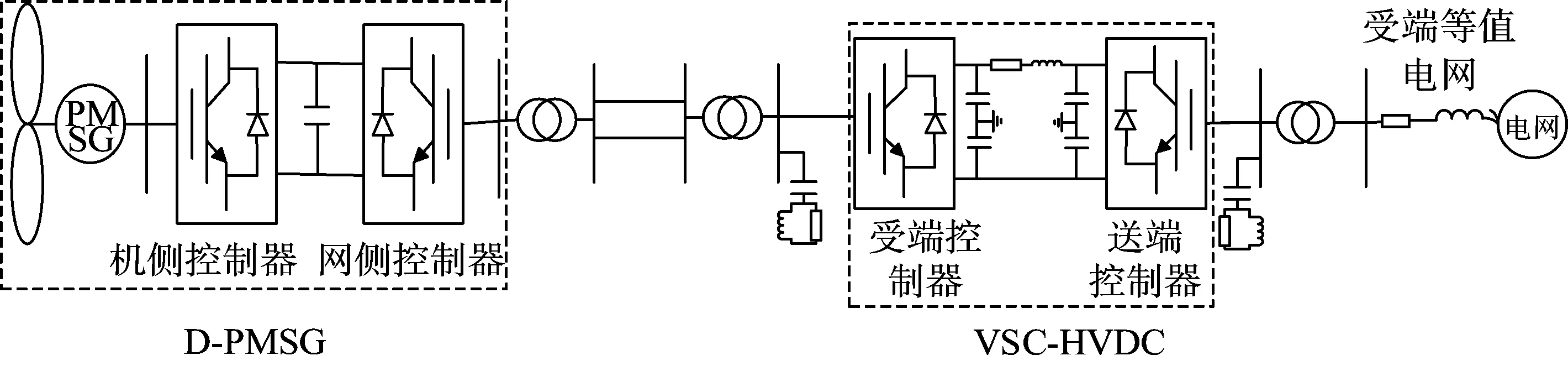
图13 永磁直驱风机经柔性直流并网Fig.13 PMSG grid-connected via flexible DC line

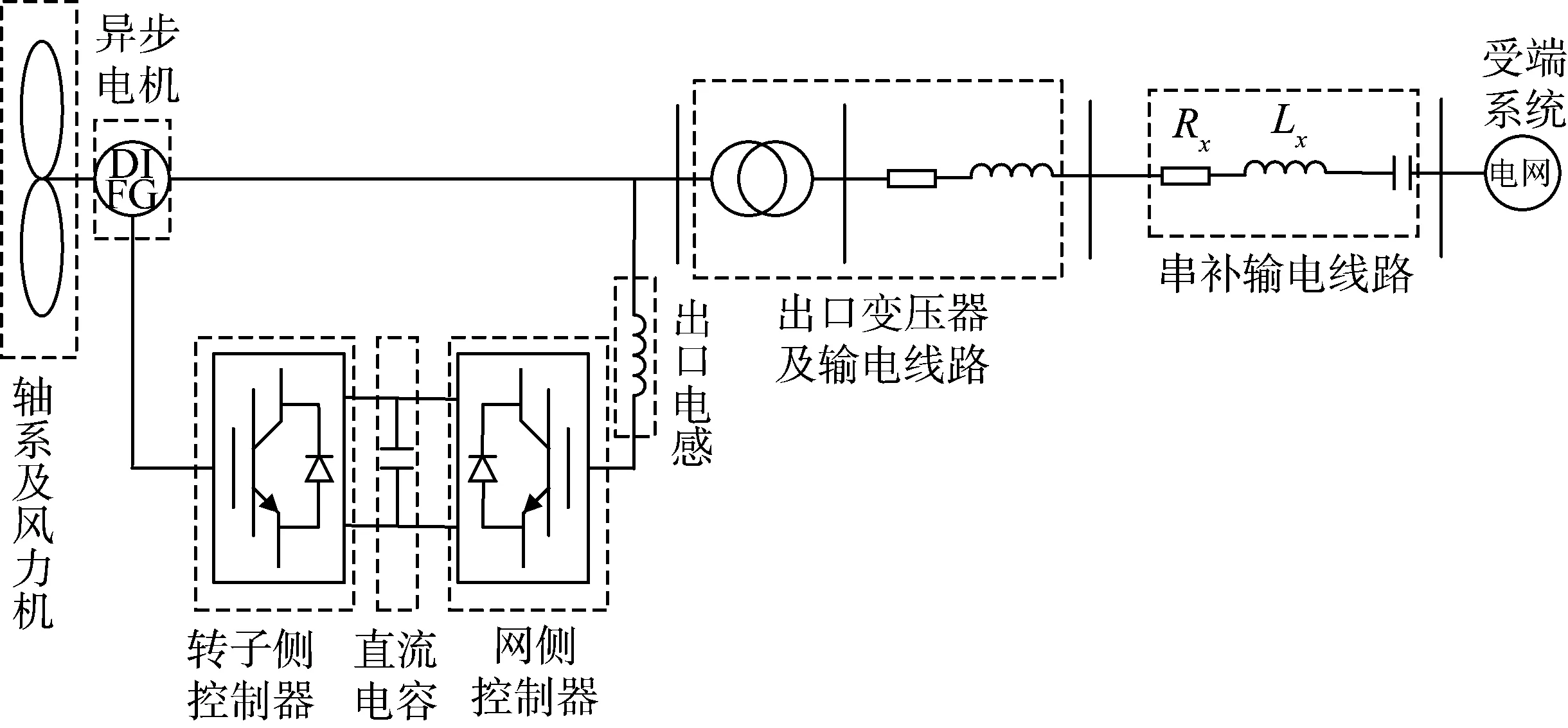
图14 双馈风机经交流并网拓扑Fig.14 DFIG grid-connected via AC lines

按照图1交流部分相同工况、参数进行特征值计算，其中参与因子排序中变化较大的振荡模式如表7所示。

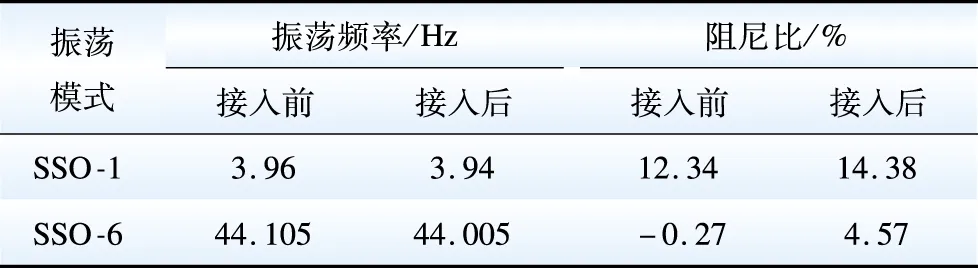
表7 直流系统接入前后交流系统的固有模态Table 7 Inherent mode of the AC system before and after the DC system connected

由表7可知，直流系统的接入使交流系统固有振荡模式(SSO-1、SSO-6)的阻尼比上升，分别上升了2.04%和4.84%。因此，直流系统的接入同样有利于交流系统固有振荡模式的稳定。

5 结 论

文中建立了风电场交直流接入系统的状态空间模型，利用特征值分析法研究了交直流场景下系统参数对振荡模式的影响以及交直流之间的交互影响。得到以下结论：

1)两系统的并联除了带来自身系统的固有振荡模式外，还因为交互影响产生了两组耦合振荡模式SSO-5与SupSO。且从交直流之间的交互影响来看，交流系统与直流系统均有利于提高对方固有振荡模式的阻尼比。

2)系统结构参数方面：无论对于耦合振荡模式还是交直流子系统固有振荡模式，受端SCR增加，与之强相关振荡模式的阻尼比越大，电网稳定裕度越高。但是其改善的仅是与短路比自身强相关的振荡模式，与之无关的振荡模式无法通过提高SCR予以改善；风机并网容量的增加大多数情况下会降低系统振荡模式的稳定性。

3)控制器参数影响方面：对于交直流子系统固有振荡模式，大多数情况下比例系数对系统振荡模式影响较大，提高比例系数有利于与其强相关振荡模式的稳定。对于交直流系统交互产生的耦合振荡模式，控制器参数对其的影响较为复杂，难以得出明显结论。

由上述分析可知，交直流系统之间耦合振荡模式往往具备更加复杂的特性。